Сумма углов четырёхугольника, вписанного в окружность: важные математические факты
На данной странице вы найдете подробную информацию о том, как рассчитывается сумма углов четырёхугольника, вписанного в окружность, а также полезные советы для решения задач, связанных с данной темой. Мы расскажем о геометрических особенностях таких четырёхугольников и о применении теорем для их анализа.
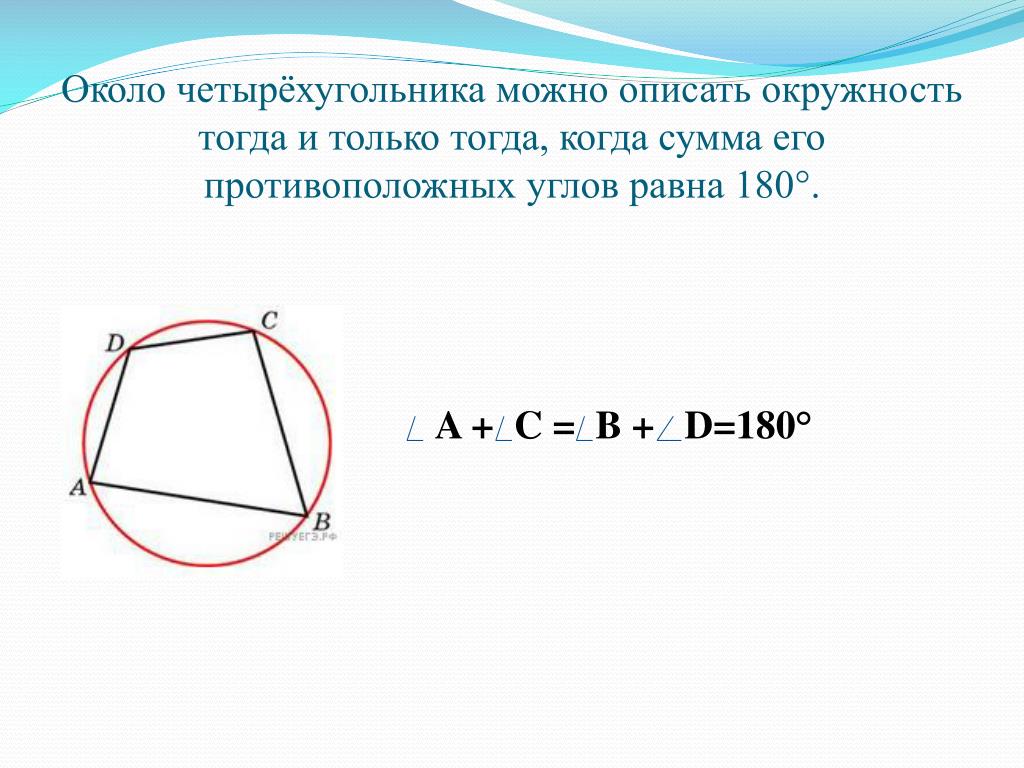


Помните, что сумма углов любого четырёхугольника, вписанного в окружность, всегда равна 360 градусам.
Нахождение угла четырехугольника

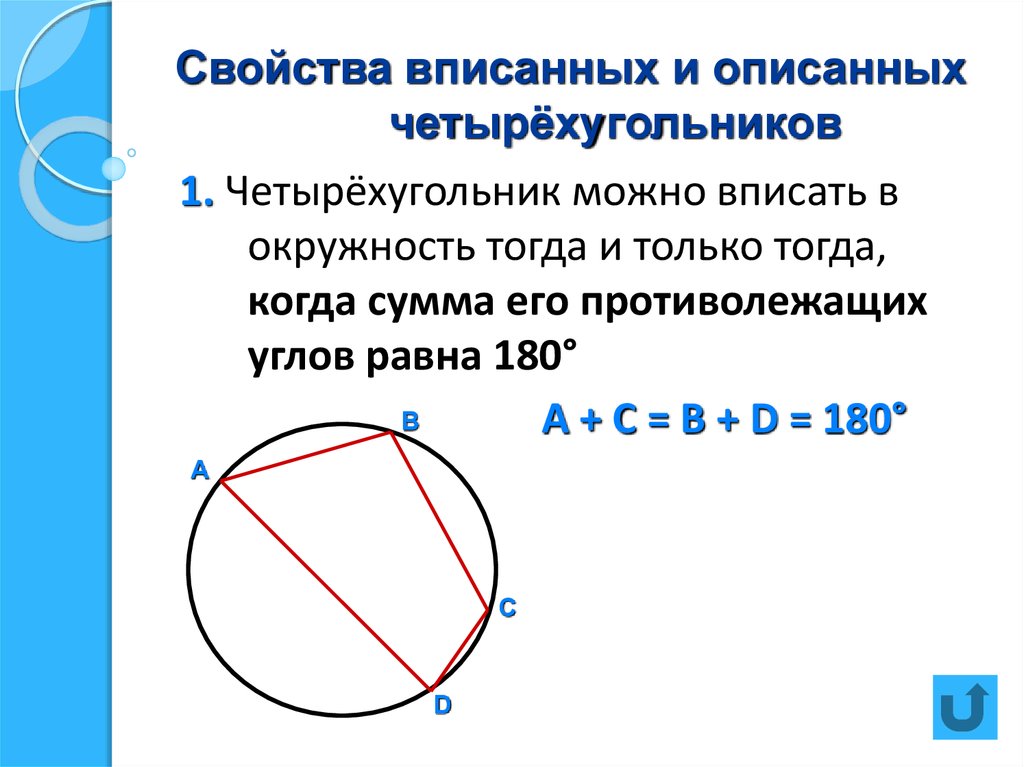
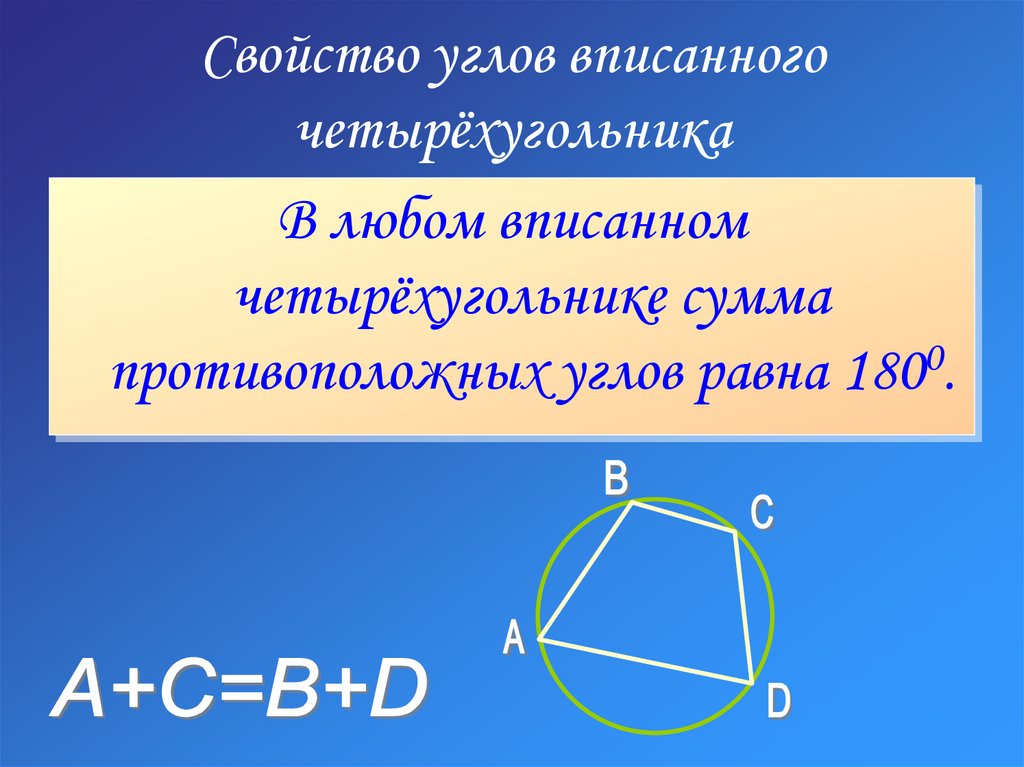
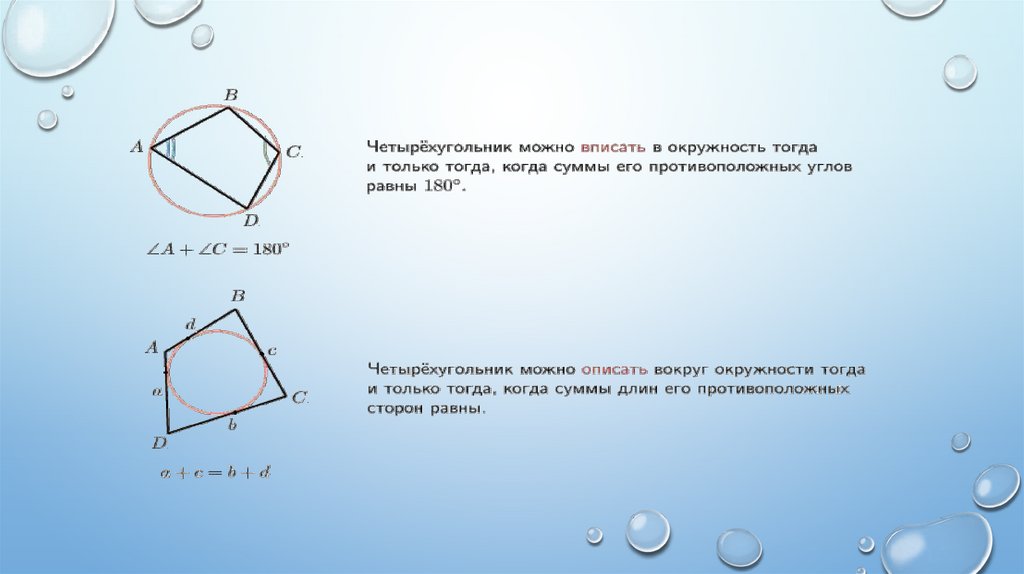
Важным свойством является то, что противоположные углы вписанного четырёхугольника всегда supplementary, то есть в сумме дают 180 градусов.

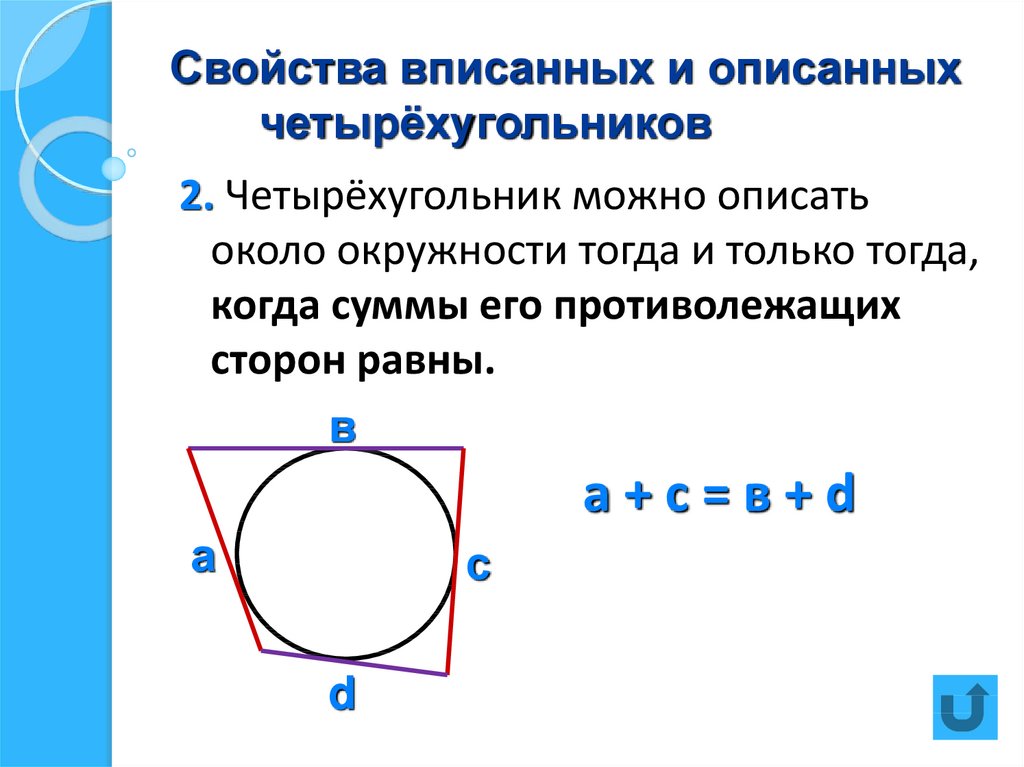
Геометрия Если в выпуклом четырехугольнике суммы противолежащих сторон равны, то в него можно
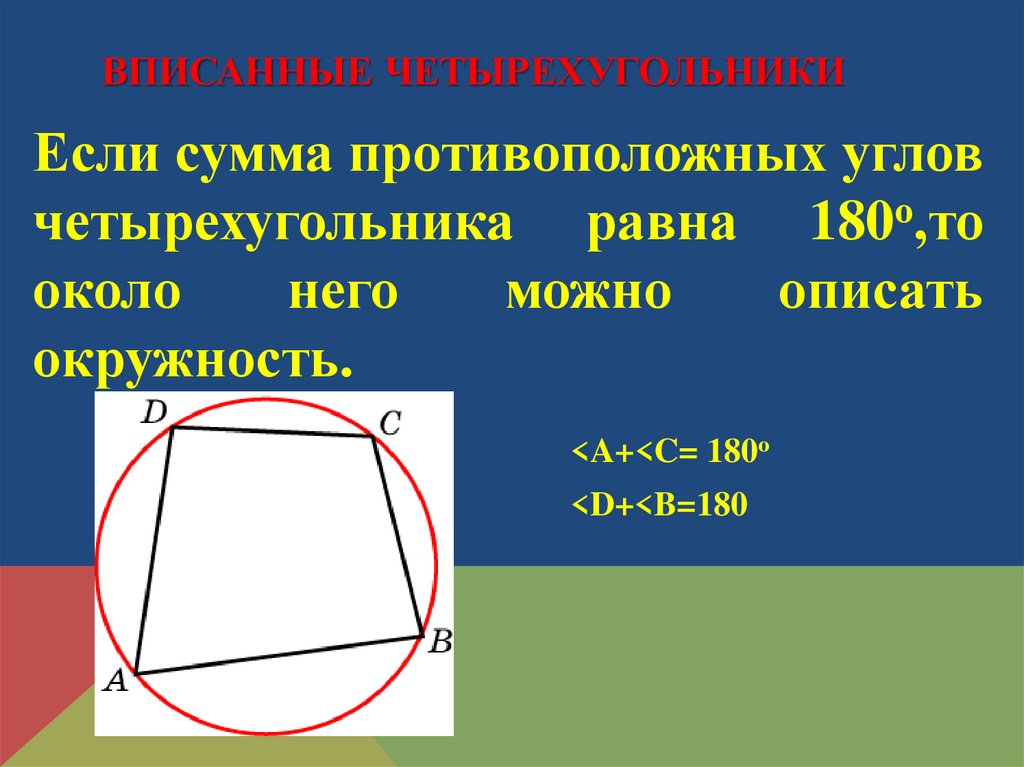
Для вычисления углов вписанного четырёхугольника можно использовать теорему о сумме противоположных углов.

Вписанные и описанные окружности. Вебинар - Математика
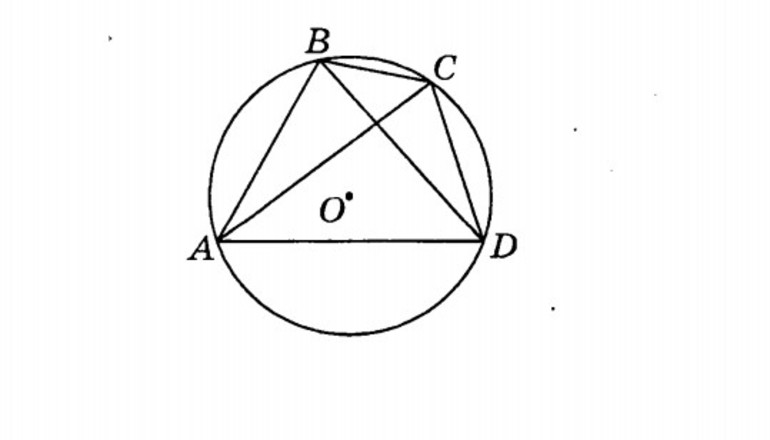

Обратите внимание, что углы, образованные двумя секущими окружности, также могут быть связаны с углами вписанного четырёхугольника.

Угол А вписанного четырёхугольника ABCD равен
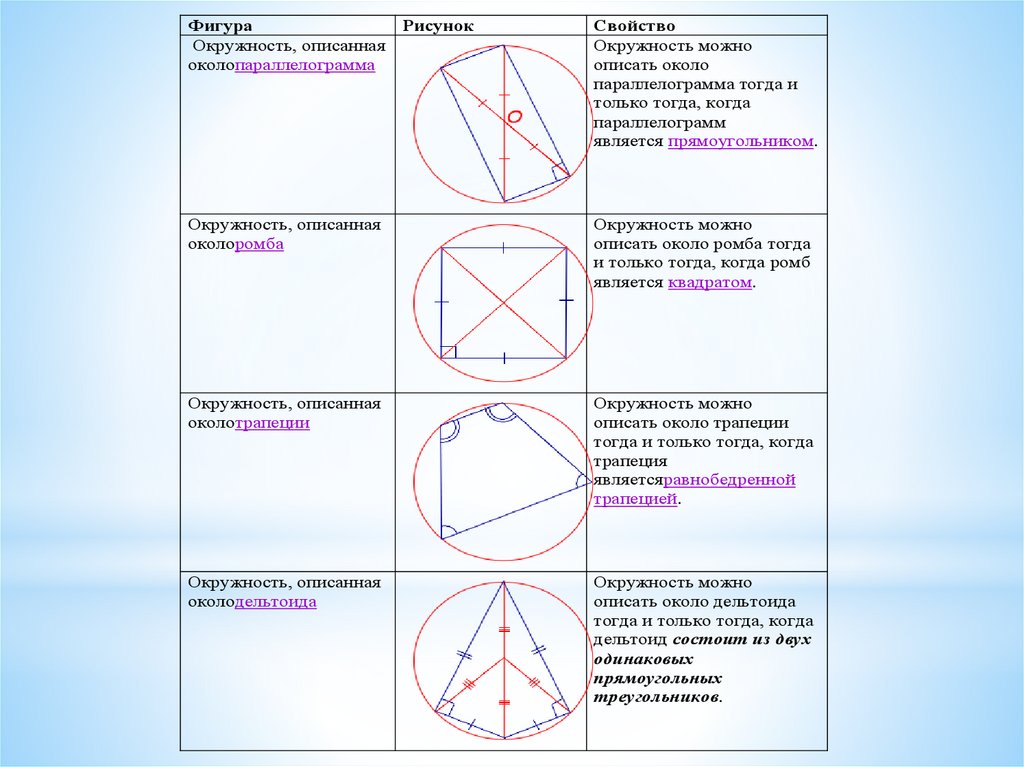
Если два противоположных угла равны, это может указывать на симметричность четырёхугольника относительно центра окружности.

Геометрия Если четырехугольник является вписанным в окружность, то сумма его противолежащих углов


Для нахождения углов в задачах используйте известные теоремы о вписанных углах и свойствах окружности.

Задачи на вписанные углы часто решаются через анализ геометрических зависимостей и использование теоремы о внешнем угле.
Использование круговой симметрии может помочь в решении сложных задач, связанных с четырёхугольниками, вписанными в окружность.

угол a четырёхугольника abcd вписанного в окружность равен 46
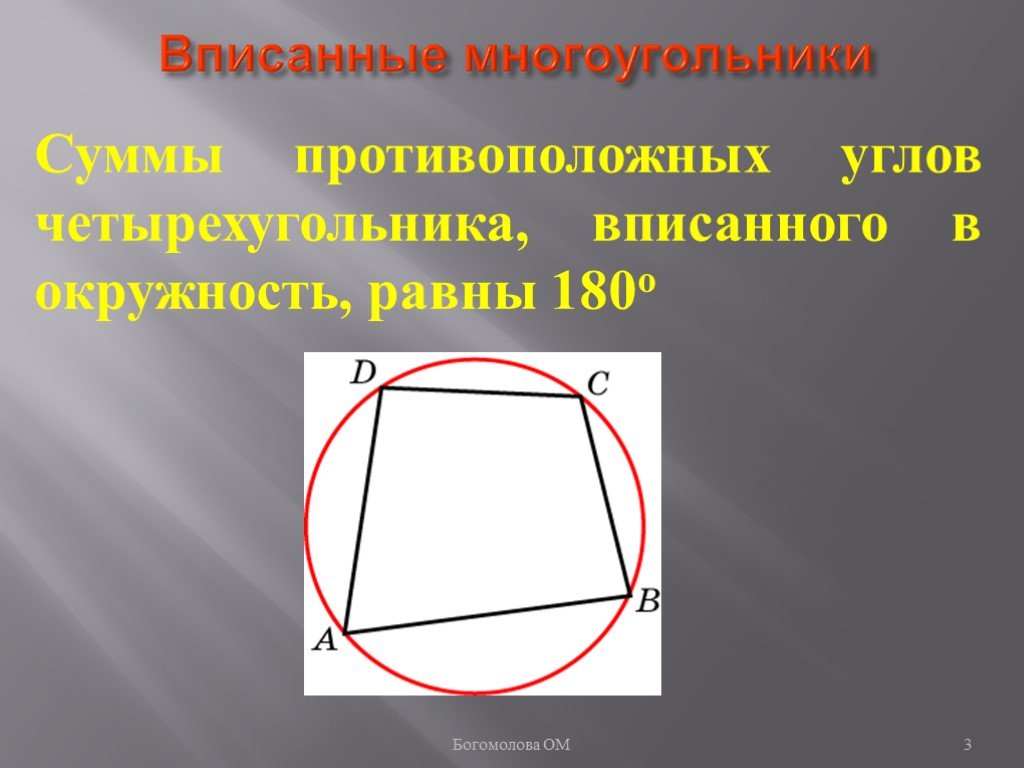
При решении задач обращайте внимание на равенство углов в параллельных и пересекающихся секущих.
Для точных вычислений углов используйте формулы для углов, образующихся в различных точках окружности, и не забывайте о дополнительных теоремах, таких как теорема о внешнем угле.
