Уравнение плоскости: основные принципы и примеры
На этой странице вы найдете подборку фотографий и полезных советов по составлению уравнения плоскости, используя заданную точку и нормальный вектор, а также подробное объяснение каждого этапа.

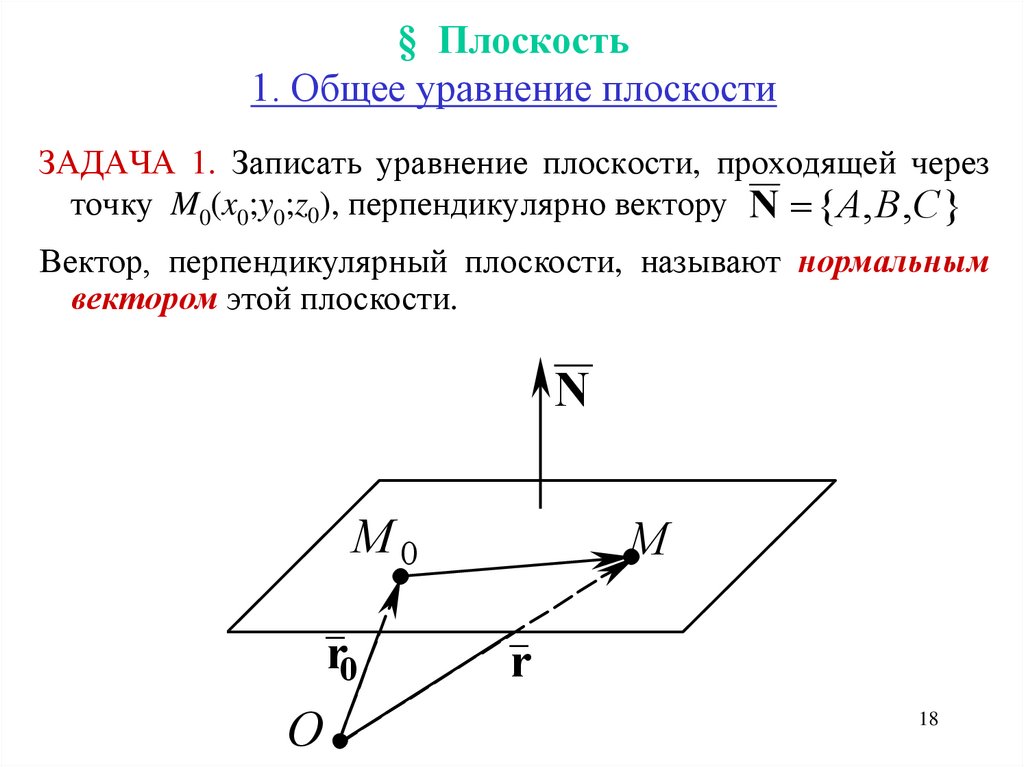
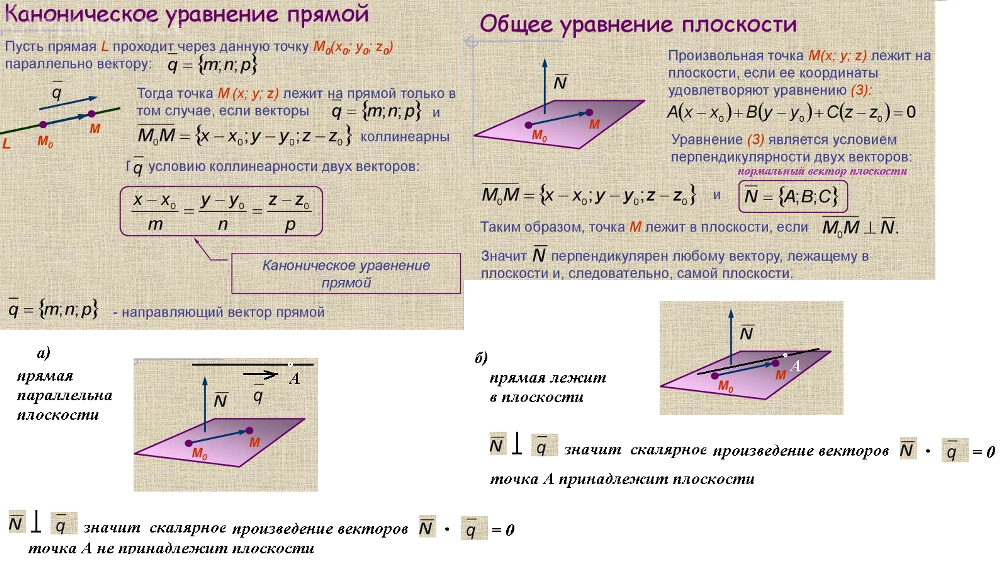
Всегда начинайте с записи координат точки, через которую проходит плоскость.

Уравнение плоскости через 2 точки параллельно вектору

Определите компоненты нормального вектора для построения уравнения.

Уравнение плоскости через точку и нормаль

Используйте общее уравнение плоскости: Ax + By + Cz + D = 0.
4 серия \

Подставьте координаты точки в уравнение для нахождения параметра D.

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примеры
Убедитесь, что коэффициенты A, B, C соответствуют компонентам нормального вектора.
Математика Без Ху%!ни. Касательная плоскость и нормаль к поверхности.


Для проверки уравнения подставьте координаты других точек на плоскости.
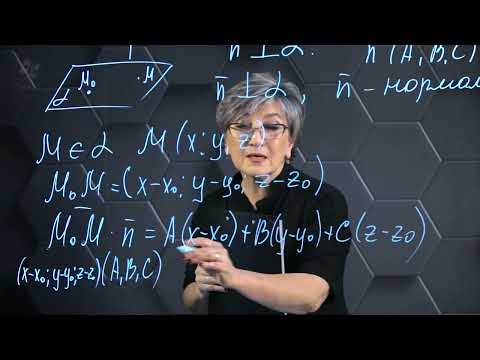
Уравнение плоскости. 11 класс.
Помните, что нормальный вектор определяет ориентацию плоскости в пространстве.

Используйте скалярное произведение для дополнительной проверки правильности.
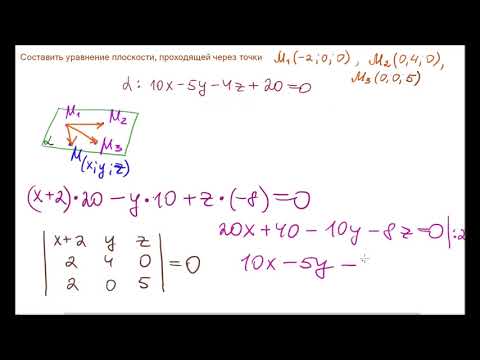
Уравнение плоскости через 3 точки


При визуализации уравнения плоскости используйте 3D-графики.


Не забывайте учитывать единицы измерения координат и вектора.
Устная задача с собеседования в МФТИ

