Основы и полезные советы по изучению тригонометрии
Тригонометрические функции – ключевые инструменты математики, применимые в архитектуре, инженерии и физике. Здесь вы найдете полезные советы и визуальные примеры.
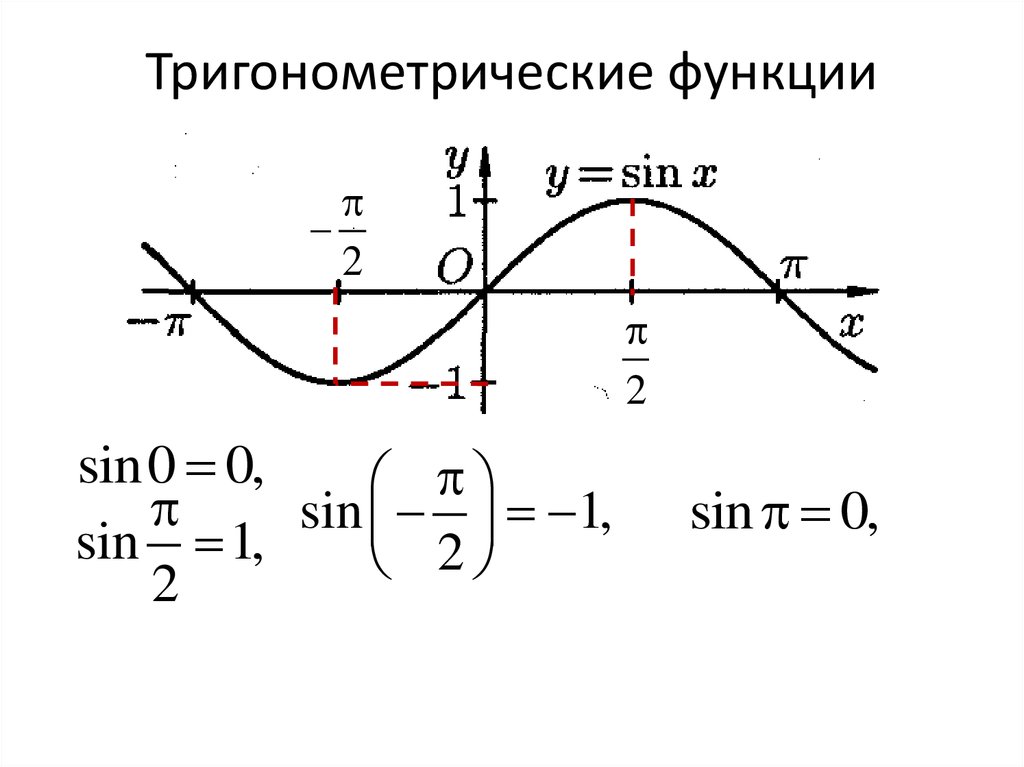
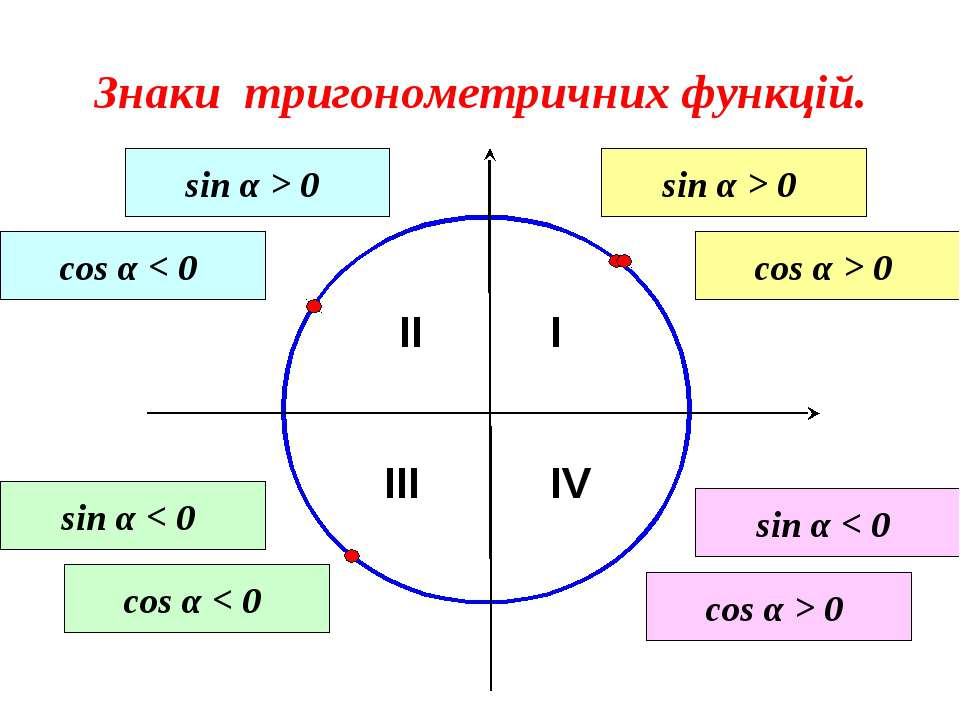
Начните изучение с понимания основных функций: синуса, косинуса и тангенса.

Форсунка для ГТУ Газпром #shorts #росмолд #3дпечать #3дпринтер #импортозамещение #завод #турбина


Запомните основные значения тригонометрических функций для углов 0°, 30°, 45°, 60° и 90°.
Внутримышечная гематома в н/3 передней брюшной стенки справа, размерами 5.3х5.9 мм.
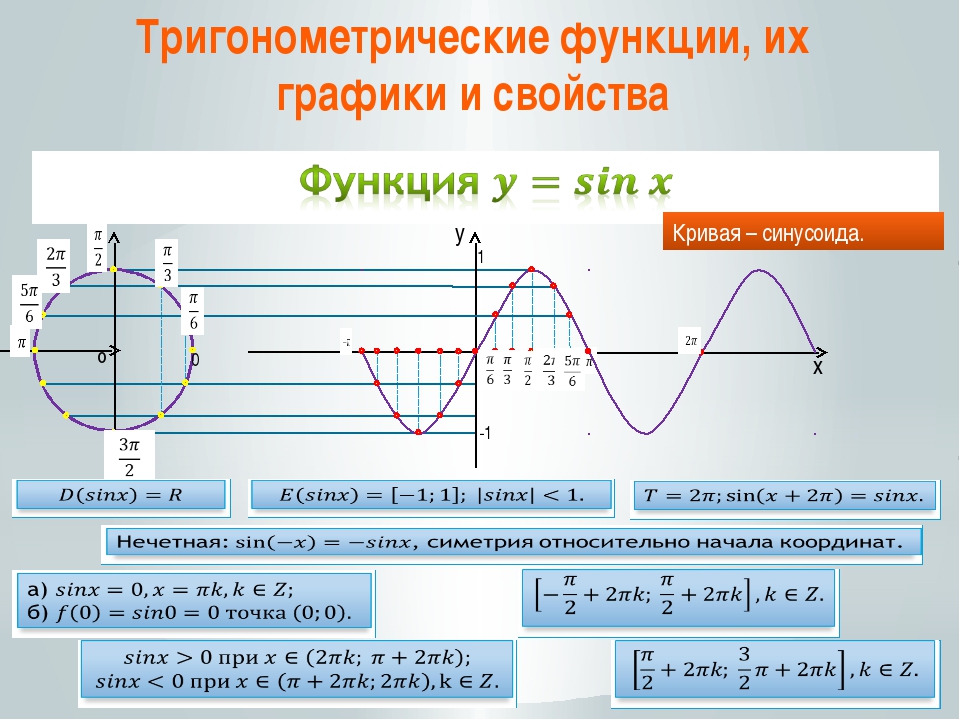
Используйте окружность на координатной плоскости для визуального понимания функций.

Ежегодные соревнование на трициклах в Норвегии😱😨😳

Тренируйтесь решать уравнения с тригонометрическими функциями, начиная с простых примеров.

Функции подвижного цилиндра и манометр у пресса. #гидравлика
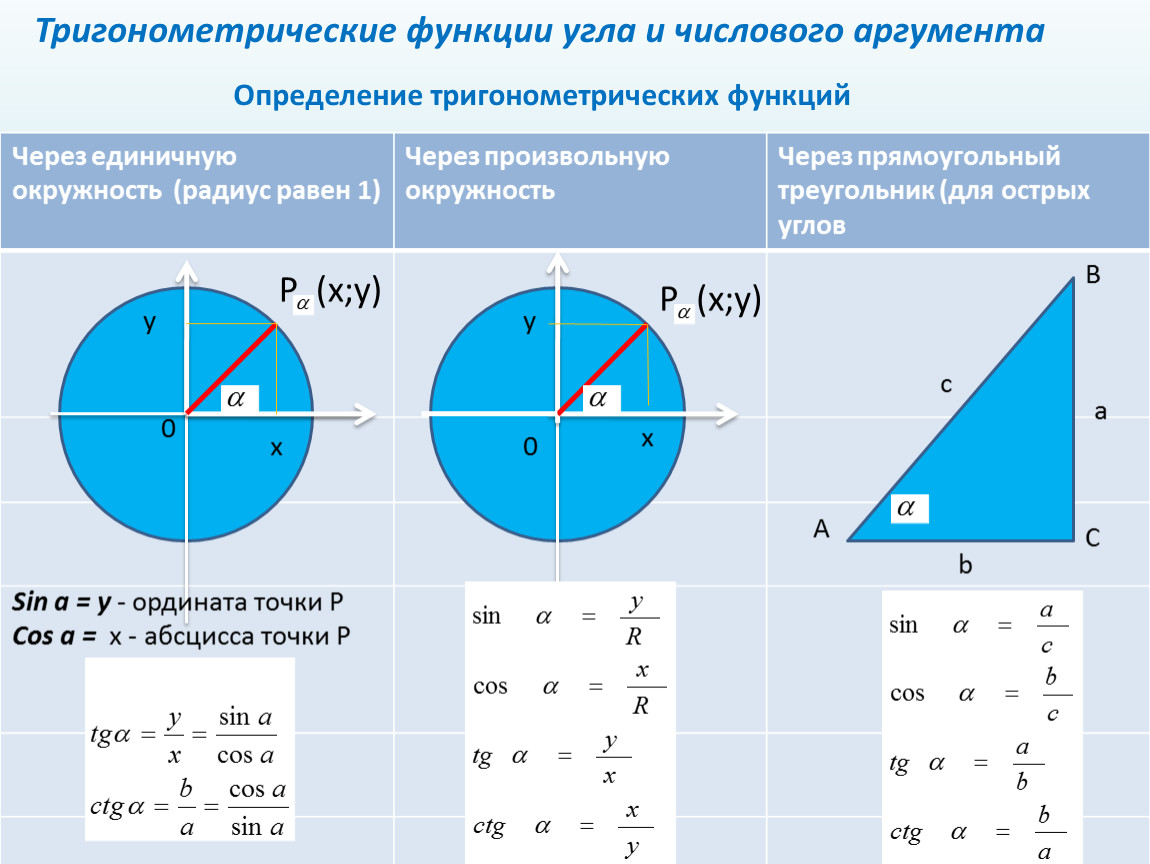
Попробуйте использовать графики, чтобы понять поведение функций на интервале.

Лучшая прокладка гбц


Регулярно решайте задачи на практическое применение тригонометрии, например, расчет высоты объекта или длины тени.

Тротуарная плитка , разница колормикс и однотонной
Изучите формулы приведения для упрощения вычислений в различных квадрантах.

Обратите внимание на связи между тригонометрическими функциями, такие как основное тригонометрическое тождество.

Практикуйтесь с помощью интерактивных симуляций или приложений для построения графиков.

Не забывайте повторять пройденный материал, чтобы закрепить знания.

Пластины большого по размерам плоского конденсатора расположены горизонтально - №

