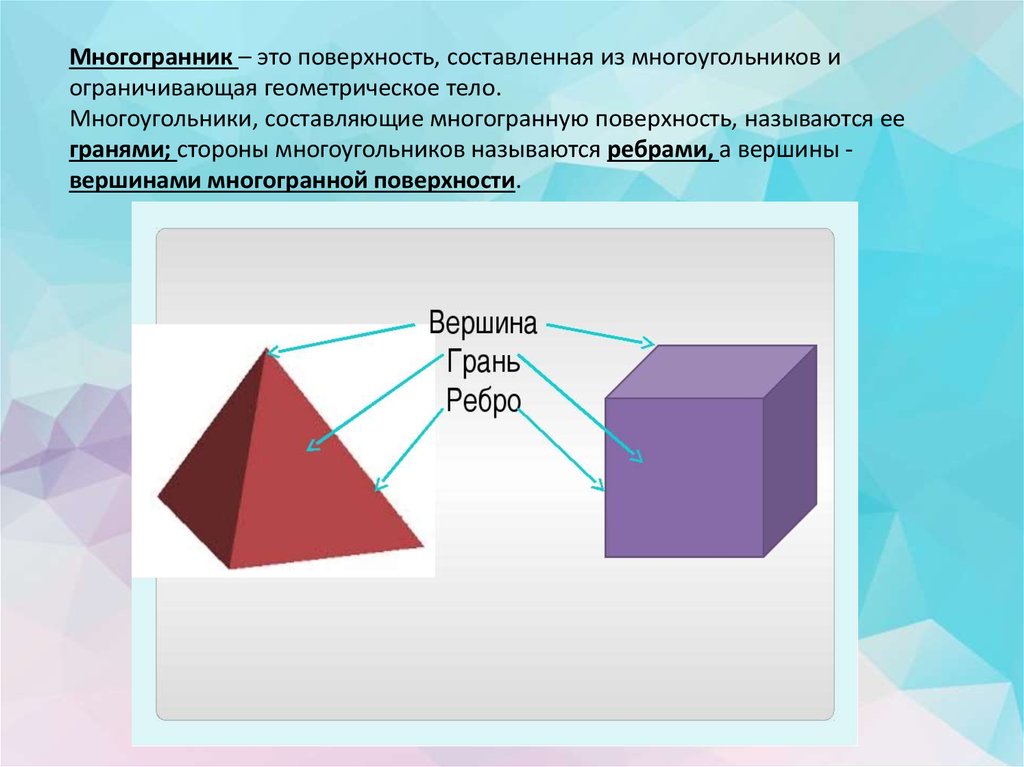
Важность понимания граней, ребер и вершин в многоугольниках для создания точных геометрических фигур
На этой странице мы собрали полезные советы и фотографии, которые помогут вам лучше понять основные геометрические понятия, такие как многоугольники, их грани, ребра и вершины. Эти знания важны для создания различных фигур и решения задач в области геометрии. Изучайте практические рекомендации и применяйте их для улучшения ваших навыков.
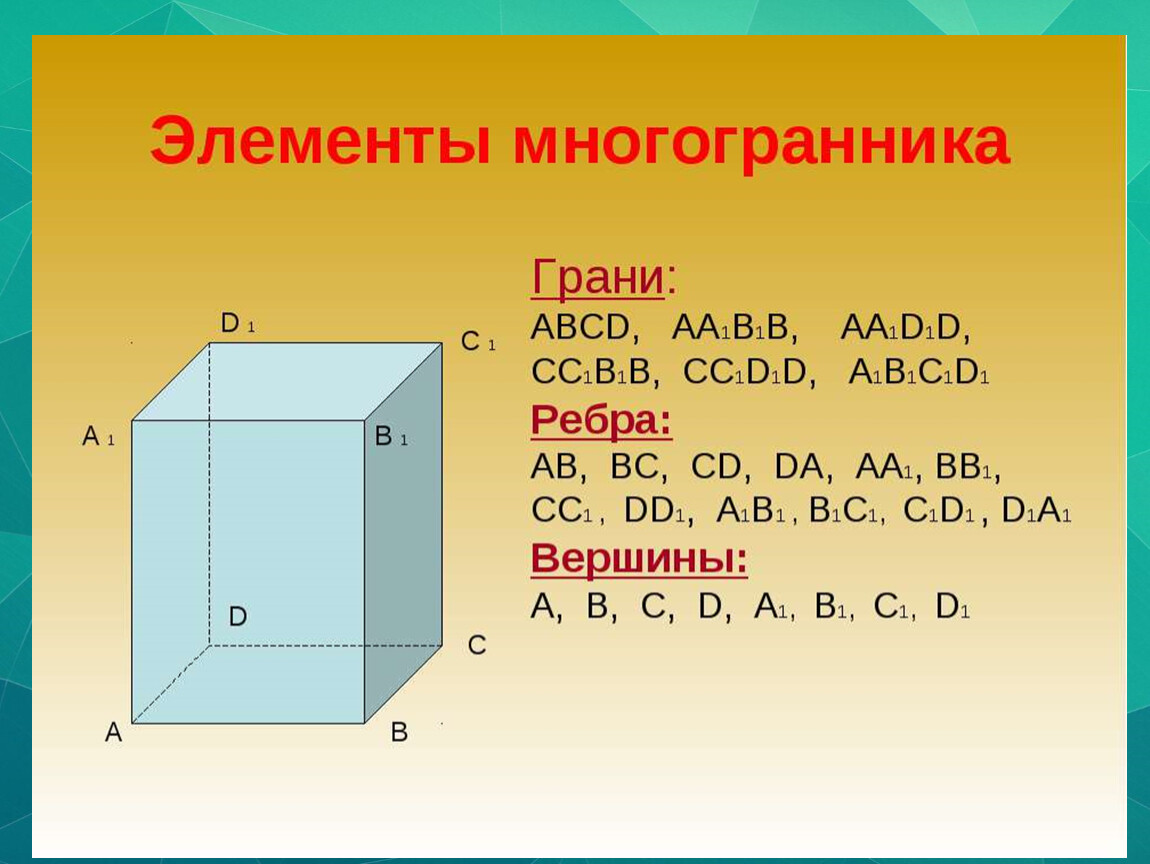
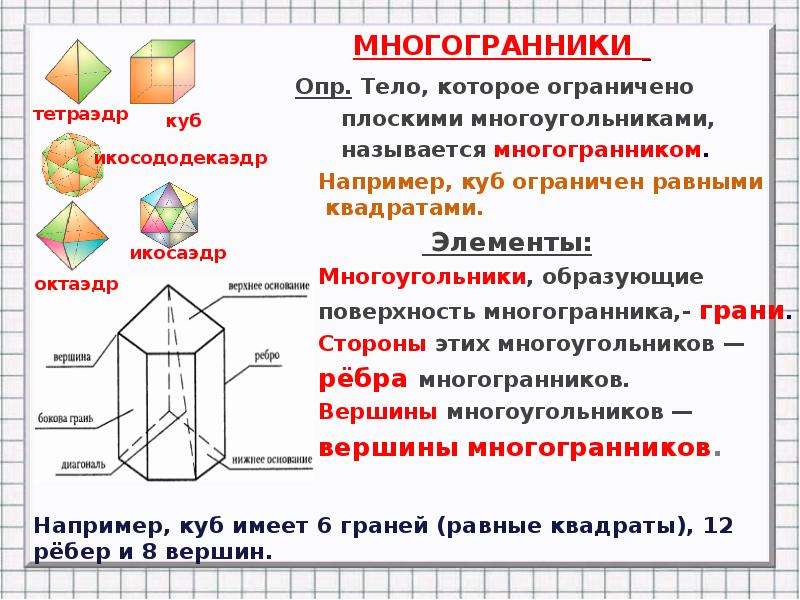
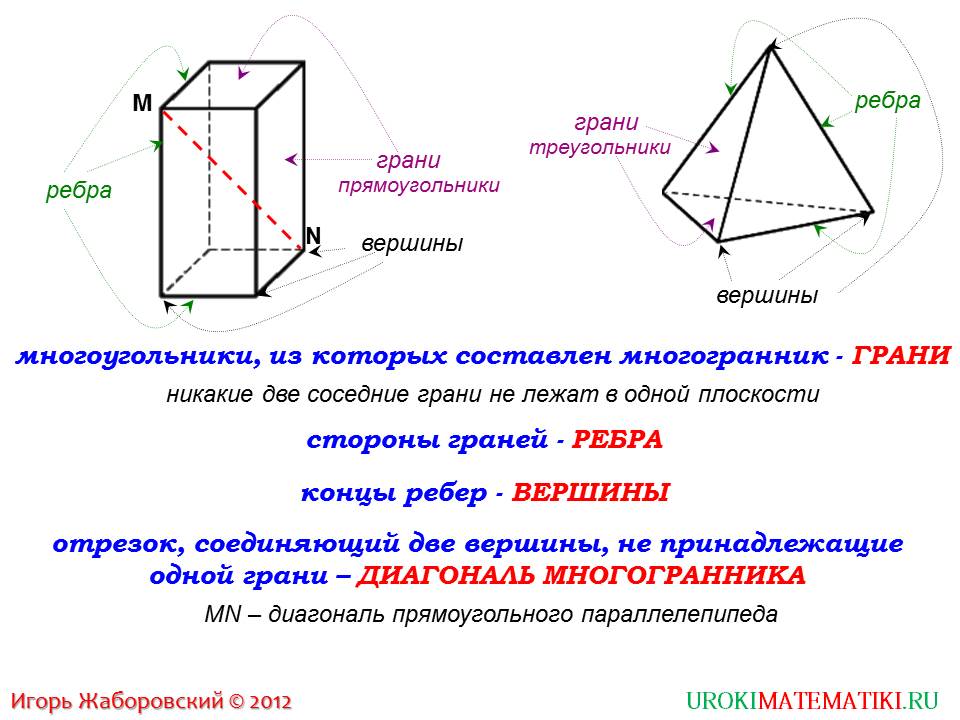
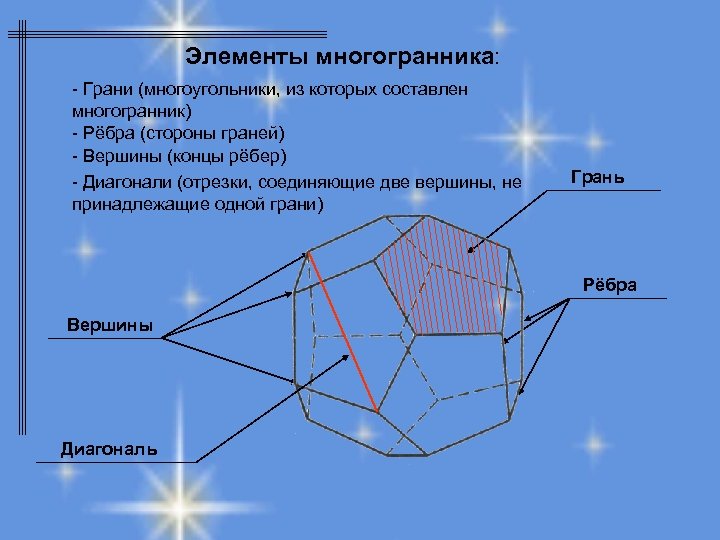
Перед началом работы с многоугольниками важно четко понимать, что такое грани, ребра и вершины, чтобы правильно построить фигуру.

Видеоурок по математике \
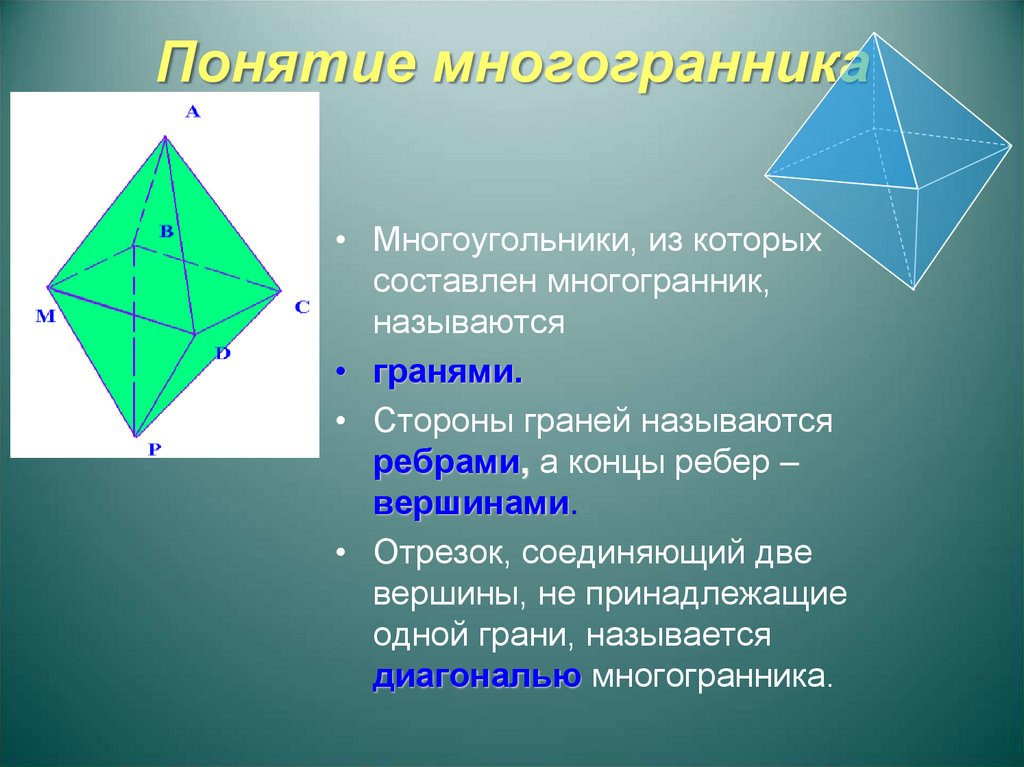
Каждая грань многоугольника представляет собой плоскую поверхность, а количество граней зависит от количества сторон у многоугольника.

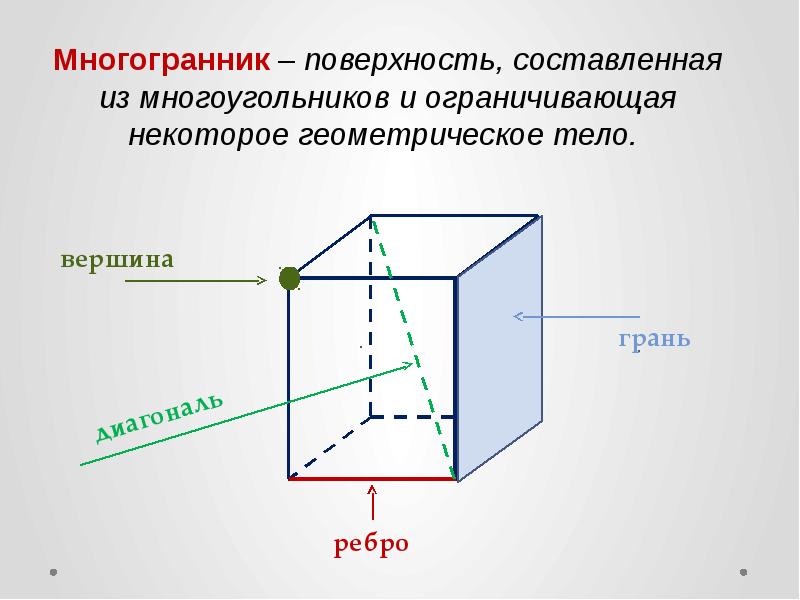
Геометрия 10 класс. Понятие многогранника
Ребра многоугольника — это линии, соединяющие соседние вершины, и их количество всегда на единицу меньше, чем количество граней.

Интересный способ изготовления многогранников (без сварки)
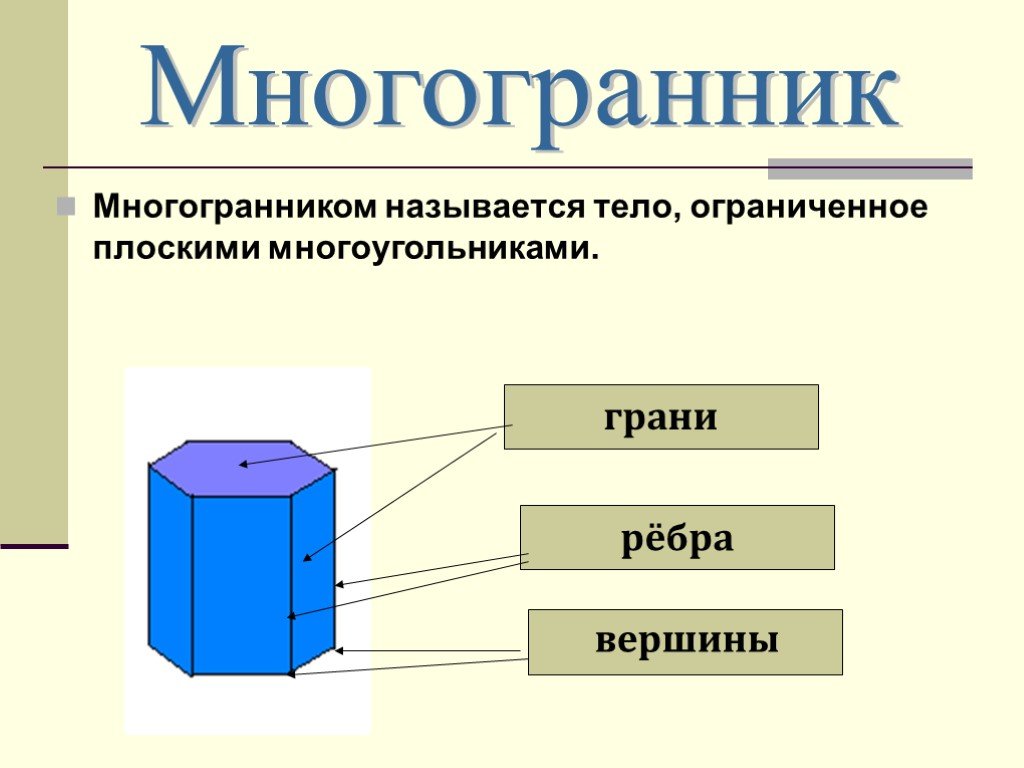
Вершины многоугольника — это точки, в которых пересекаются два ребра, и их количество всегда равно количеству углов в многоугольнике.

ВЕРШИНЫ И СТОРОНЫ МНОГОУГОЛЬНИКА
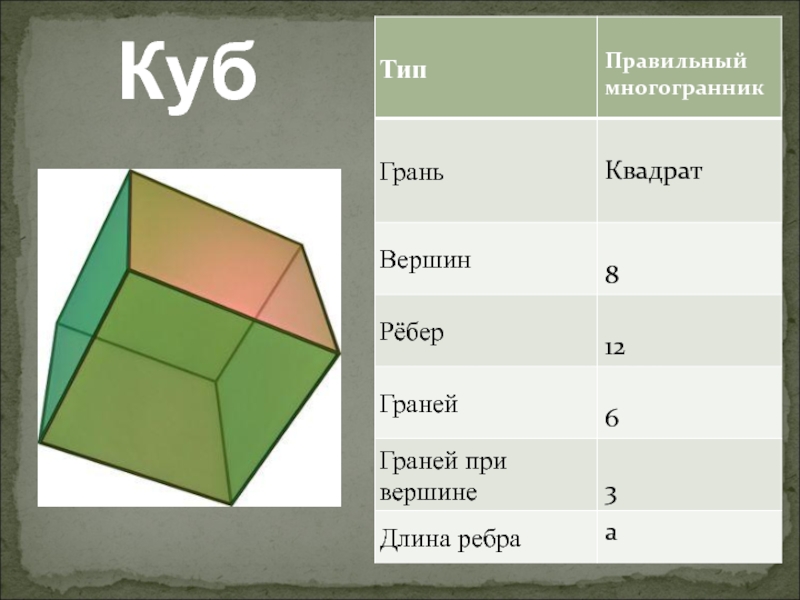
Чтобы построить правильный многоугольник, начните с правильных вычислений для каждого угла и длины сторон.

Как найти площадь многогранника за минуту
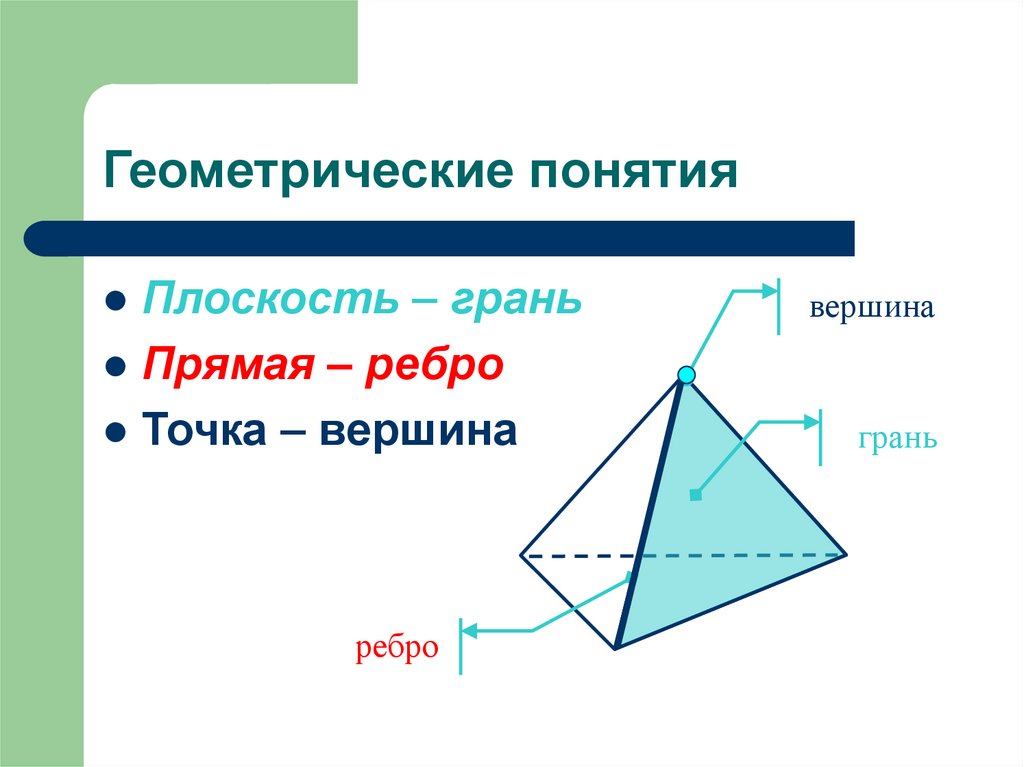
Использование геометрических инструментов, таких как линейки и транспортира, поможет точнее определить и построить каждую грань и ребро.
Если вы работаете с трехмерными многоугольниками, важно учитывать взаимное расположение граней, чтобы не нарушить форму.

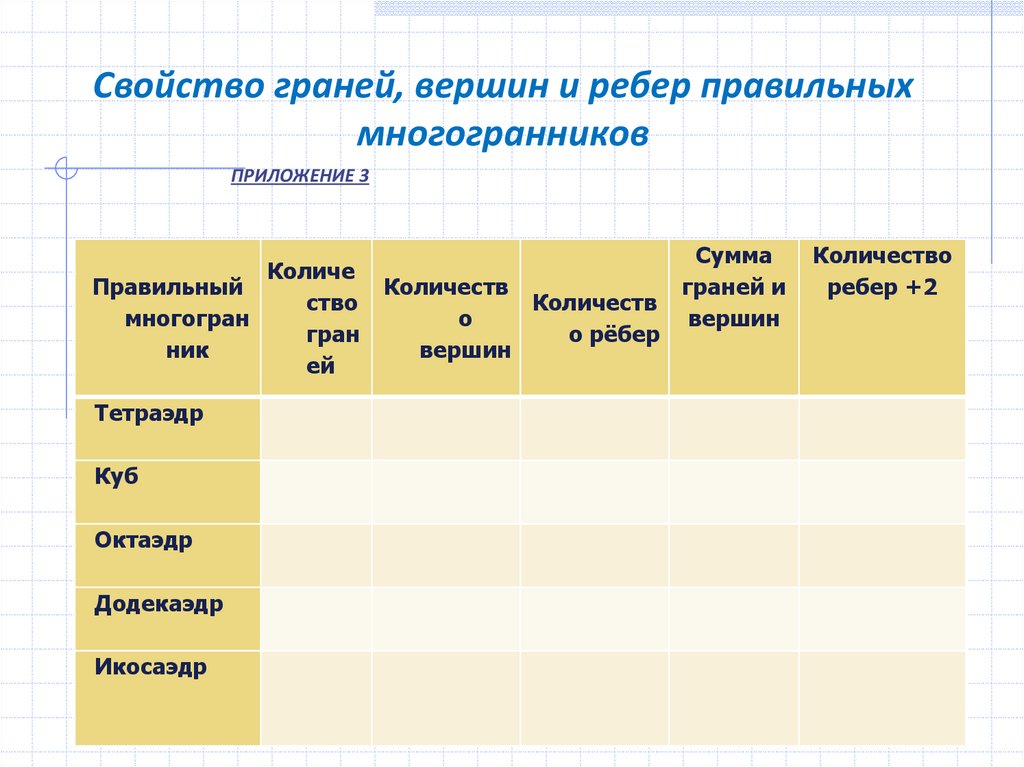
Задача. Сколько вершин граней и ребер у многогранника?

Часто для сложных фигур применяется метод декомпозиции: разделение на более простые многоугольники помогает лучше понять структуру.

М1365. Многогранник, где нельзя отметить рёбра, чтобы у каждой грани было чётное число отмеченных

20 Грани, рёбра и вершины куба
Геометрические программы и приложения могут быть полезны для моделирования многоугольников и их изучения на практике.

Тайны многогранников
Помните, что изучение многоугольников важно не только в математике, но и в архитектуре, инженерии и дизайне, где эти принципы активно применяются.