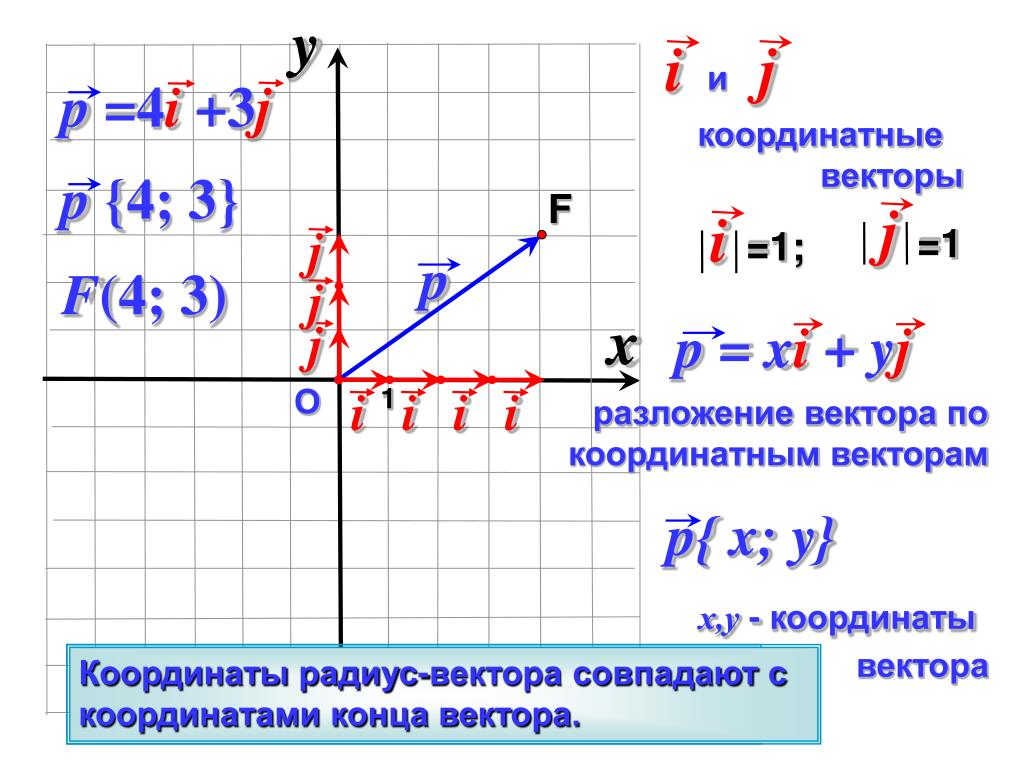
Основные принципы координат вектора и их использование в математике и физике
Координаты вектора являются важной составляющей при работе с векторами в различных областях науки и техники. Правильное определение координат вектора помогает точно описать его положение и направление в пространстве, что важно как для решения теоретических задач, так и для практических приложений. В этом разделе мы рассмотрим, что такое координаты вектора, как их находить и правильно интерпретировать.

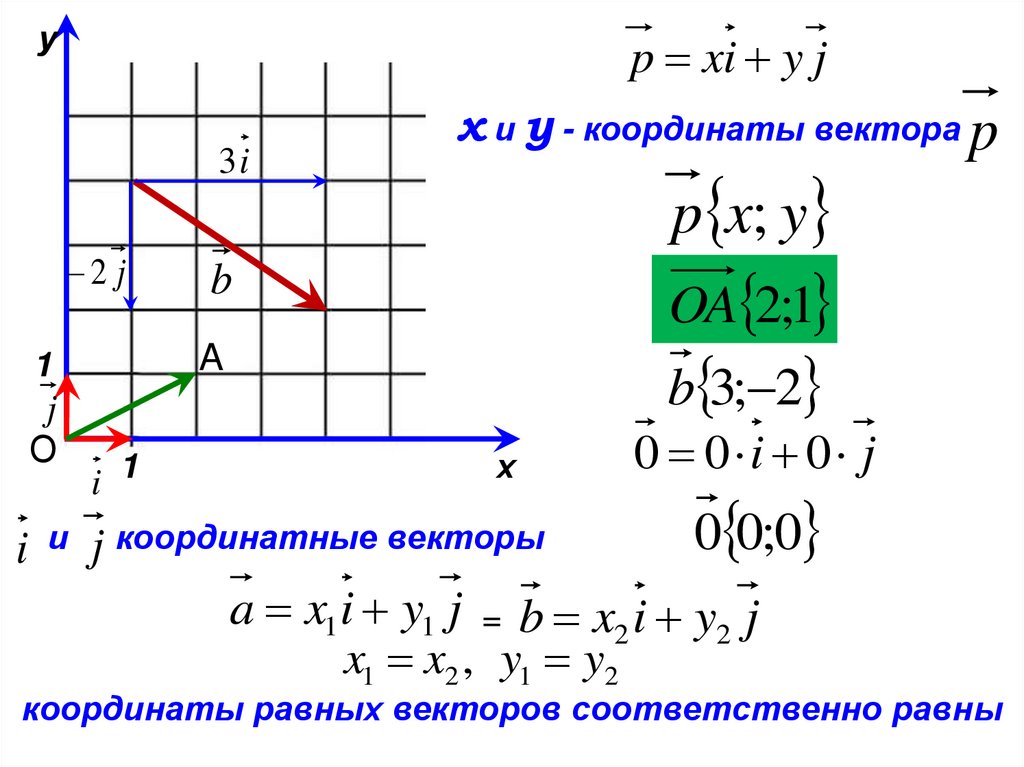
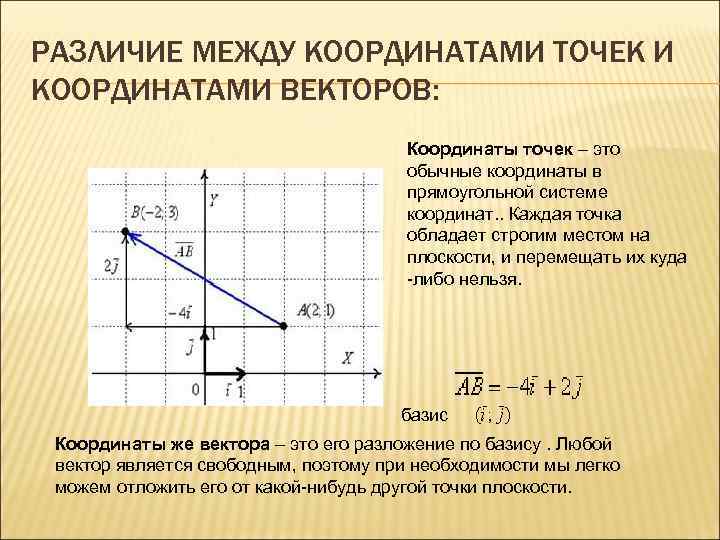
Для определения координат вектора в двумерной системе координат достаточно знать его проекции на оси X и Y.

Координаты вектора - Геометрия 7-9 класс #86 - Инфоурок

Вектор можно представить как разницу между двумя точками в пространстве, где координаты этих точек будут исходными данными.
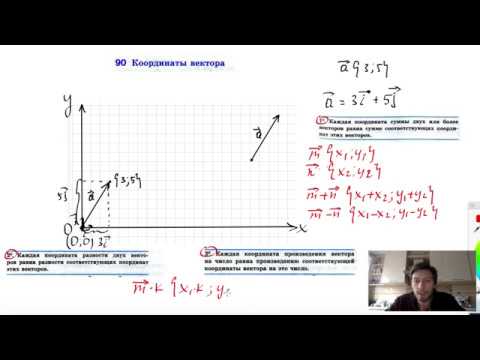
90. Координаты вектора
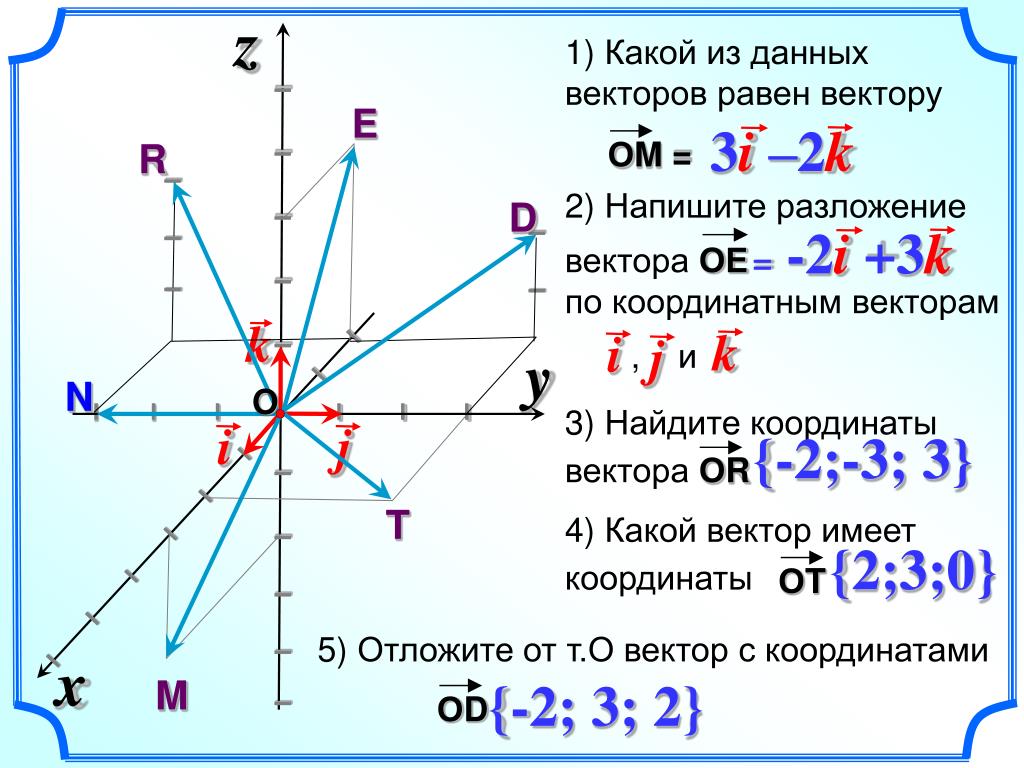
При работе с векторами в трехмерном пространстве, не забывайте, что для их описания требуется три координаты: X, Y и Z.

ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)
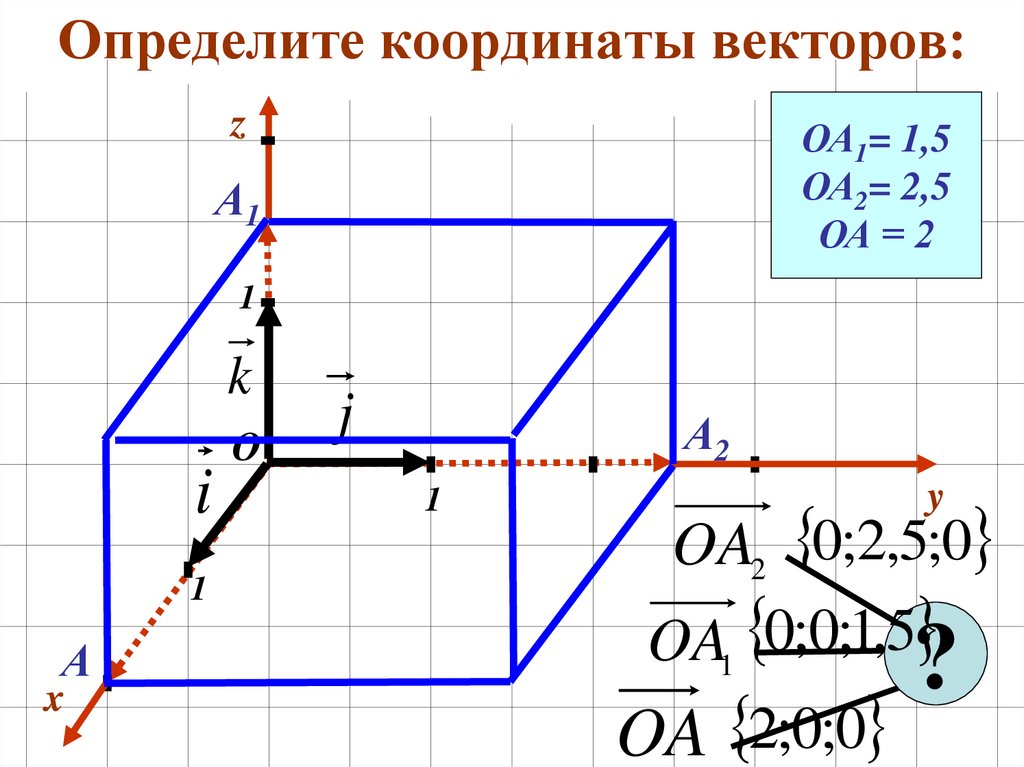

Если вектор лежит на одной из осей, то его координаты будут иметь вид (x, 0) или (0, y) в двумерном пространстве.

Понятие вектора. Координаты вектора. Коллинеарность

Если вектор перпендикулярен осям, его координаты могут быть представлены через углы и длину с использованием тригонометрических функций.

Понятие вектора. Коллинеарные вектора. 9 класс.


Для нахождения координат вектора на плоскости можно воспользоваться формулами, основанными на геометрии, например, через угол между вектором и осями.

Когда вектор задан с использованием углов и величины, его координаты можно вычислить, умножив длину на косинус или синус угла относительно каждой оси.
Векторы с одинаковыми координатами носят название «коллинеарных» и могут быть преобразованы друг в друга через масштабирование.

ГЕОМЕТРИЯ 9 класс: Координаты векторов
Если вам нужно найти координаты вектора в пространстве, важно помнить, что любой вектор можно разложить на компоненты по осям координатной сетки.
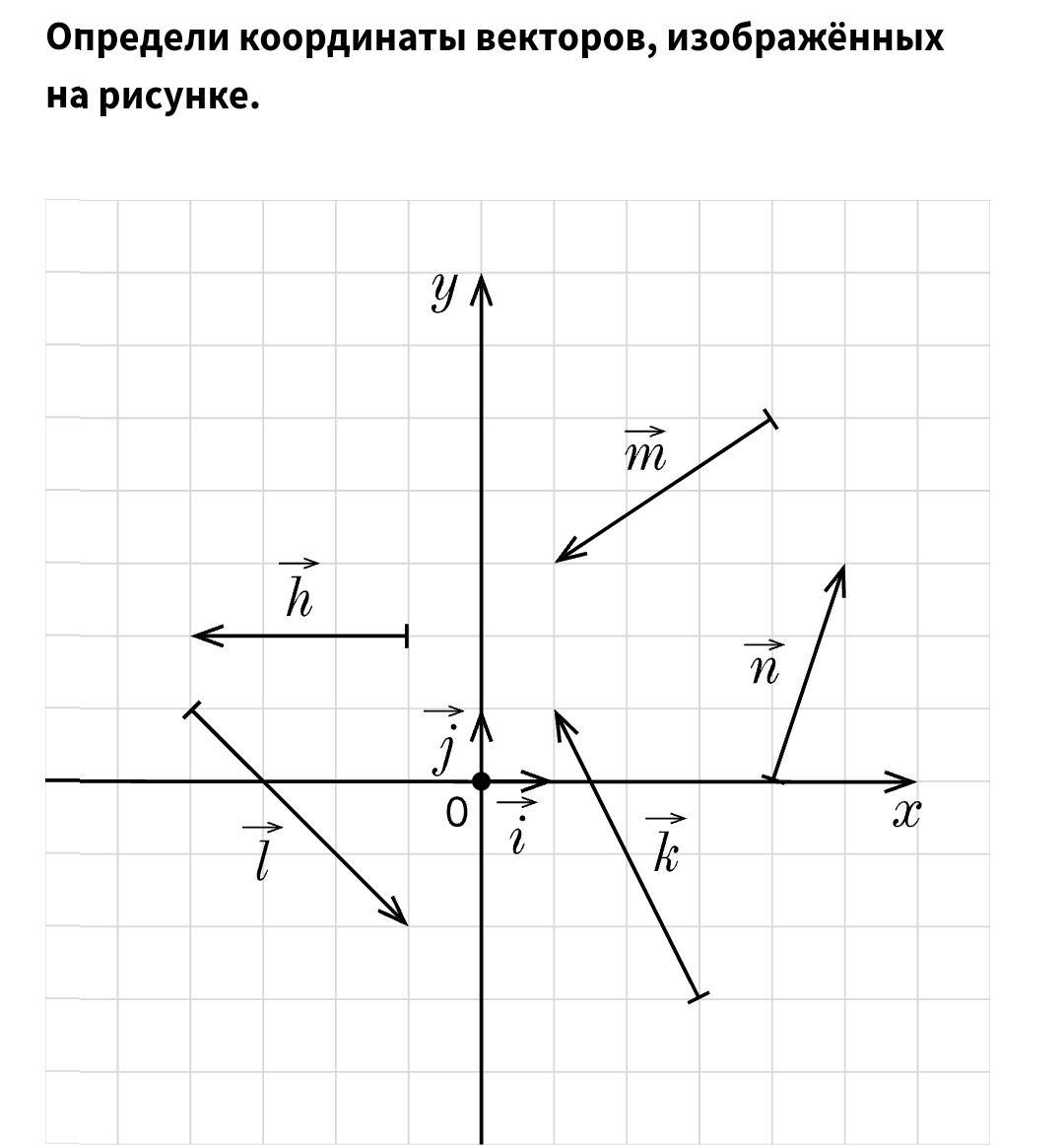

При решении задач на векторы важно учитывать, что правильное понимание координат является основой для вычисления углов, длин и направлений вектора.