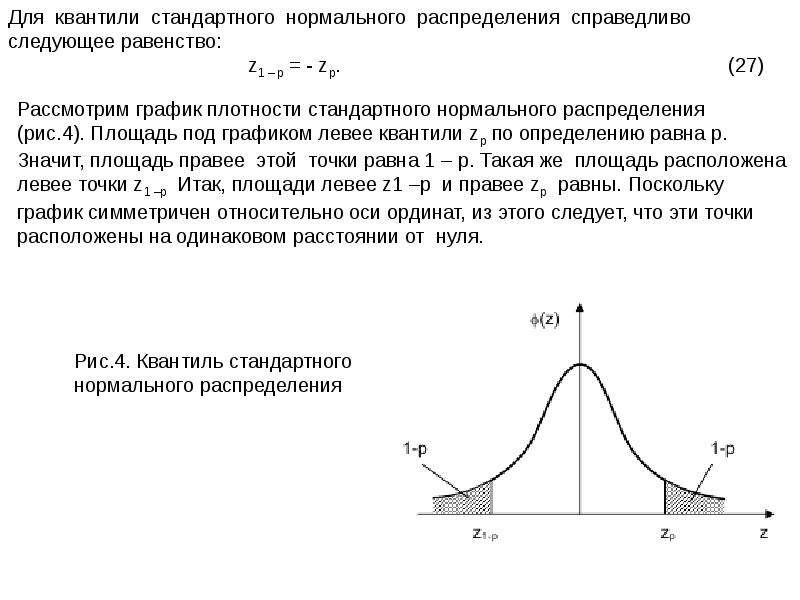
Роль дисперсии в графике нормального распределения и её визуальное отображение
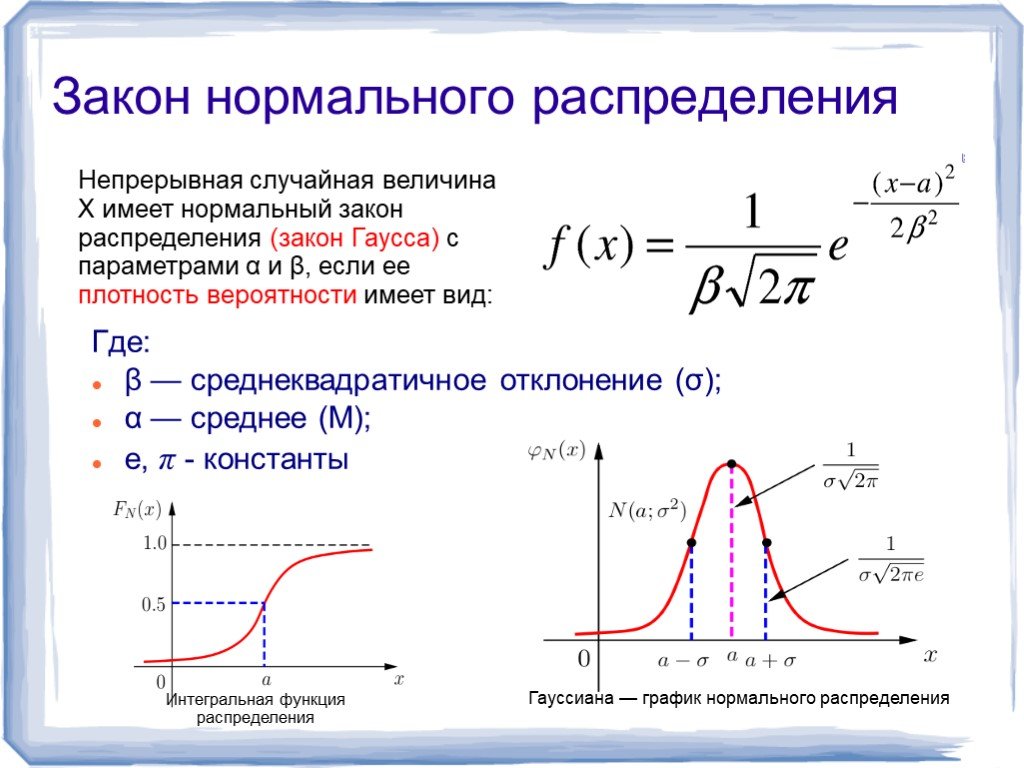
Дисперсия — ключевая характеристика нормального распределения, влияющая на ширину и форму его графика. Этот параметр определяет степень разброса значений вокруг среднего и оказывает существенное влияние на анализ данных и статистические выводы. В этой статье мы собрали полезные советы и информацию о дисперсии и её роли в нормальном распределении.
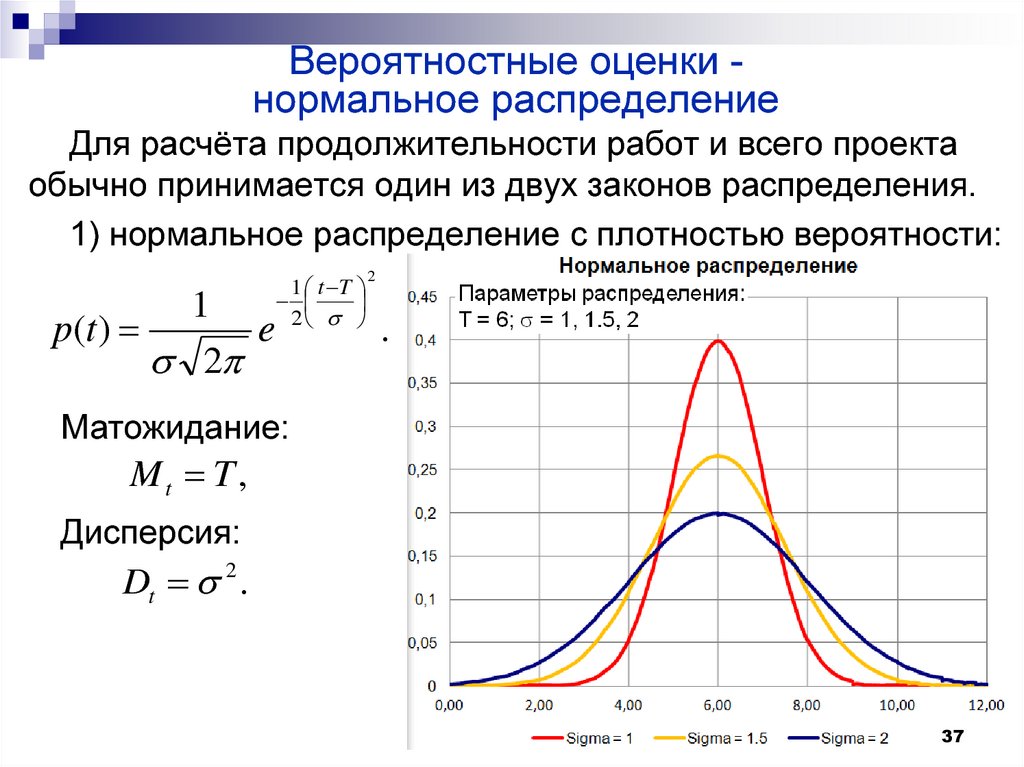

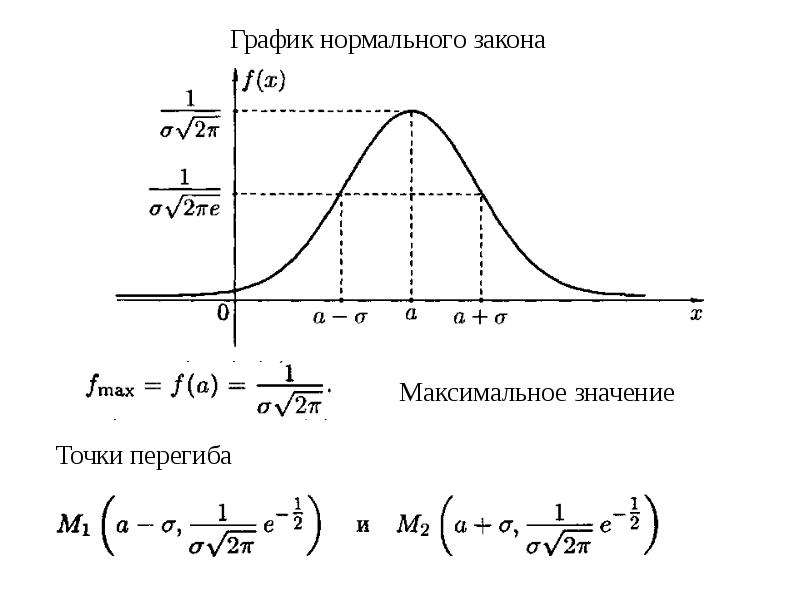
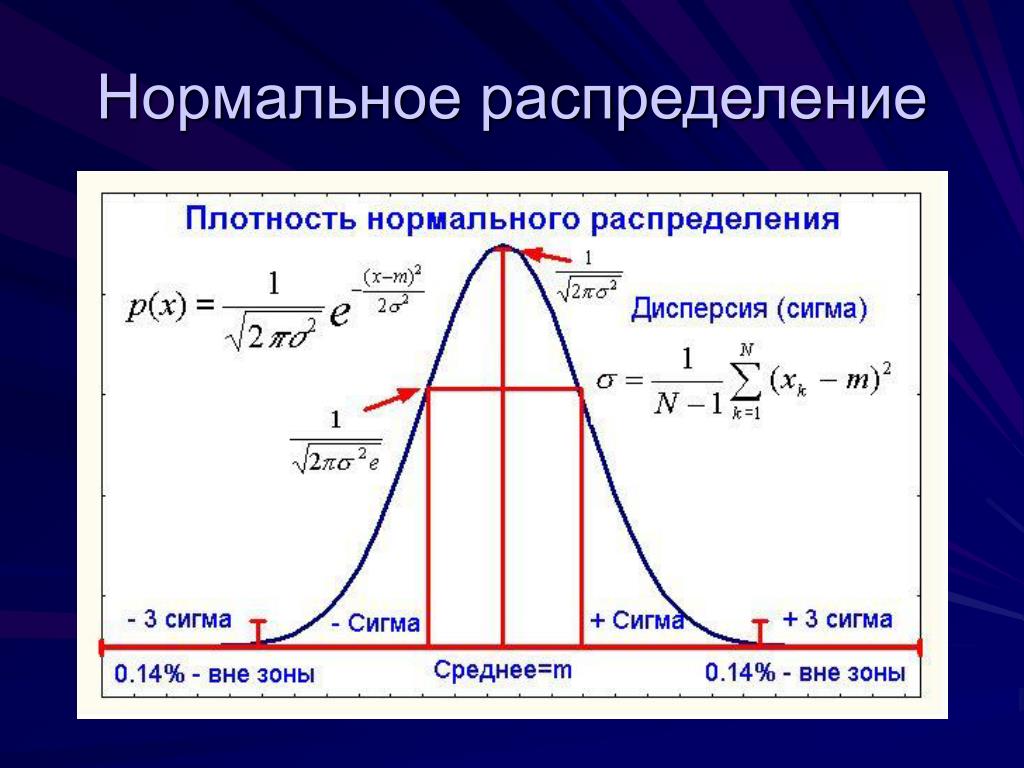
Для визуализации дисперсии на графике нормального распределения обратите внимание на ширину колокола: чем больше дисперсия, тем шире он будет.

Как работать с таблицей стандартного нормального распределения

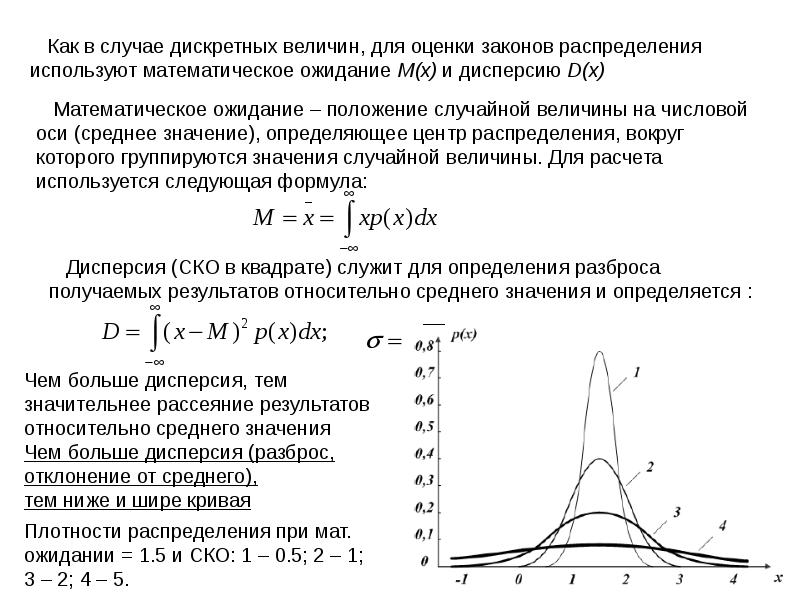
При увеличении дисперсии график нормального распределения становится менее острым и более растянутым, что отражает более значительный разброс данных.
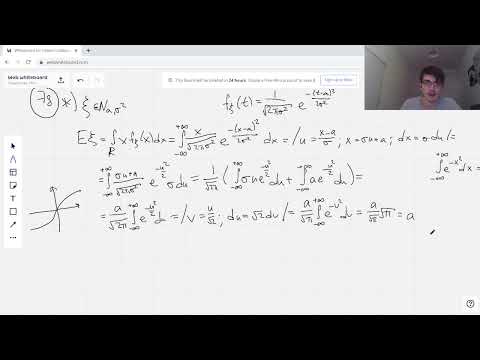
Нормальное распределение: Матожидание и Дисперсия
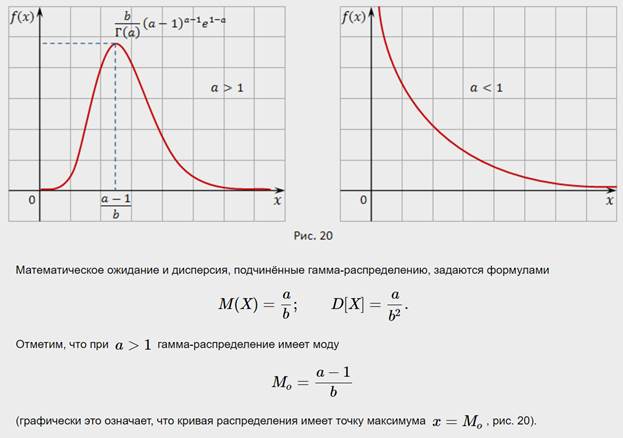
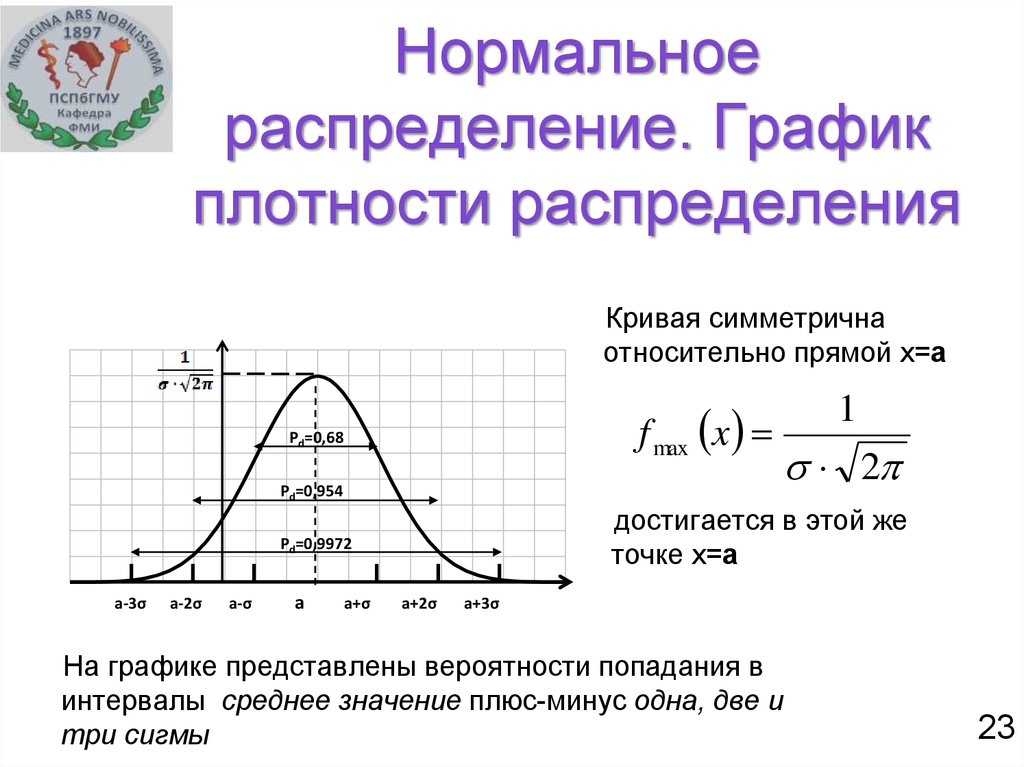
Если дисперсия мала, то значения данных будут сконцентрированы близко к среднему, а график будет узким и высоко расположенным.

Математическое Ожидание, Дисперсия, Стандартное Отклонение за 5 минут
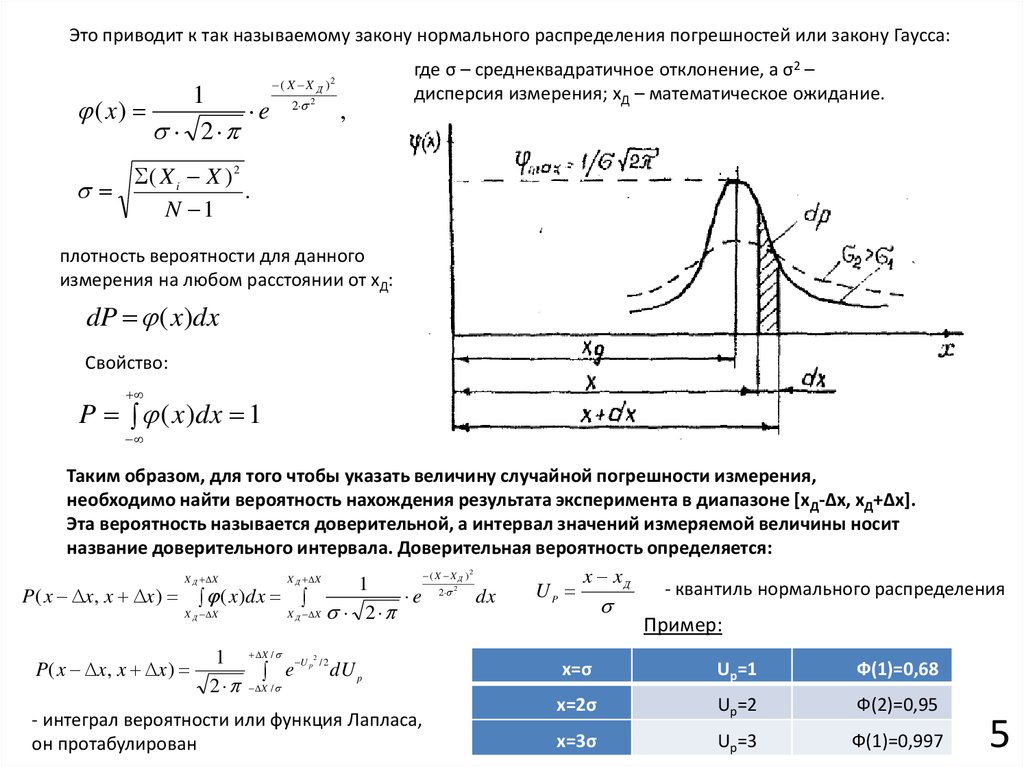
Изменение дисперсии на графике нормального распределения помогает наглядно понять, насколько изменяется вариативность данных при различных сценариях.

Математика без Ху%!ни. Ряд распределения дискретной случайной величины. Мат ожидание и дисперсия.
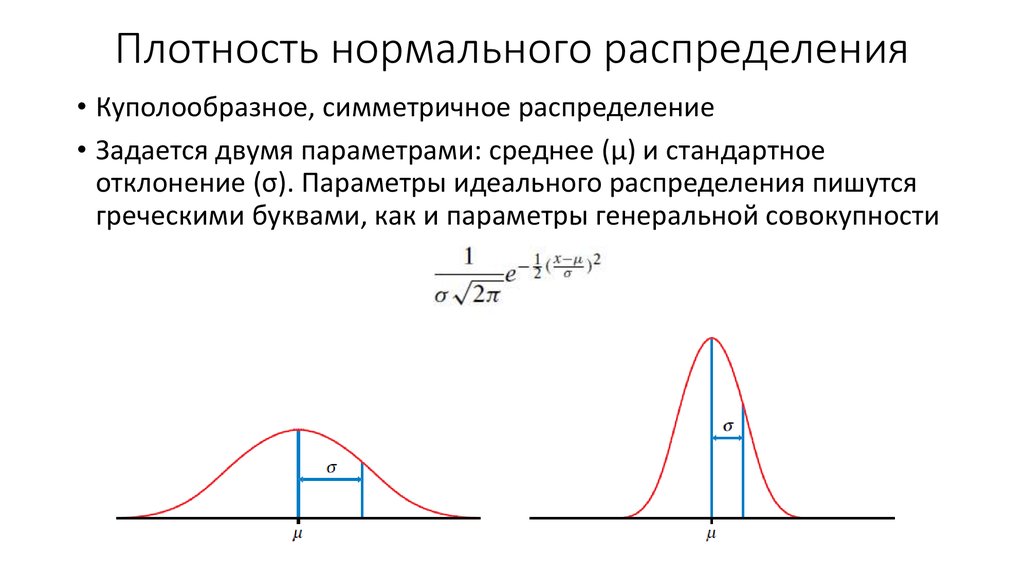
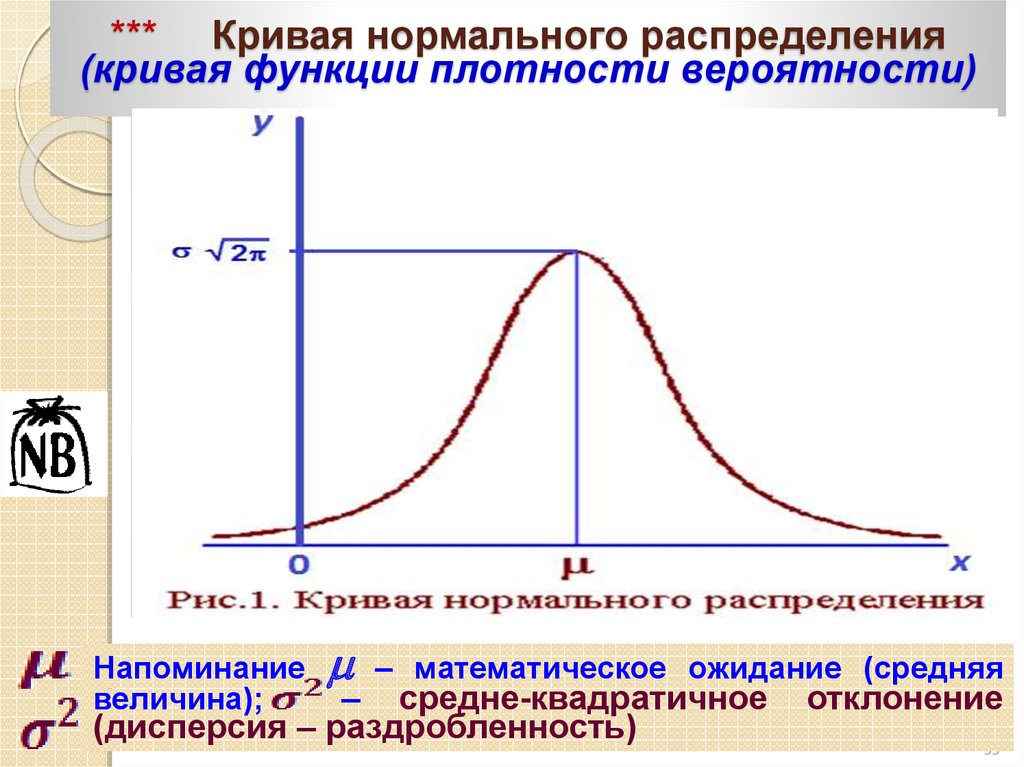
Для практических целей важно учитывать дисперсию, чтобы адекватно интерпретировать данные и избегать ложных выводов, основанных на слишком узких или широких распределениях.
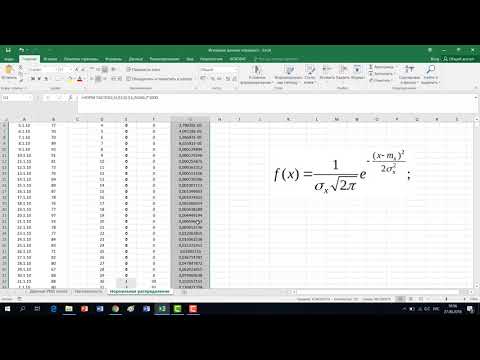
5 Урок Проверка закона нормального распределения
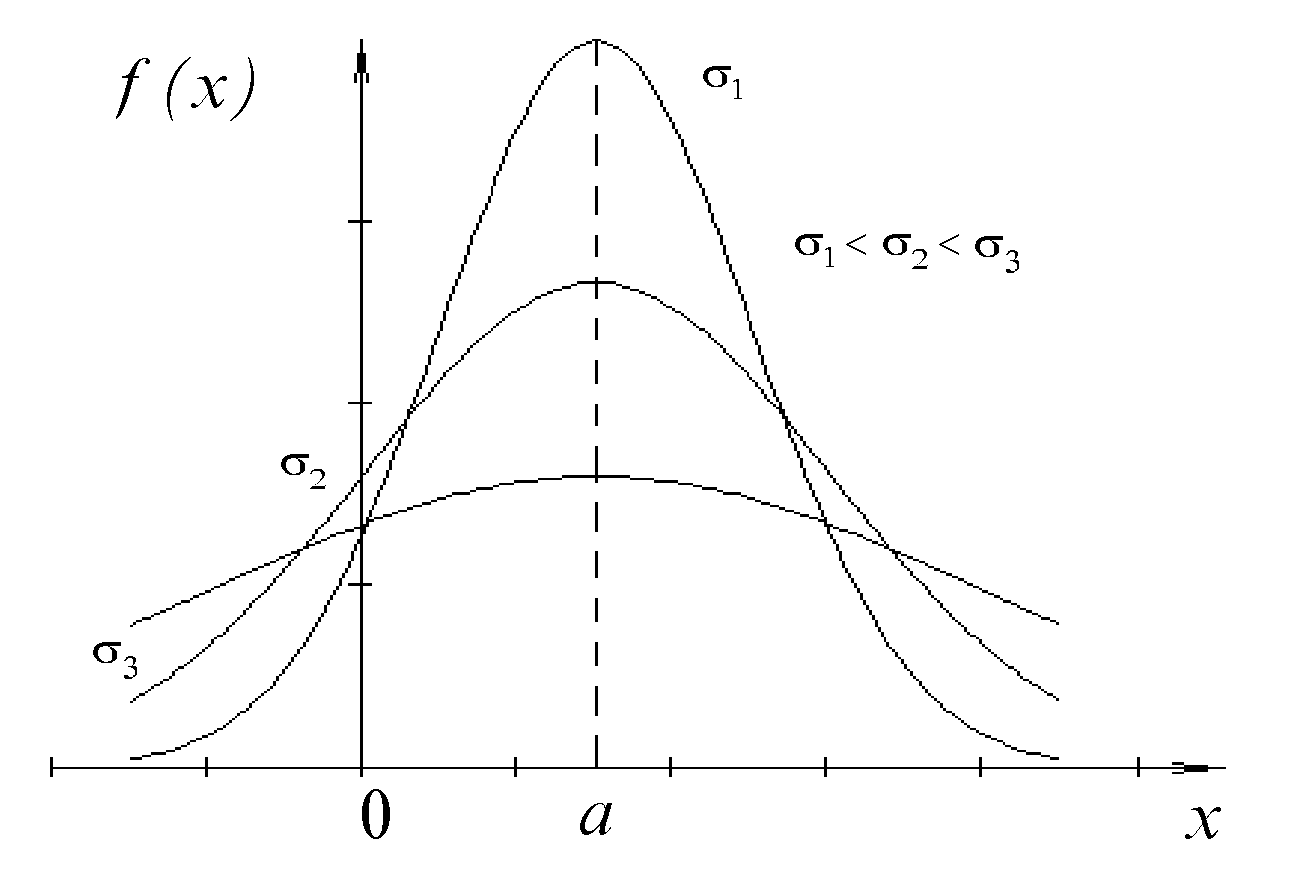
Чтобы оценить степень дисперсии на графике, можно воспользоваться визуальными инструментами, такими как гистограммы или плотности распределения, которые помогают увидеть, как изменяется разброс значений.
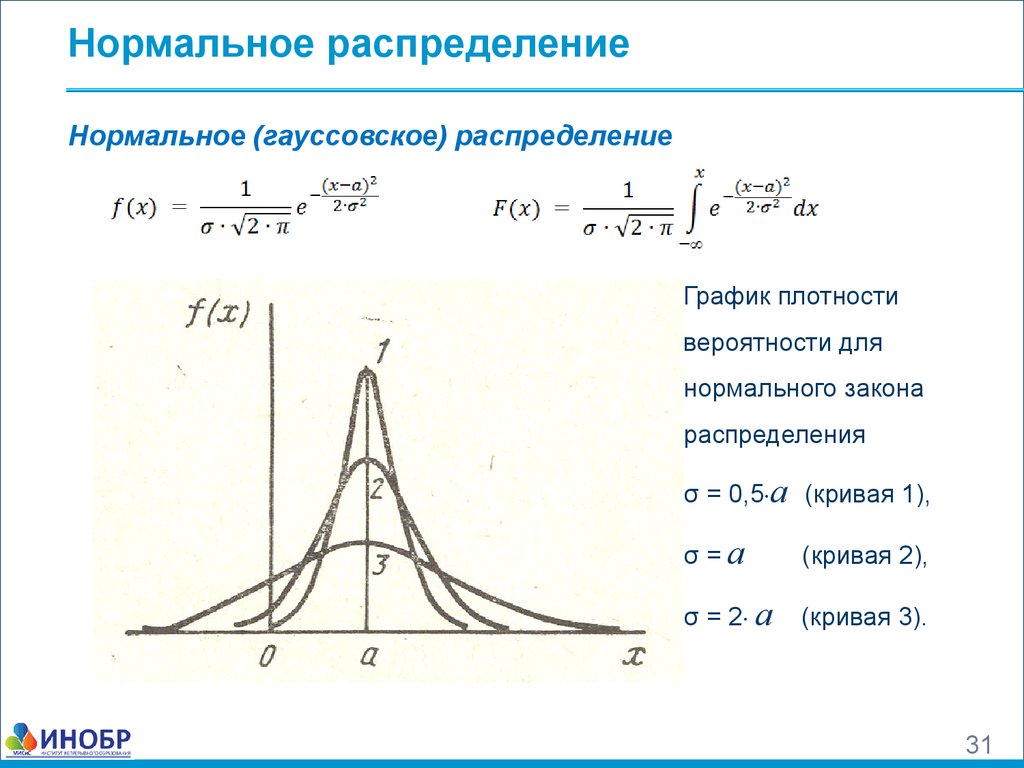
Если дисперсия значительно увеличена, можно ожидать более высокие риски в принятии решений, основанных на таких данных.

Нормальное Распределение за 6 Минут
Использование дисперсии в контексте нормального распределения помогает прогнозировать вариативность будущих данных на основе имеющихся наблюдений.

Самое нормальное распределение // Vital Math

Распределение в Статистике за 5 Минут
При анализе распределений важно учитывать дисперсию, так как она оказывает влияние на точность статистических методов, например, на оценку среднего значения и интервалов доверия.

Старейшая нерешённая задача [Veritasium]

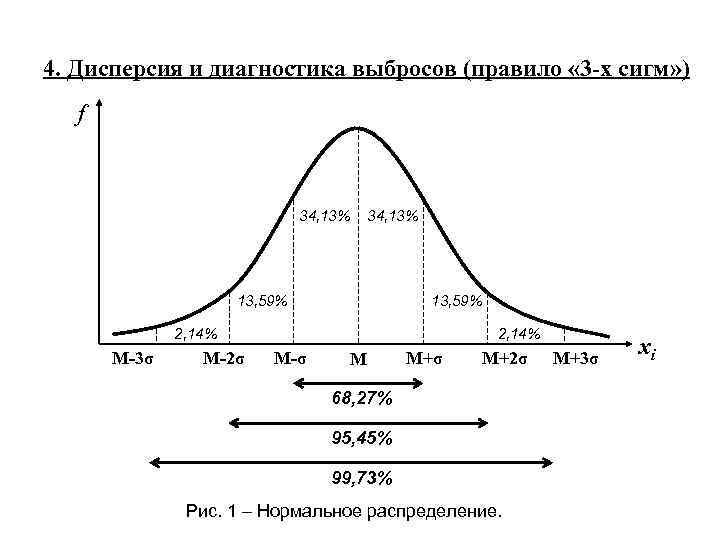
Для лучшего понимания дисперсии и её влияния на распределение полезно использовать интерактивные графики, которые позволяют наглядно менять параметры и наблюдать изменения в реальном времени.