Пошаговое руководство по нахождению расстояния между вершинами в графе: советы и техники
Нахождение расстояния между вершинами графа — важная задача в теории графов, которая находит применение в различных областях, таких как компьютерные сети, навигационные системы и анализ данных. В этой статье собраны основные методы и алгоритмы, которые помогут вам правильно и эффективно решать эту задачу. Здесь вы найдете как теоретические основы, так и практические советы, чтобы успешно определять расстояния между вершинами и оптимизировать выполнение алгоритмов.


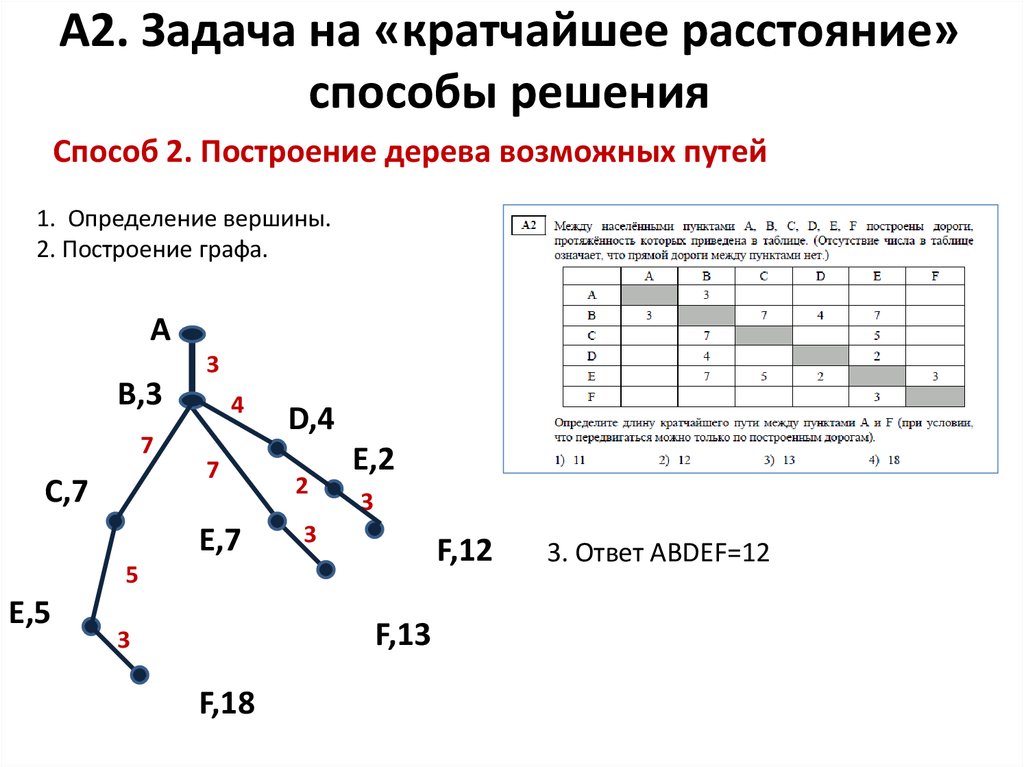
Для поиска кратчайшего пути между двумя вершинами графа используйте алгоритм Дейкстры, если граф взвешенный, и алгоритм BFS для невзвешенных графов.
Нумерация вершин в ориентиованном графе.
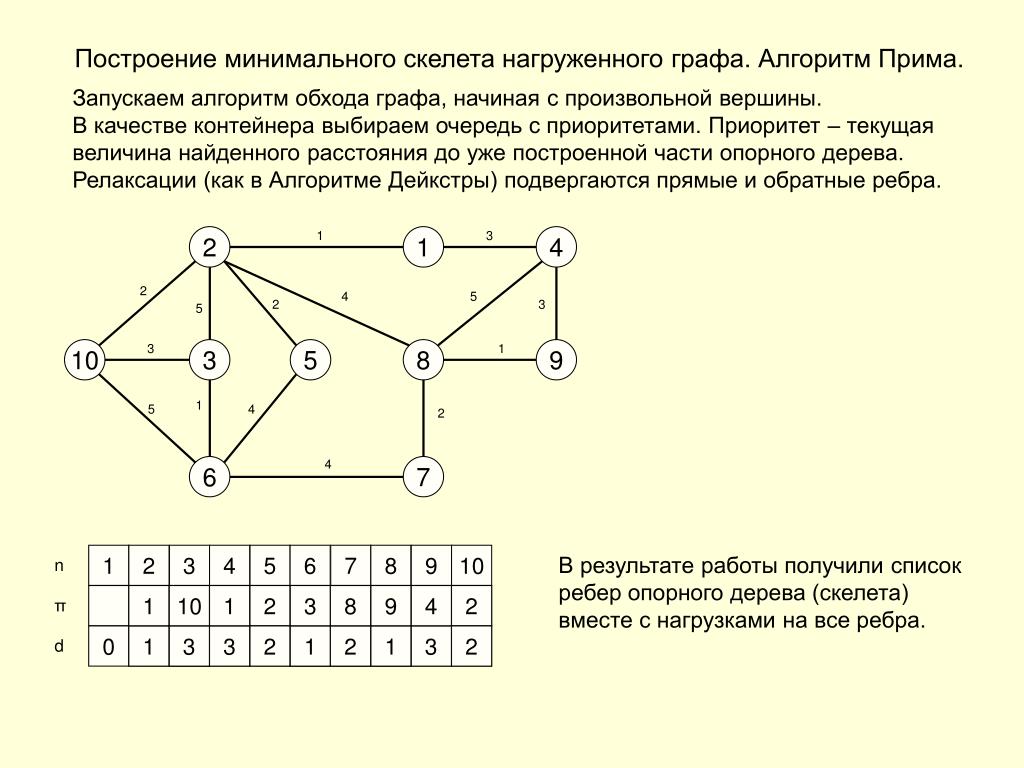
Если граф содержит циклы, учитывайте их при выборе алгоритма, так как это может повлиять на точность результатов.

Моделирование Количество путей через вес вершин графа
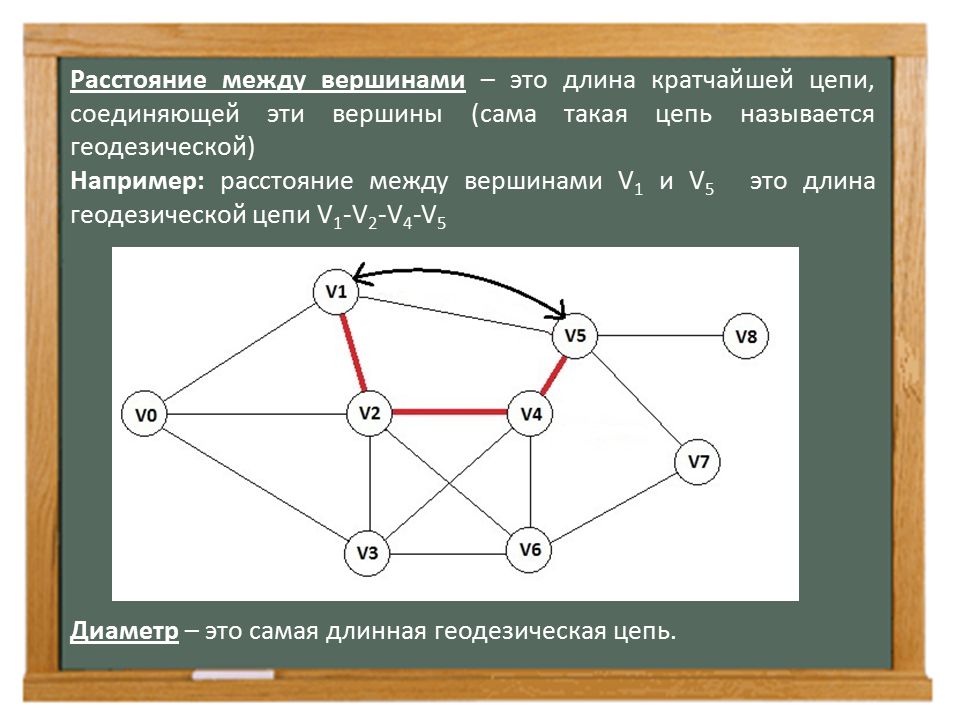
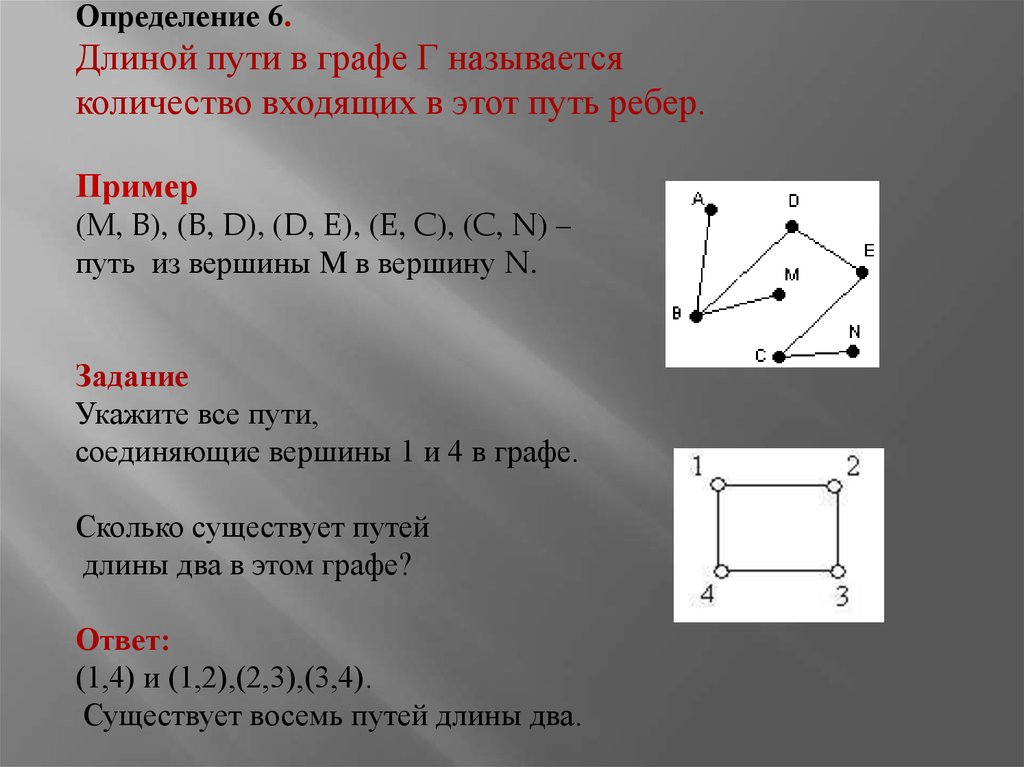
Использование структур данных, таких как кучи и очереди с приоритетом, поможет ускорить выполнение алгоритмов поиска пути.
Поиск расстояния между всеми парами вершин. Алгоритм Уоршалла-Флойда

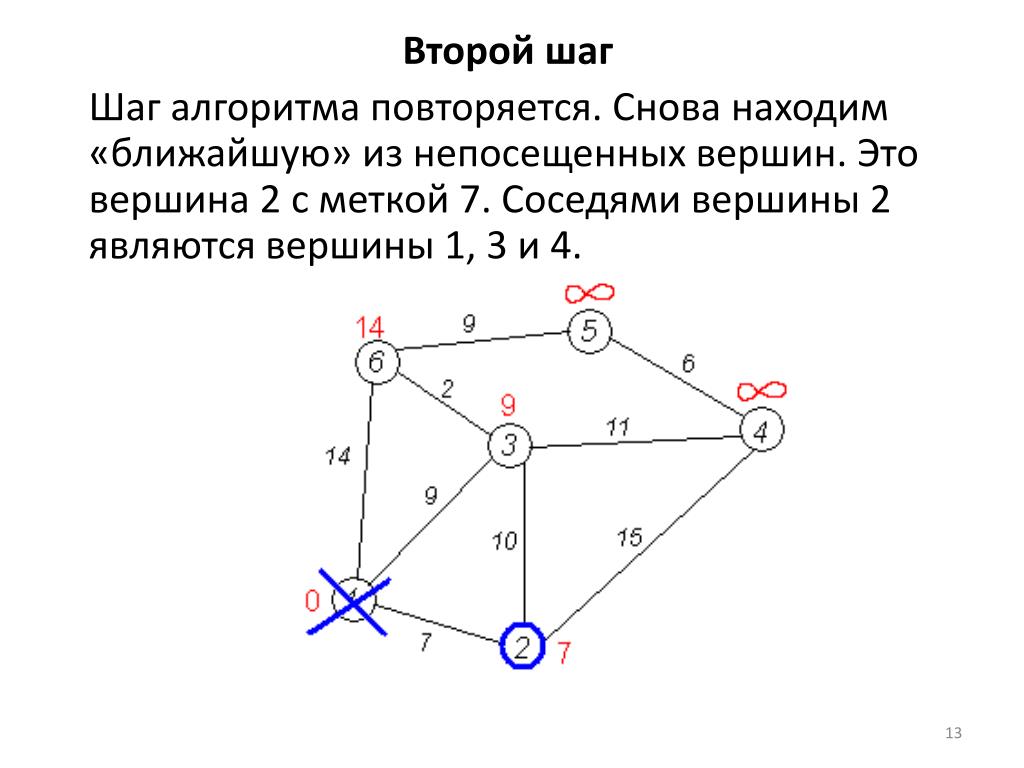
Для больших графов, где нужно найти расстояние между множеством вершин, эффективно использовать алгоритм Флойда-Уоршелла.

Нахождение центра графа
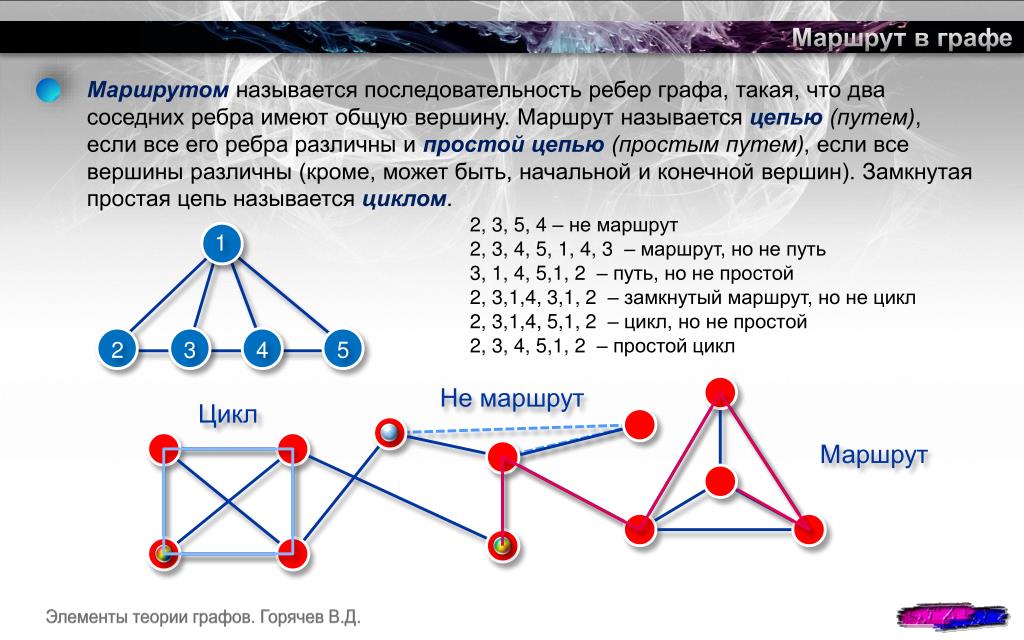
Применение алгоритма A* (A-star) с эвристикой позволяет значительно ускорить нахождение пути в графах с известными ограничениями на пространство поиска.

Операции над графами, маршруты, достижимость, связность, радиостанции
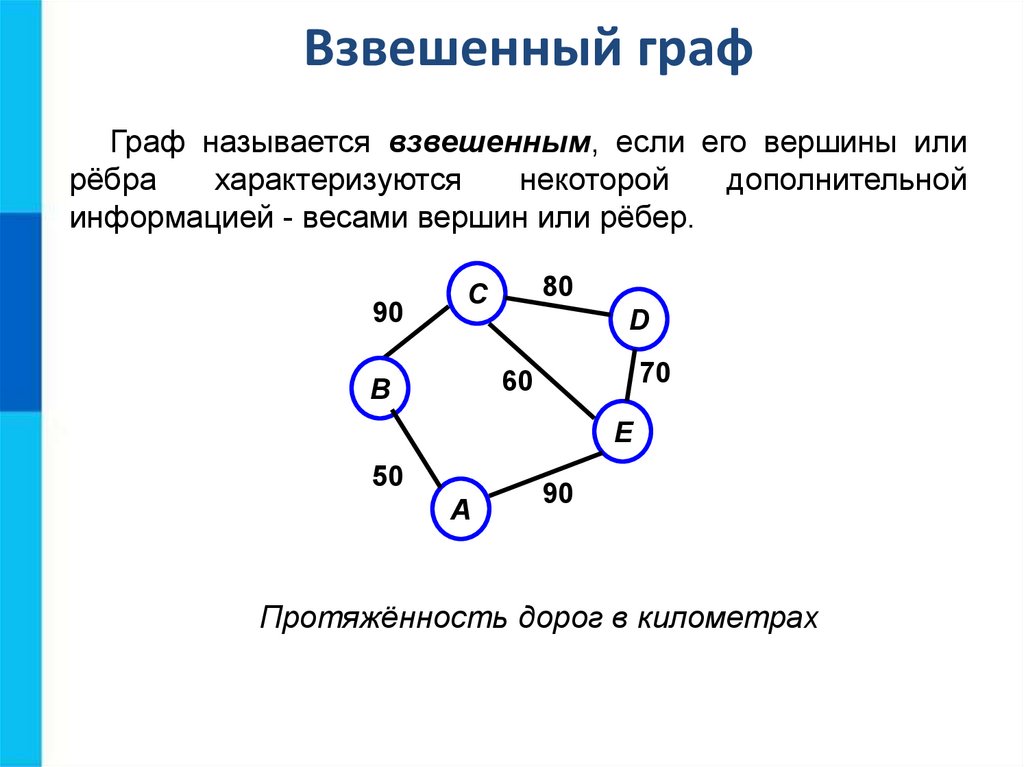
Если нужно найти расстояние между несколькими вершинами сразу, рассмотрите использование алгоритмов, основанных на матрицах смежности, таких как алгоритм Флойда-Уоршелла.
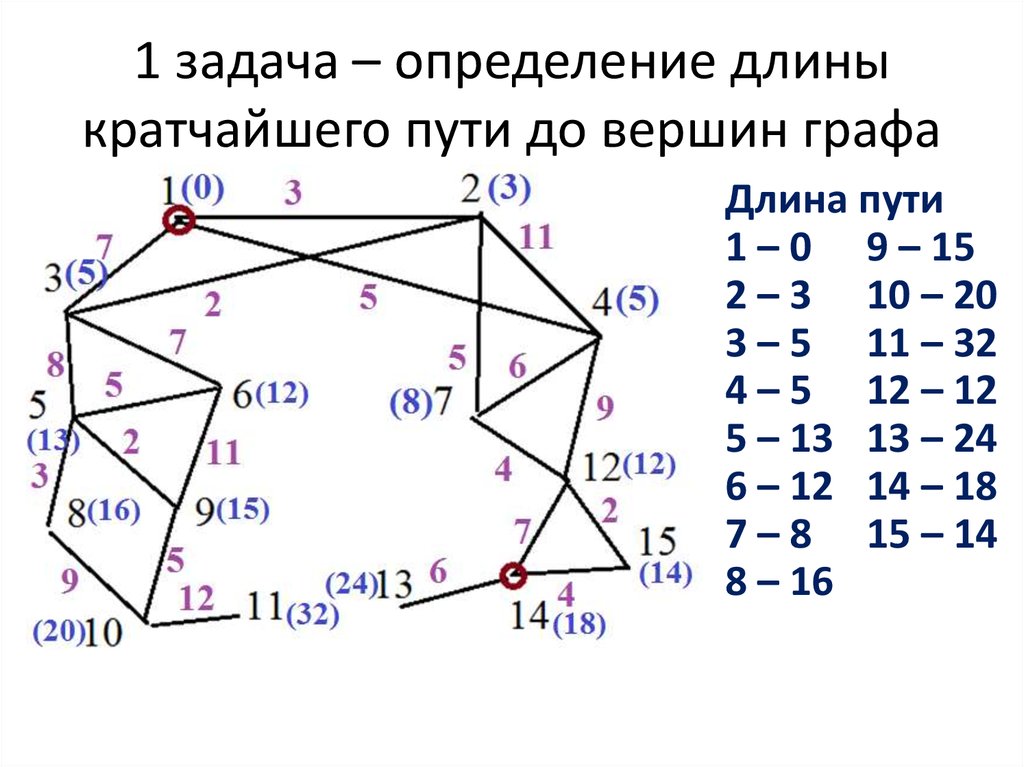
Для графов с динамическими изменениями (например, добавление/удаление рёбер) эффективным решением будет использование алгоритмов, поддерживающих такие изменения, например, динамические алгоритмы поиска путей.
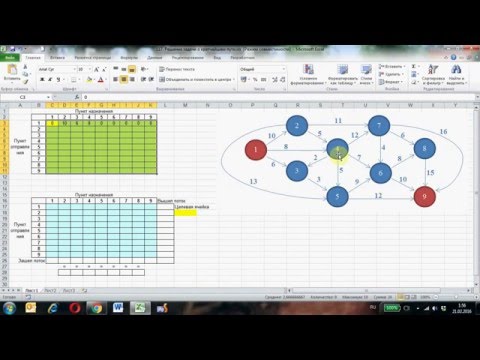
Решение задачи о кратчайшем пути Поиском решений (ориентированный граф)
Не забывайте о том, что в некоторых случаях можно обобщить задачу на многомерные графы, где вычисление расстояний может быть связано с геометрическими расстояниями.
Важным аспектом является правильная нормализация данных, особенно когда графы очень большие и избыточные данные могут замедлить выполнение алгоритмов.
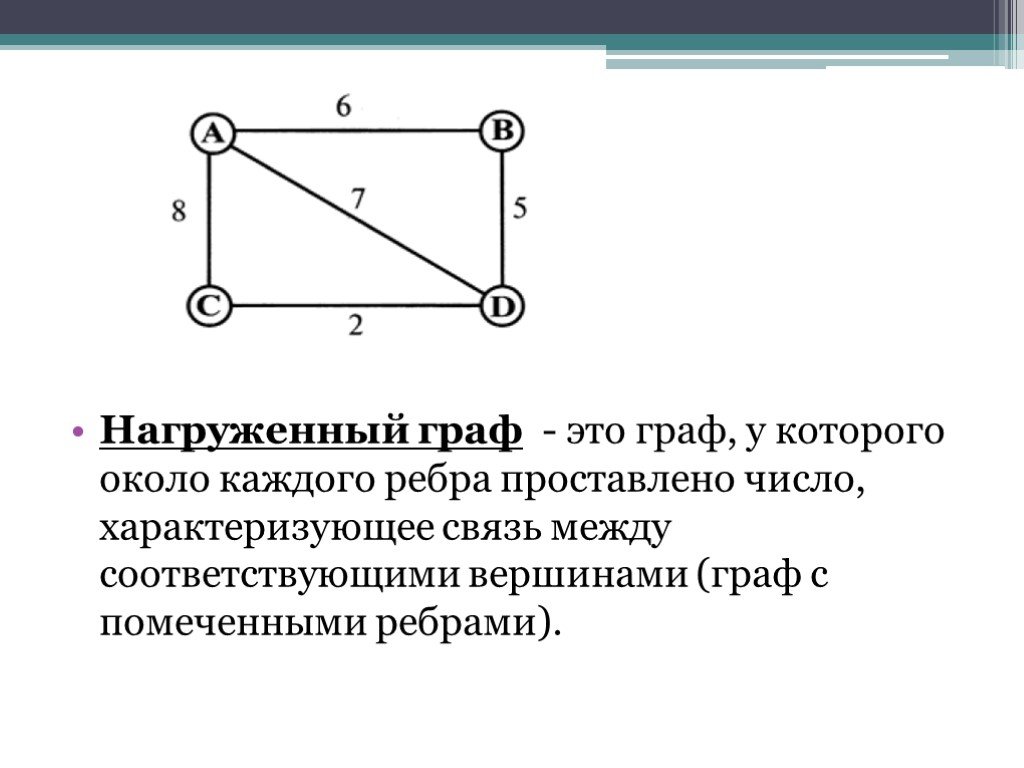
При решении задач на графах всегда полезно проверять граф на наличие отрицательных циклов, чтобы избежать ошибок при применении стандартных алгоритмов поиска кратчайшего пути.

10 Расстояния между вершинами графа
