Как правильно решить задачу с треугольником ABC, учитывая точки Е и К на его сторонах
Задача, связанная с треугольником ABC, в которой точка Е расположена на отрезке AB, а точка К — на отрезке BC, является классическим примером для практики в геометрии. Важно правильно интерпретировать расположение точек на сторонах треугольника и учитывать геометрические свойства таких фигур для нахождения нужных решений. На этой странице мы рассмотрим основные принципы решения таких задач и представим полезные советы для лучшего понимания темы.

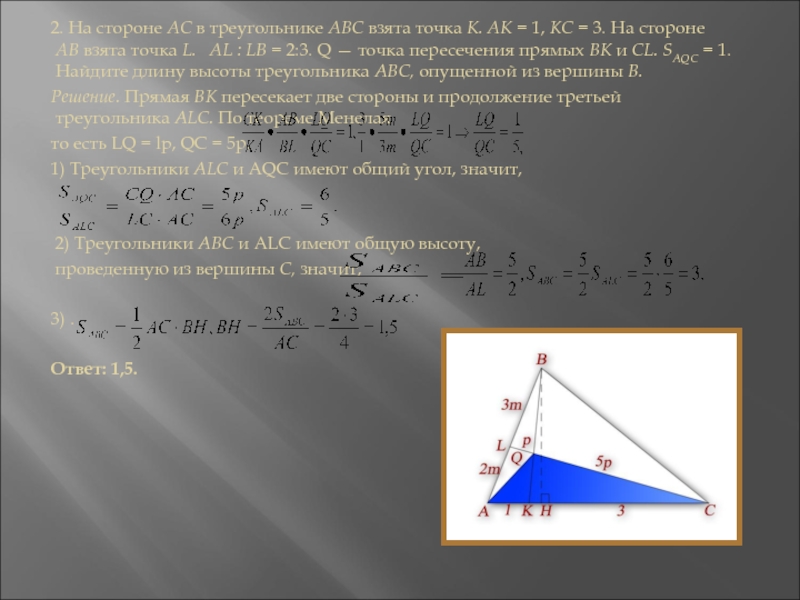
При решении задач с треугольниками важно точно понимать, где расположены точки и какие стороны они пересекают.
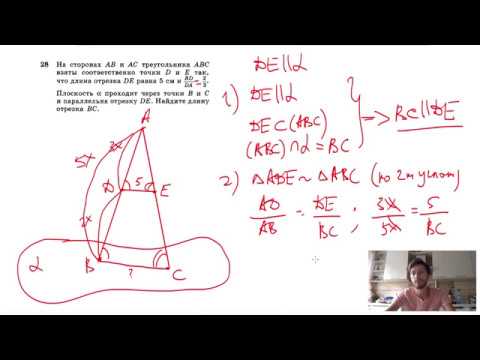
№28. На сторонах АВ и АС треугольника ABC взяты соответственно

Используйте теоремы о подобии треугольников, чтобы упростить вычисления и получить нужные отношения.

Подобие треугольников. Признаки подобия треугольников (часть 1) - Математика

Не забывайте, что если точка лежит на отрезке, это может означать равенство части отрезка и его целого.

Стереометрия 10 класс. Часть 2 - Математика - TutorOnline
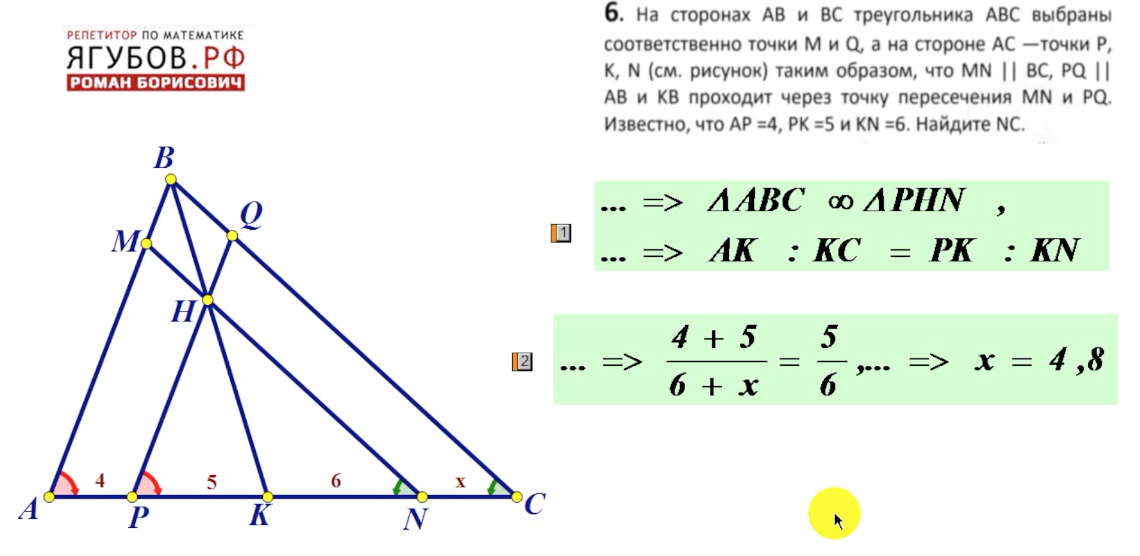
При построении вспомогательных линий в задаче важно использовать прямые и отрезки, которые наглядно иллюстрируют связи между элементами.

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построение
Убедитесь, что правильно используете координаты точек, если задача решается через аналитическую геометрию.

№763. В треугольнике АВС АВ=6, ВС=8, ∠B=90°. Найдите: а) -ВА---ВС- и -ВА- ВС-;

Задачи с пересечением отрезков часто требуют применения теоремы о секущих или аналогичных методов.
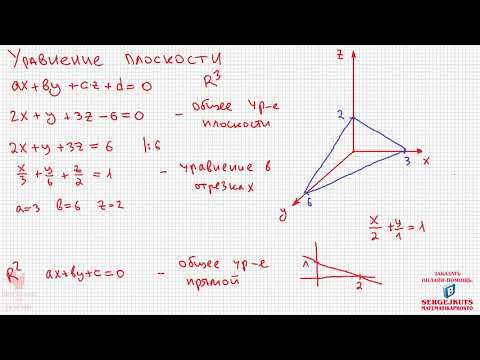
Математика без Ху%!ни. Уравнение плоскости.
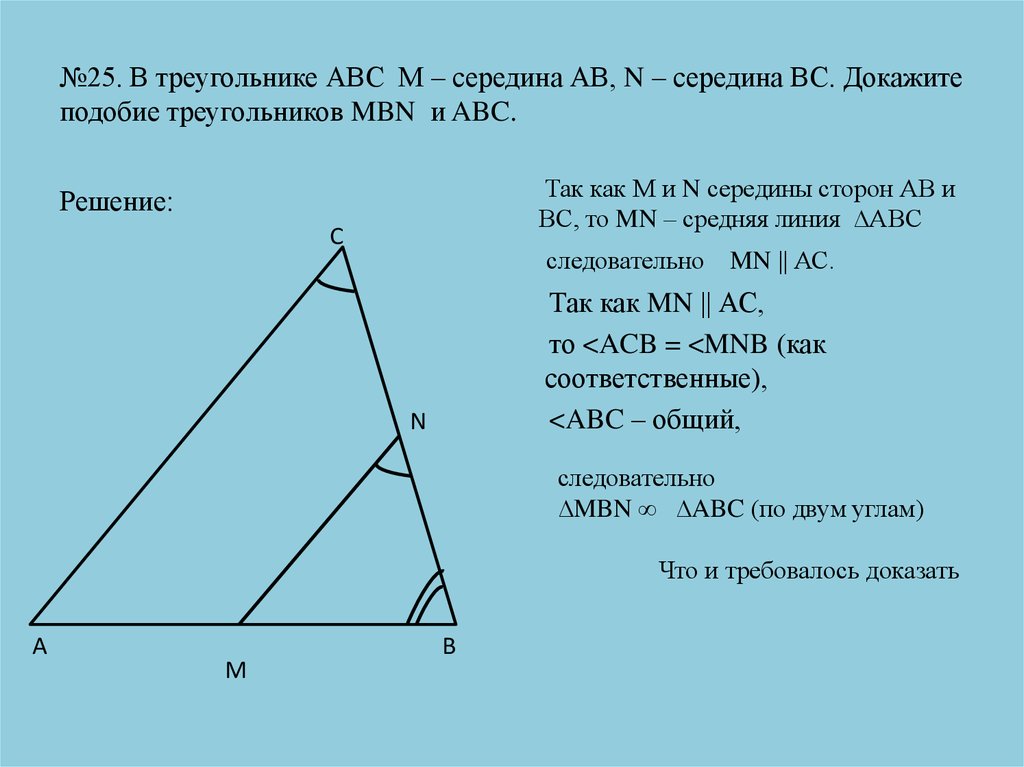
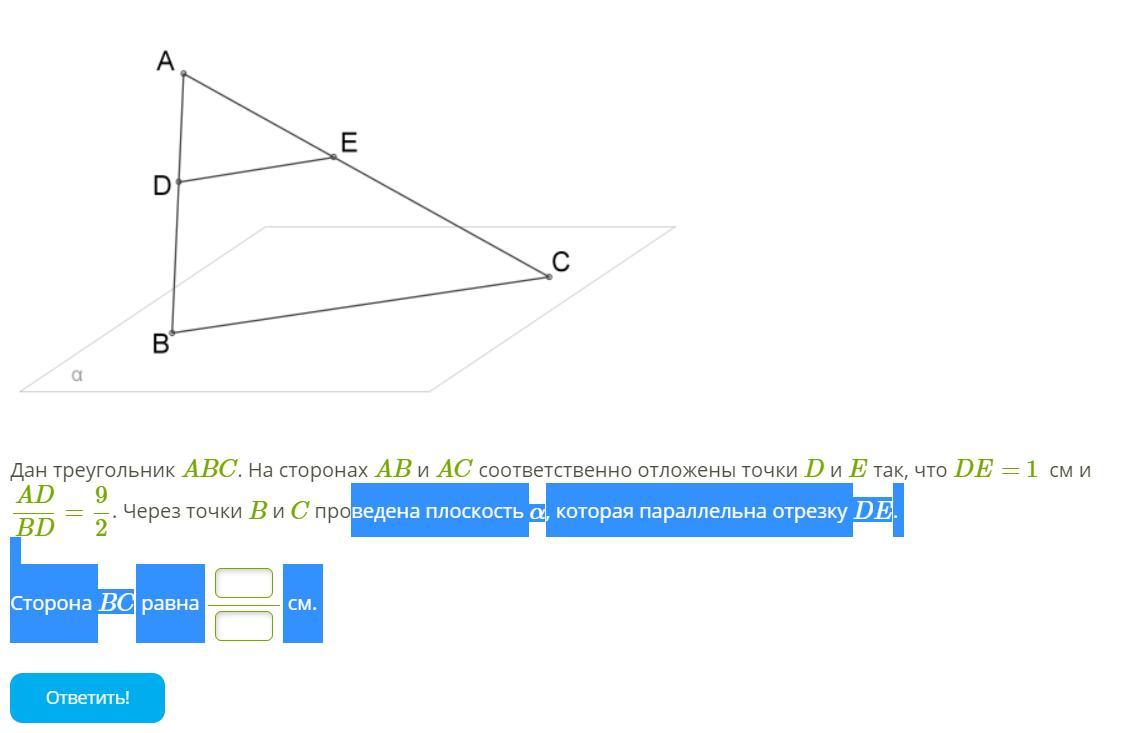
При нахождении отношений длин сторон в треугольнике обращайте внимание на возможные пропорции и применяйте основные теоремы о треугольниках.
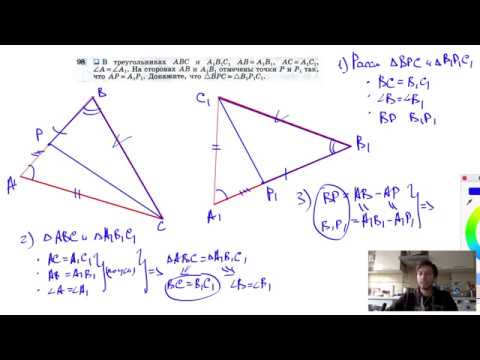
№98. В треугольниках ABC и A1B1C1 AB = А1В1, АС = А1С1, ∠A=∠A1 На сторонах AB и A1B1 отмечены


Для задач с точками на сторонах треугольников часто полезно использовать методы проекций и перпендикуляров.

№764. Пользуясь правилом многоугольника, упростите выражения: а) (АВ + ВС -МС)
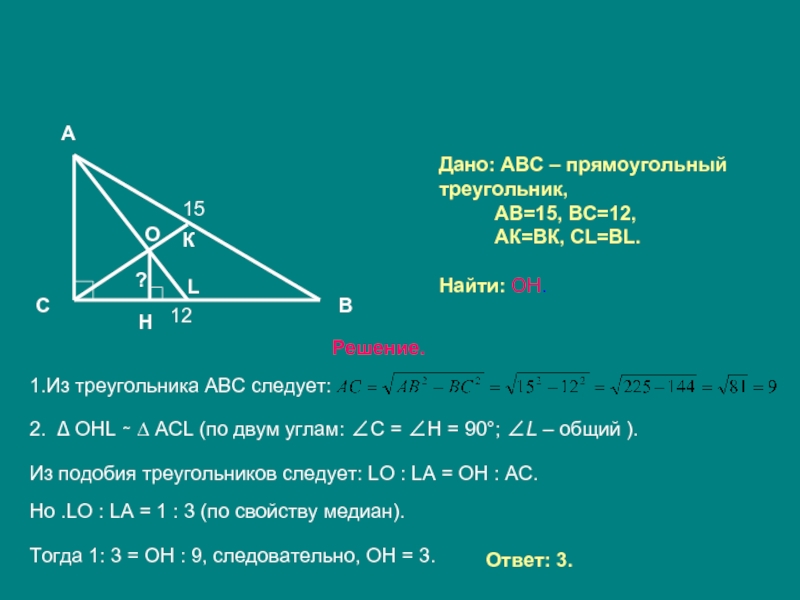

Использование графического метода может помочь лучше визуализировать ситуацию и найти правильное решение.

При решении таких задач не забывайте о симметрии треугольника, она может значительно упростить решение задачи.
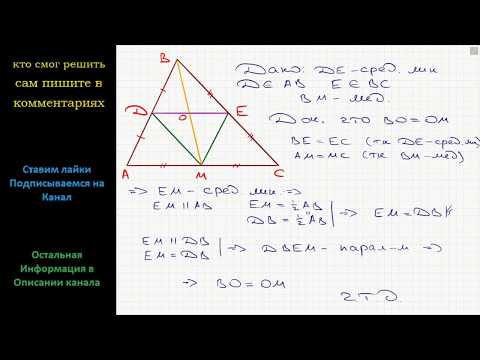
Геометрия Докажите, что средняя линия DE треугольника ABC (точки D и E принадлежат сторонам AB и BC

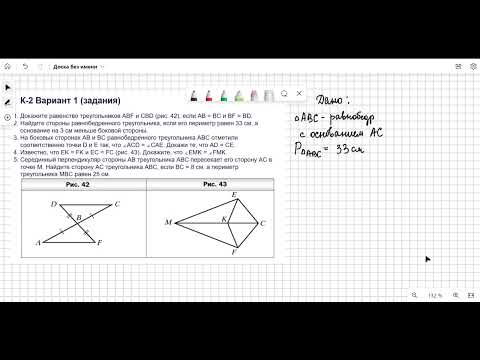
к. р. геометрия Треугольники