Полезные рекомендации по применению метода интегрирования по частям для вычисления интегралов
Метод интегрирования по частям — это важный инструмент в математическом анализе, который позволяет вычислять сложные интегралы, преобразуя их в более простые выражения. В этой статье мы собрали советы и практические рекомендации для успешного применения этого метода, чтобы облегчить вашу работу с определёнными интегралами.


Для начала, убедитесь, что вы правильно выбрали части функции для интегрирования. Обычно одну функцию берут в виде u (которую проще дифференцировать), а другую — в виде dv (которую проще интегрировать).
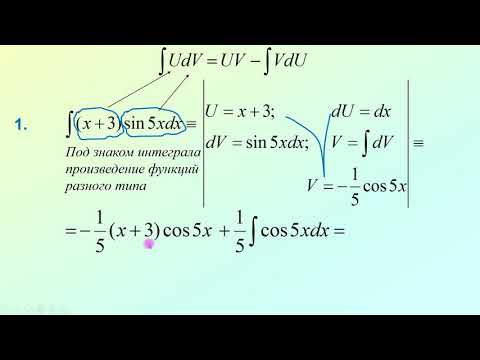
Студентам. Интегрирование по частям

Не забывайте, что правильный выбор функций для разбиения имеет решающее значение. Постарайтесь выбрать такие функции, для которых процесс дифференцирования и интегрирования не станет слишком сложным.

Методы интегрирования. 11 класс.

При решении определённого интеграла учитывайте, что после интегрирования по частям вам может понадобиться выполнить вычисление новых пределов интегрирования для получившихся выражений.

Математика без Ху%!ни. Интегралы, часть 4. Интегрирование по частям.


Если интеграл после первого применения метода не упростился, попробуйте применить метод интегрирования по частям повторно или комбинировать его с другими методами, такими как замена переменной.

Интеграл: Азы интегрирования. Высшая математика
Помните, что интегрирование по частям может быть особенно полезным при решении интегралов с логарифмическими или степенными функциями.

Вычисление определенного интеграла. Практическое занятие. Часть 1

Если вам нужно интегрировать произведение функций, и одна из них является полиномиальной, попробуйте выбрать её для дифференцирования, а другую — для интегрирования.


Когда вы сталкиваетесь с неопределёнными интегралами, всегда учитывайте возможные постоянные интегрирования после каждого шага метода интегрирования по частям.

Неопределённый интеграл. Замена переменной

Если интеграл после применения метода всё ещё остаётся сложным, рассмотрите возможность его вычисления с помощью численных методов или вычислительных программ.

Смысл интеграла и производной. В помощь студенту

Зачем нужен ИНТЕГРАЛ. Объяснение смысла
Внимательно следите за знаком перед результатом в процессе вычислений. Часто при изменении переменных или при дифференцировании возникают знаковые ошибки.

Определенный интеграл по частям Примеры

Регулярно практикуйтесь на различных примерах, чтобы лучше освоить метод интегрирования по частям и научиться быстро находить оптимальные подходы для различных типов интегралов.
