Геометрия равнобедренной трапеции: удивительные свойства пересечения диагоналей
Равнобедренная трапеция с перпендикулярными диагоналями — это интересный и полезный объект в геометрии. Разберем его свойства, применение и решения задач.
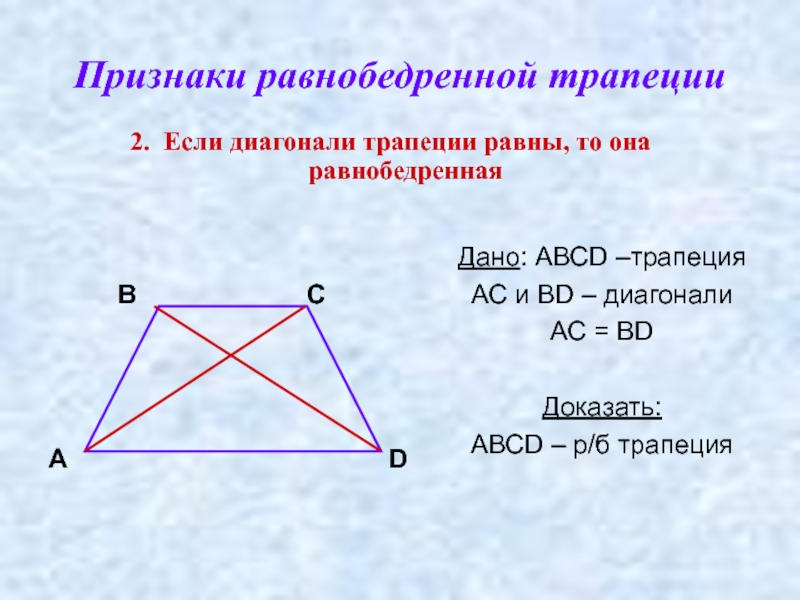

Для равнобедренной трапеции важно помнить, что равенство углов при основаниях помогает доказать перпендикулярность диагоналей.

Геометрия В равнобедренной трапеции одно из оснований равно 40 см, а другое равно 24 см, Диагонали

Проверяйте правильность построения трапеции с помощью дополнительных отрезков и угловых измерений.

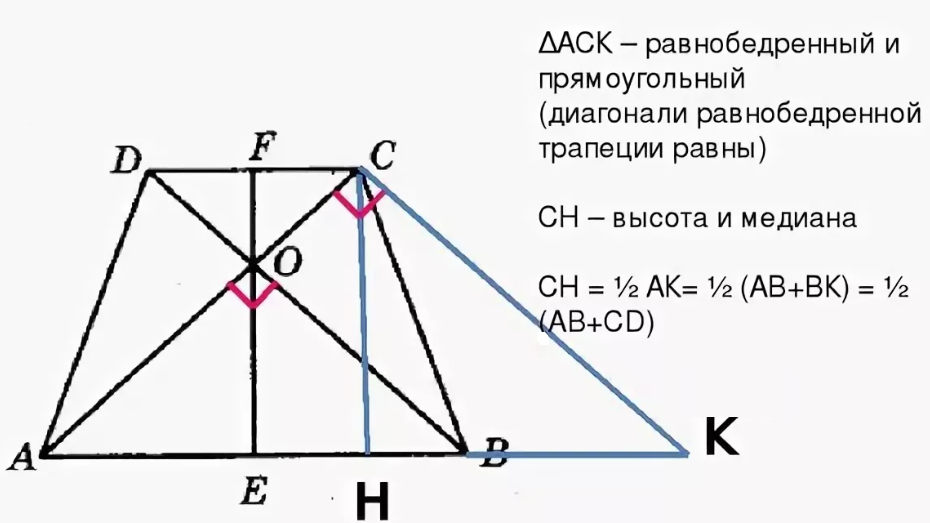
Геометрия Докажите, что если диагонали равнобокой трапеции перпендикулярны, то ее высота равна

Для нахождения длины диагоналей используйте теорему Пифагора в подходящих треугольниках.
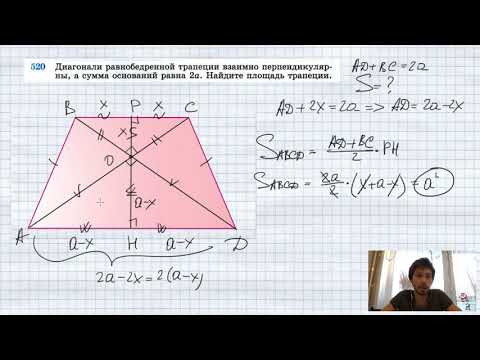
№520. Диагонали равнобедренной трапеции взаимно перпендикулярны, а сумма ее оснований равна 2а
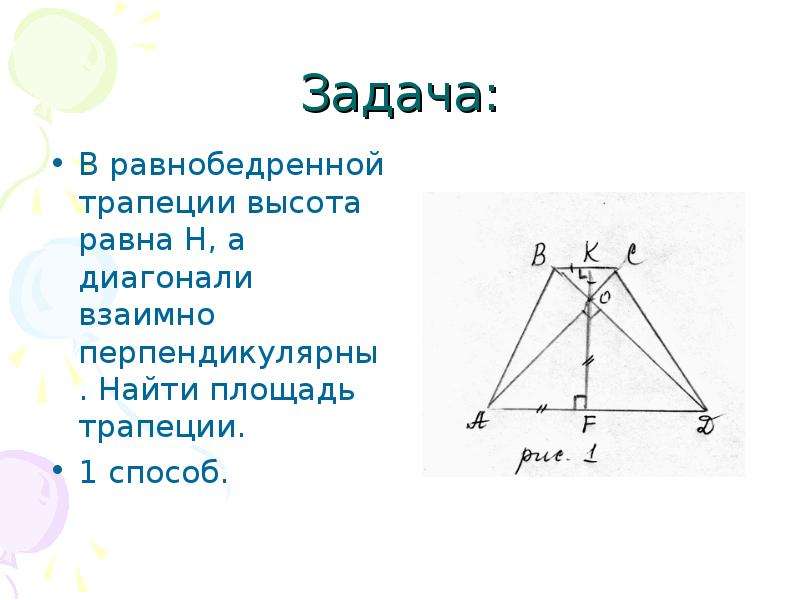
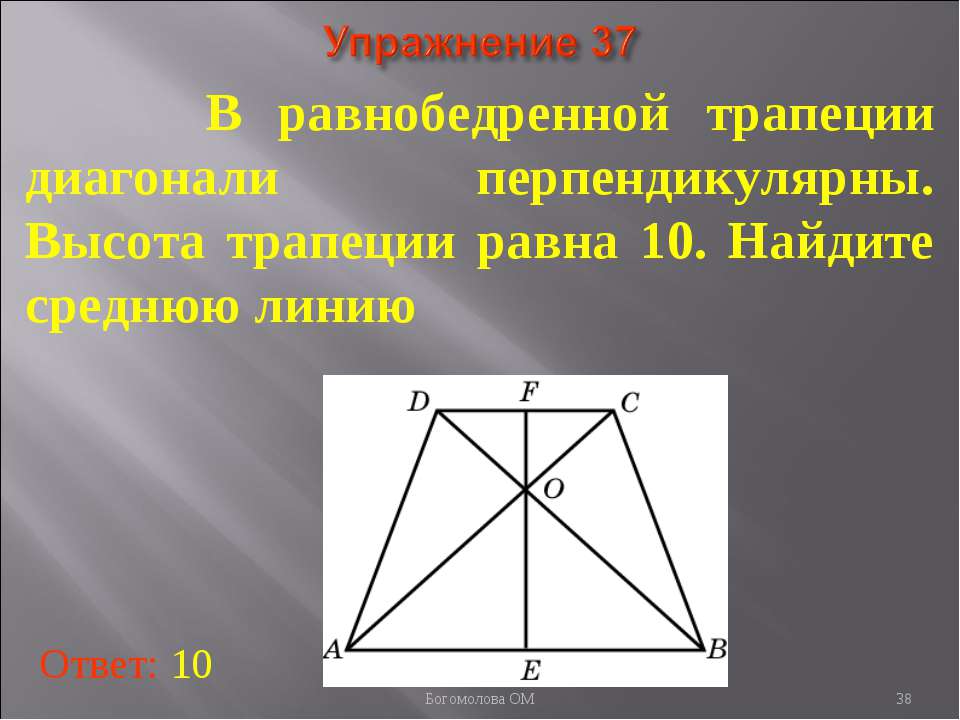
Убедитесь, что трапеция действительно равнобедренная: основания параллельны, а боковые стороны равны.

«Когда мозги не заложишь!»: Наталья Касперская об экономических реалиях российской IT-отрасли
Перпендикулярность диагоналей можно подтвердить через скалярное произведение их направляющих векторов.
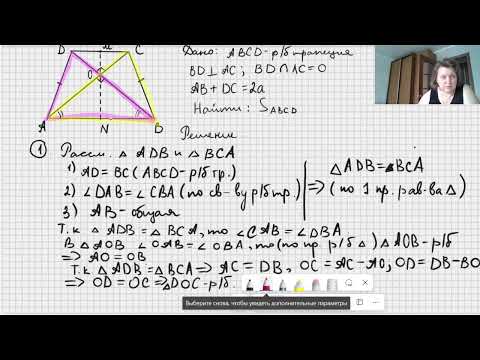
Равнобедренная трапеция.
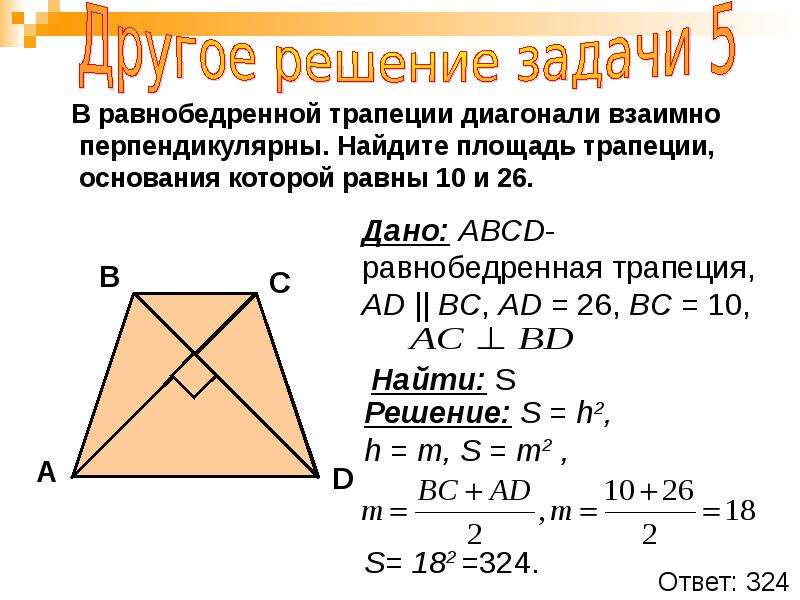

Используйте центр трапеции как точку пересечения диагоналей для проверки симметрии фигуры.
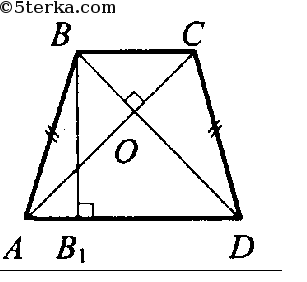
Рассчитайте площади треугольников, на которые диагонали делят трапецию, для проверки равенства.

Всё о трапеции за 60 секунд
Обратите внимание на пропорции между основаниями и высотой трапеции — это ключ к правильному решению задач.
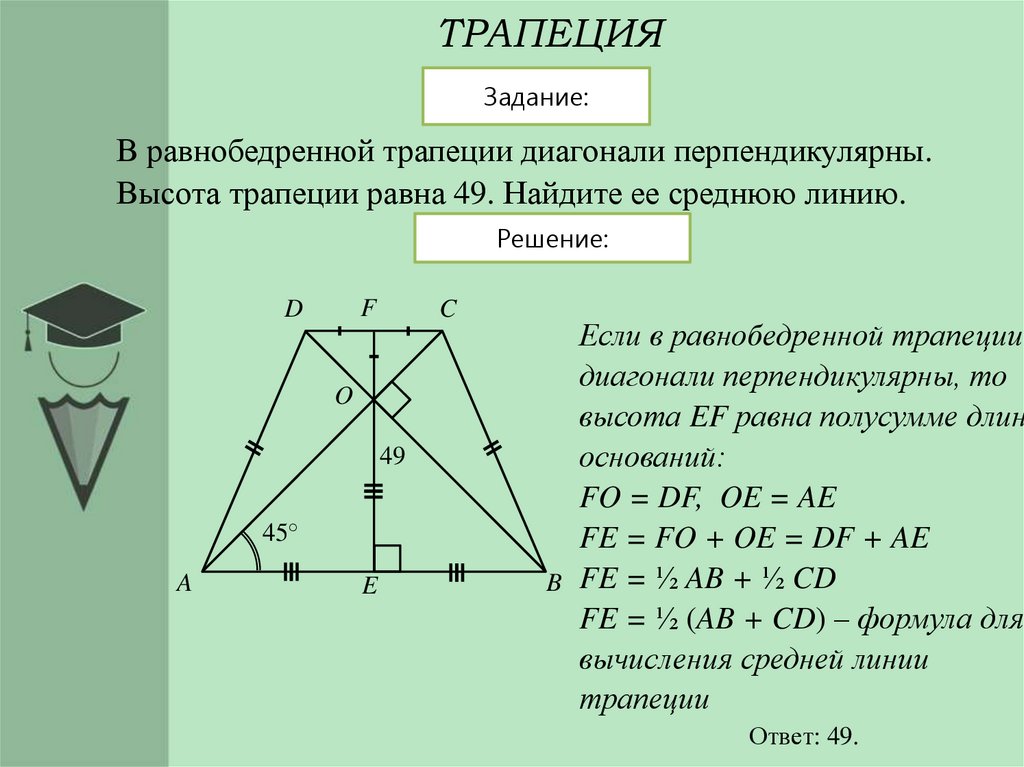
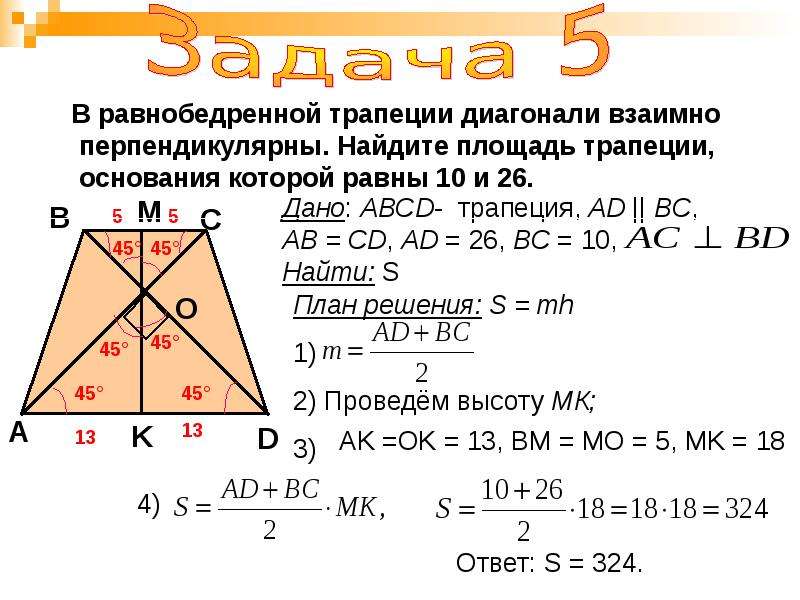
Помните, что равнобедренная трапеция всегда вписывается в окружность, если диагонали взаимно перпендикулярны.

Для упрощения расчетов используйте координатный метод: задайте вершины трапеции на плоскости.

Геометрия Диагонали трапеции перпендикулярны одна из них равна 48 см а средняя линия трапеции 25 см

Задача из вступительных в Гарвард. 99% не смогли решить