Как правильно построить гиперболу второго порядка: важные рекомендации и наглядные примеры
Этот материал поможет вам разобраться с процессом построения гиперболы второго порядка, шаг за шагом объясняя основные этапы. Вы узнаете, как правильно выделить основные характеристики гиперболы, а также получите полезные советы для быстрого и точного выполнения задачи.
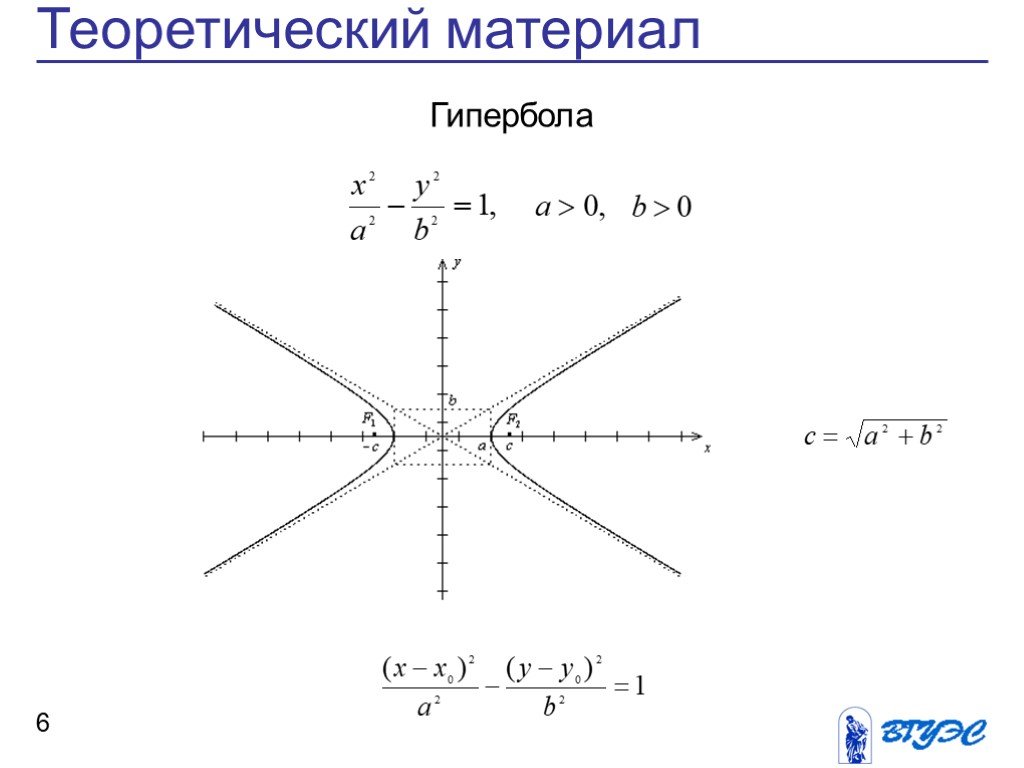

Для начала обязательно найдите фокусы гиперболы и определите ее асимптоты — это ключевые элементы при построении.

Кривые второго порядка


Не забывайте, что у гиперболы есть две ветви, каждая из которых имеет свою асимптоту. Отражение этой особенности важно при построении.

Приведение гиперболы к каноническому виду: поворот, построение
Для удобства используйте графики на бумаге с заранее нанесенной сеткой, это поможет точно отложить все ключевые точки.
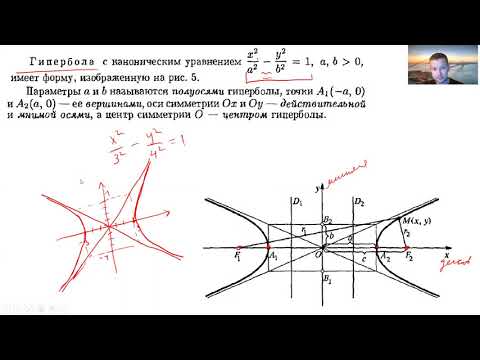
Кривые второго порядка. Гипербола

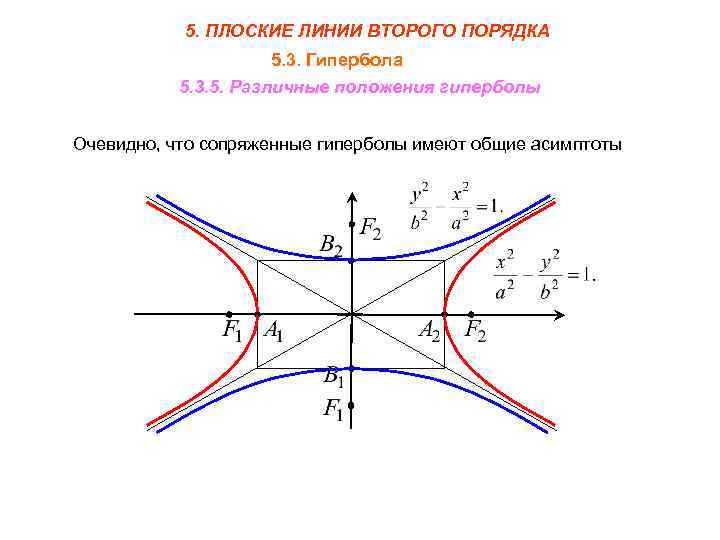
Запомните, что стандартное уравнение гиперболы второго порядка может выглядеть как (x²/a²) - (y²/b²) = 1 или (y²/b²) - (x²/a²) = 1, в зависимости от ориентации осей.

Лекция 31.2. Кривые второго порядка. Гипербола.
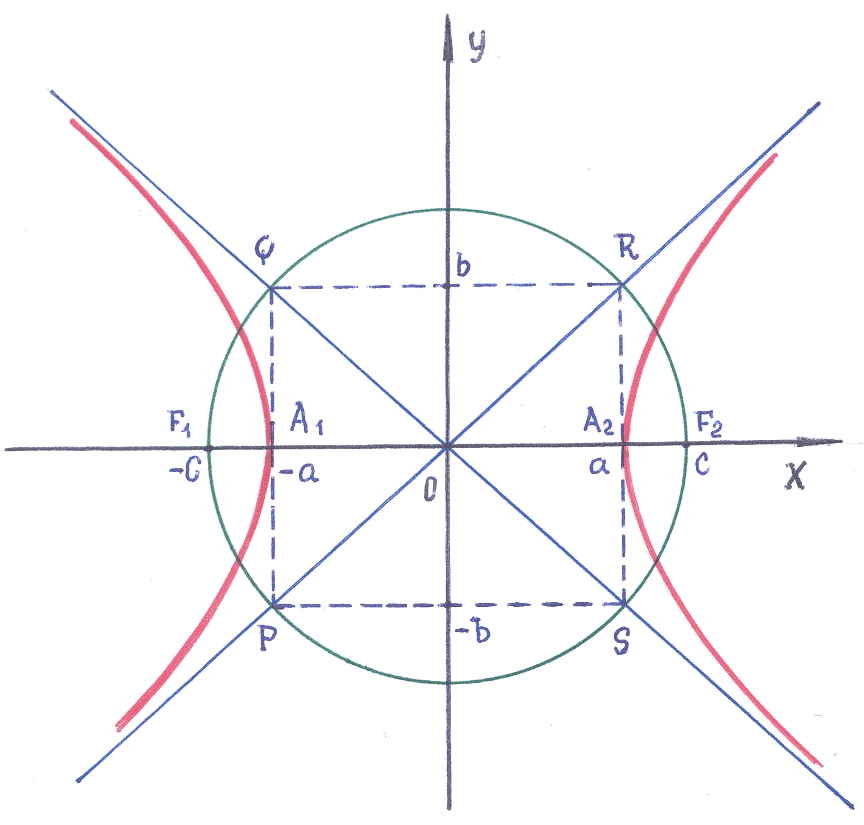

Следите за точностью при нахождении фокусов — ошибка на этом этапе повлияет на точность всего построения.
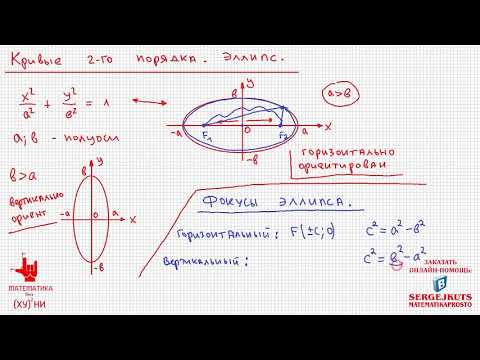
Математика без Ху%!ни. Кривые второго порядка. Эллипс.
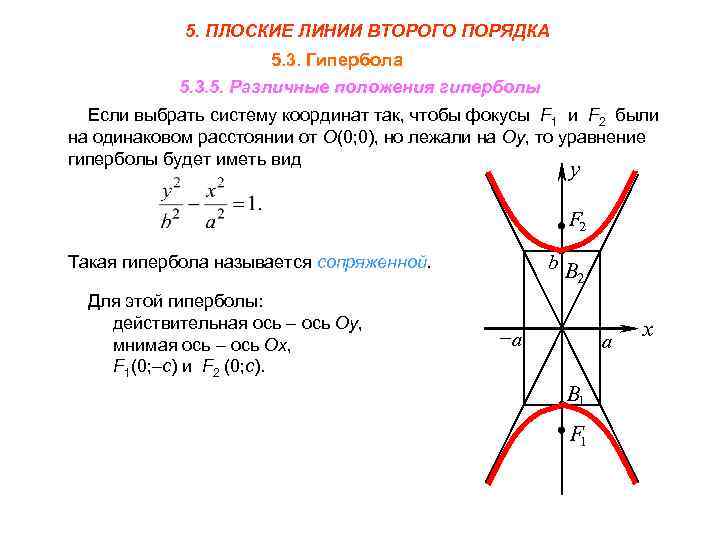
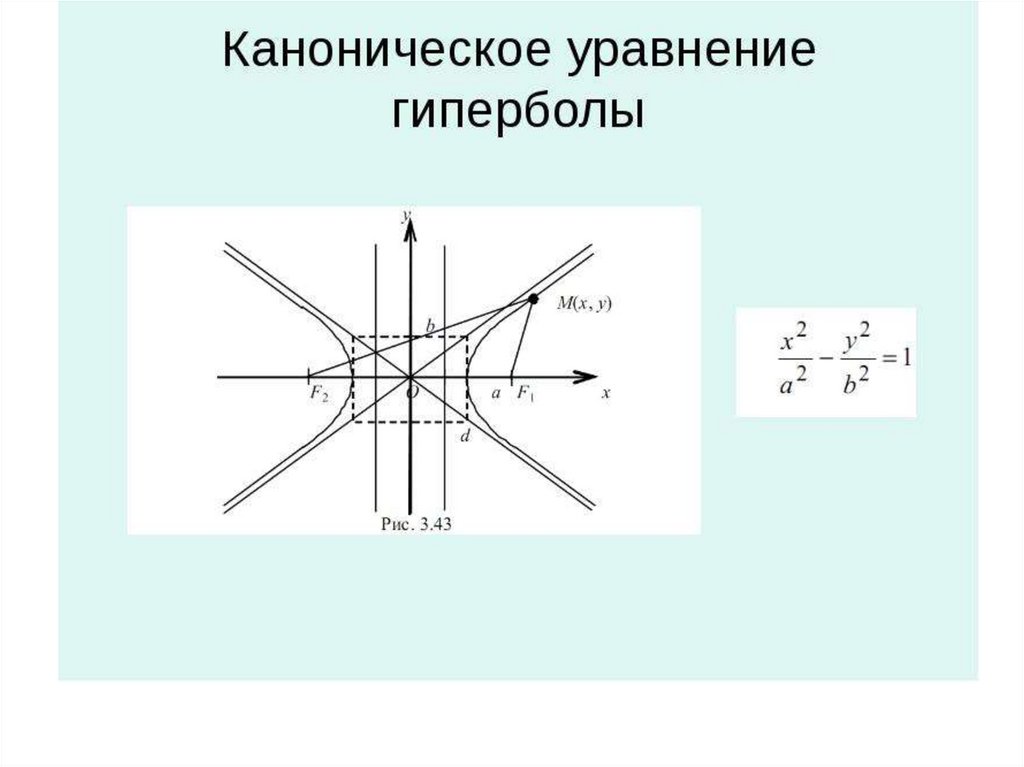
Используйте калькуляторы или специальные программы для более быстрого нахождения параметров гиперболы, если необходимо.
Если гипербола не проходит через начало координат, проверьте, есть ли сдвиг осей — это может повлиять на результаты.

Линии второго порядка на плоскости. Гипербола - Вопрос-ответ 9-

Не забывайте про асимптоты! Это линии, к которым стремится гипербола на больших значениях переменных.
При построении гиперболы важно соблюдать пропорции между осями и правильно выбрать масштаб для более точного изображения.

Видеоурок \
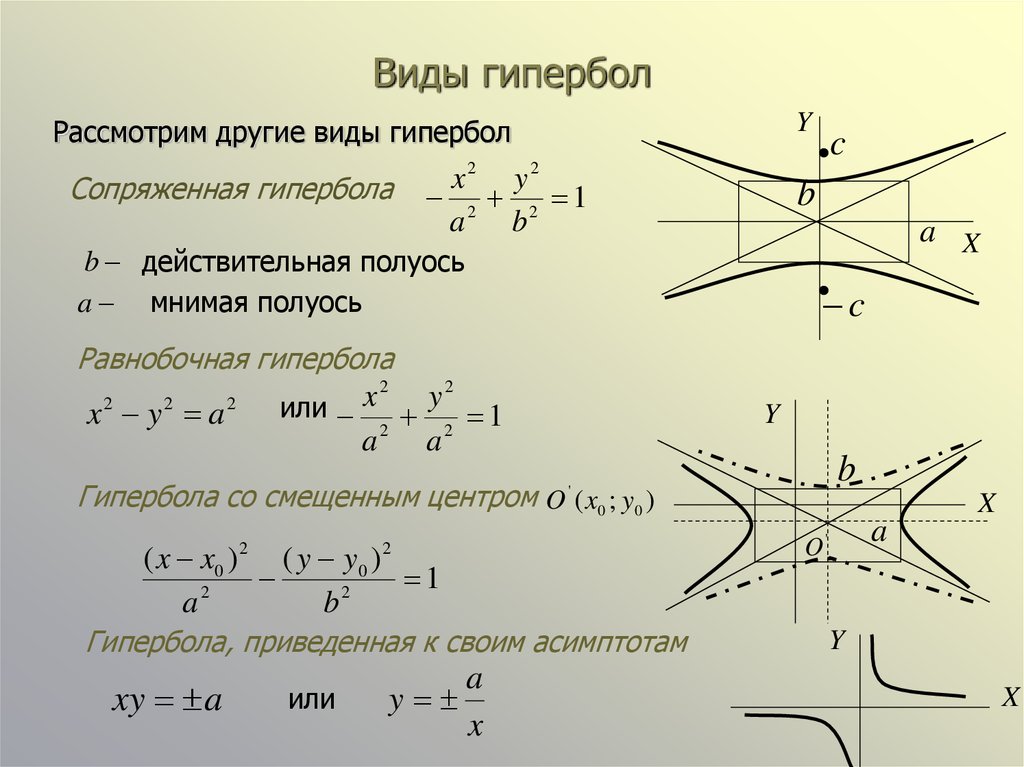
Обратите внимание на эксцентриситет гиперболы, который дает представление о ее степени «растяженности» и влияния на форму построения.


Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математика