Полезные советы по нахождению высоты из основания равнобедренного треугольника
Высота из основания равнобедренного треугольника играет важную роль в расчетах геометрических параметров. Она определяет положение вершины относительно основания и часто используется для нахождения площади треугольника. Важно точно вычислять эту высоту для выполнения задач в геометрии и архитектуре. На этой странице вы найдете полезные советы, которые помогут вам правильно вычислить высоту, используя различные методы и подходы.
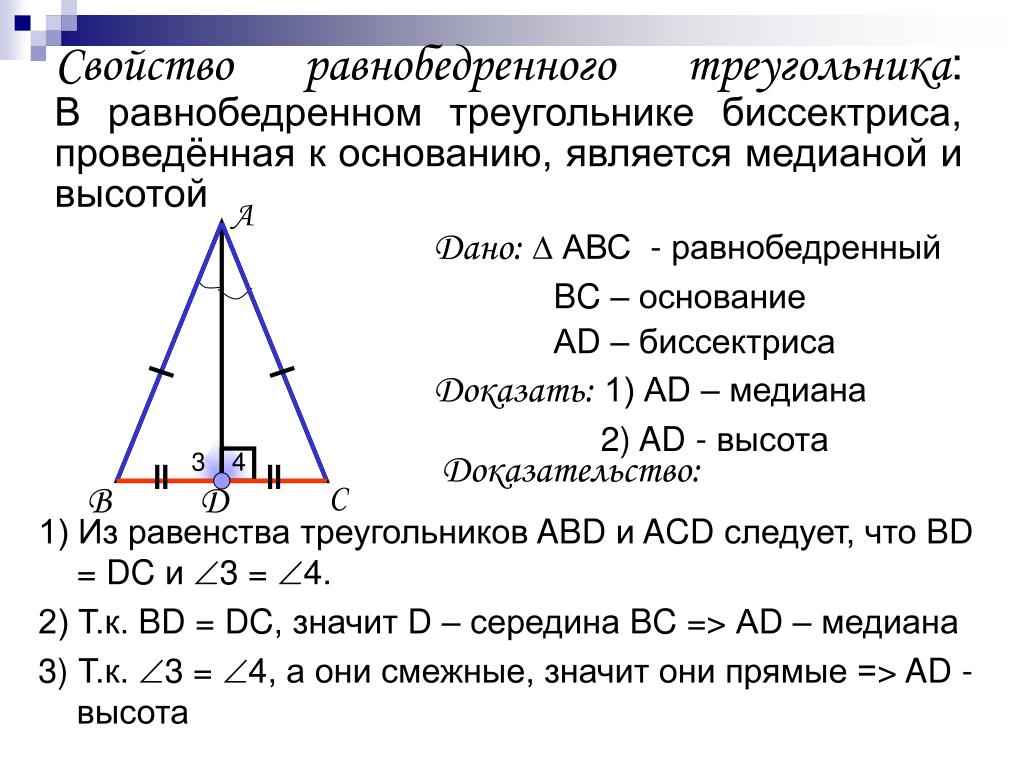

Для нахождения высоты из основания равнобедренного треугольника используйте формулу: h = √(a² - (b/2)²), где a — длина равных сторон, а b — длина основания.
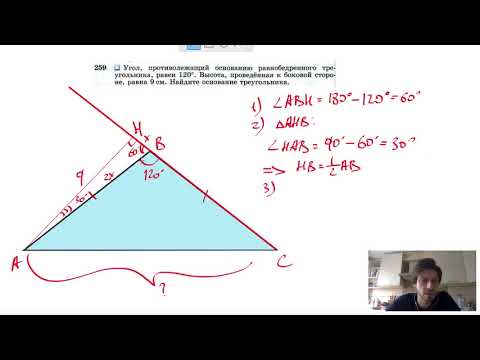
№259. Угол, противолежащий основанию равнобедренного треугольника, равен 120°. Высота, проведенная
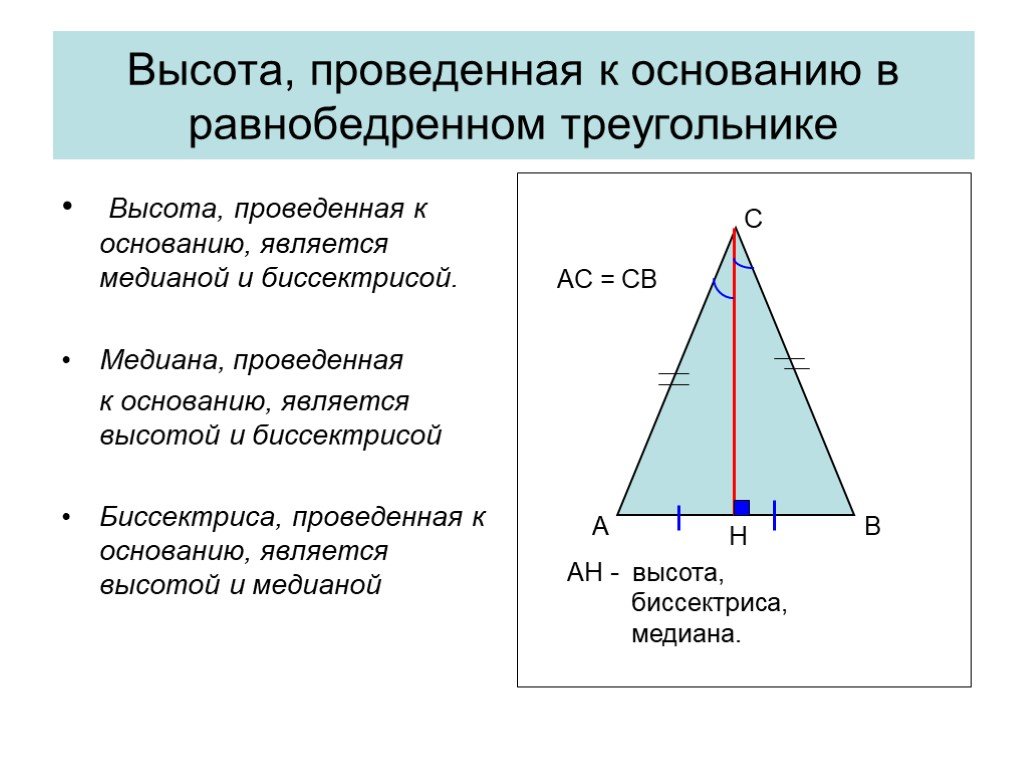

При построении чертежей обязательно помечайте высоту и основание, чтобы избежать ошибок в расчетах.
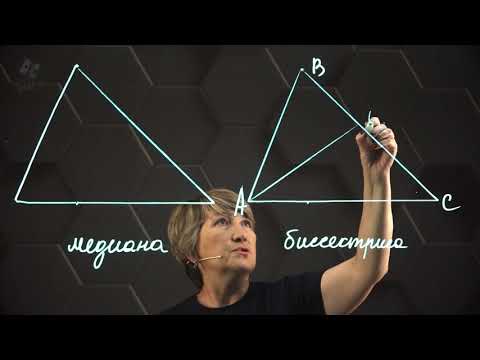
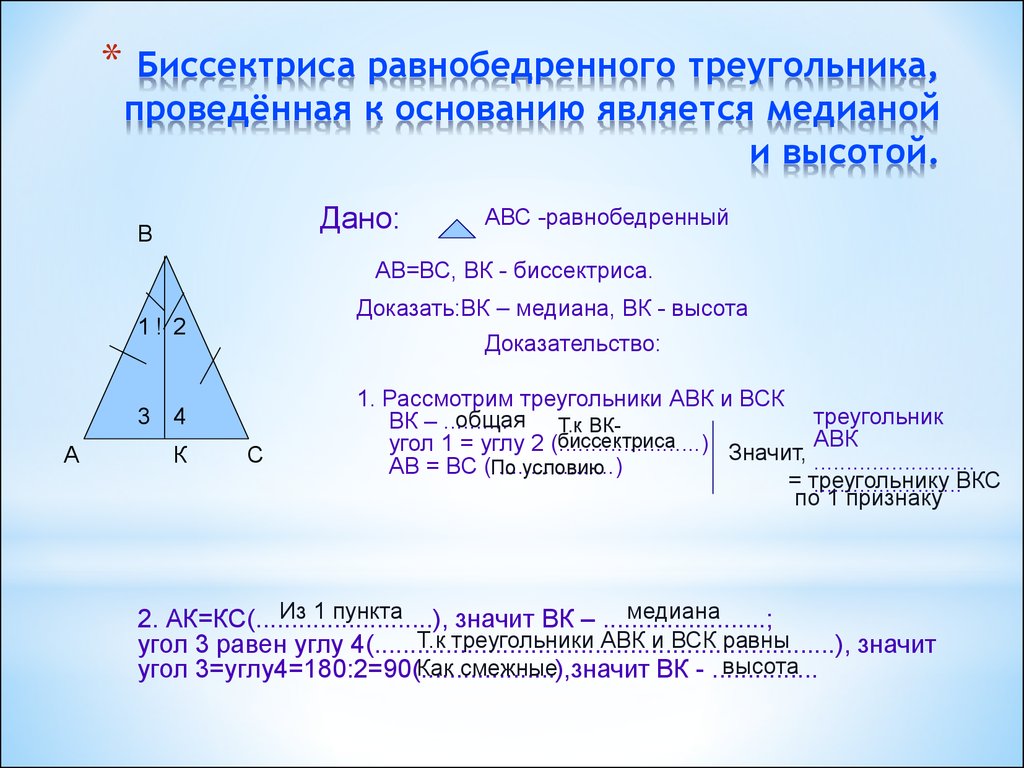
Высота, биссектриса, медиана. 7 класс.
Если вам нужно найти площадь равнобедренного треугольника, используйте формулу площади: S = 1/2 * b * h, где b — основание, h — высота.
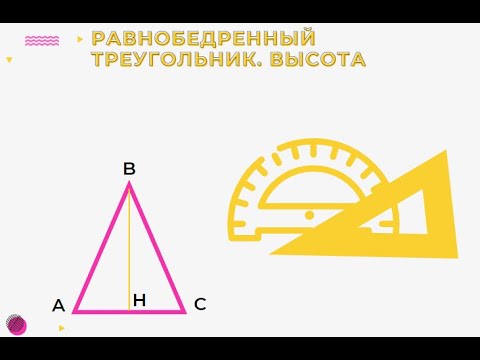
Урок 5. Равнобедренный треугольник. Высота.
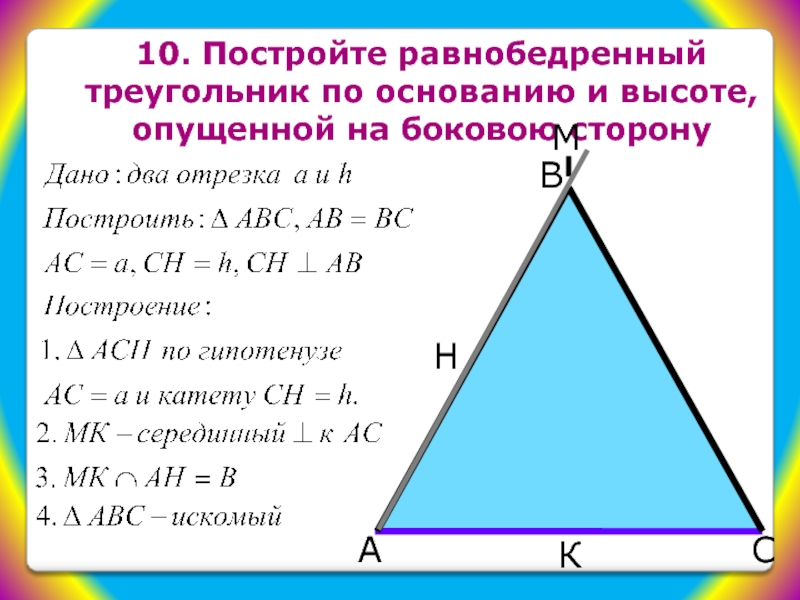
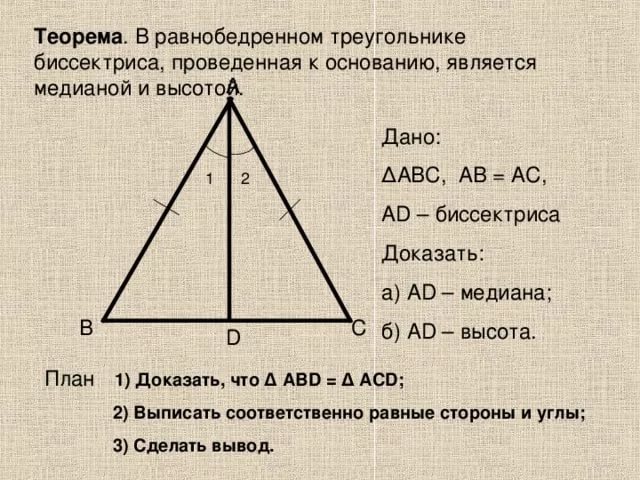
Для визуального понимания высоты из основания, можно провести перпендикуляр от вершины треугольника к основанию, что поможет определить его точное местоположение.

Равнобедренный треугольник. Свойства равнобедренного треугольника - Математика - TutorOnline

Помните, что высота из основания равнобедренного треугольника всегда будет делить основание пополам, что упрощает вычисления.

7 класс, 18 урок, Свойства равнобедренного треугольника


Используйте графические методы, такие как построение высоты на бумаге или в графических редакторах, для более точных расчетов.

Если известны только углы треугольника и одна сторона, высоту можно найти через синус угла с помощью тригонометрических функций.

Свойства равнобедренного треугольника. 7 класс.

Не забывайте учитывать единицы измерения при вычислениях, чтобы результат был точным и соответствовал нужной системе.

Геометрия. 7 класс. Теоремы. Т6. Второе свойство равнобедренного треугольника.
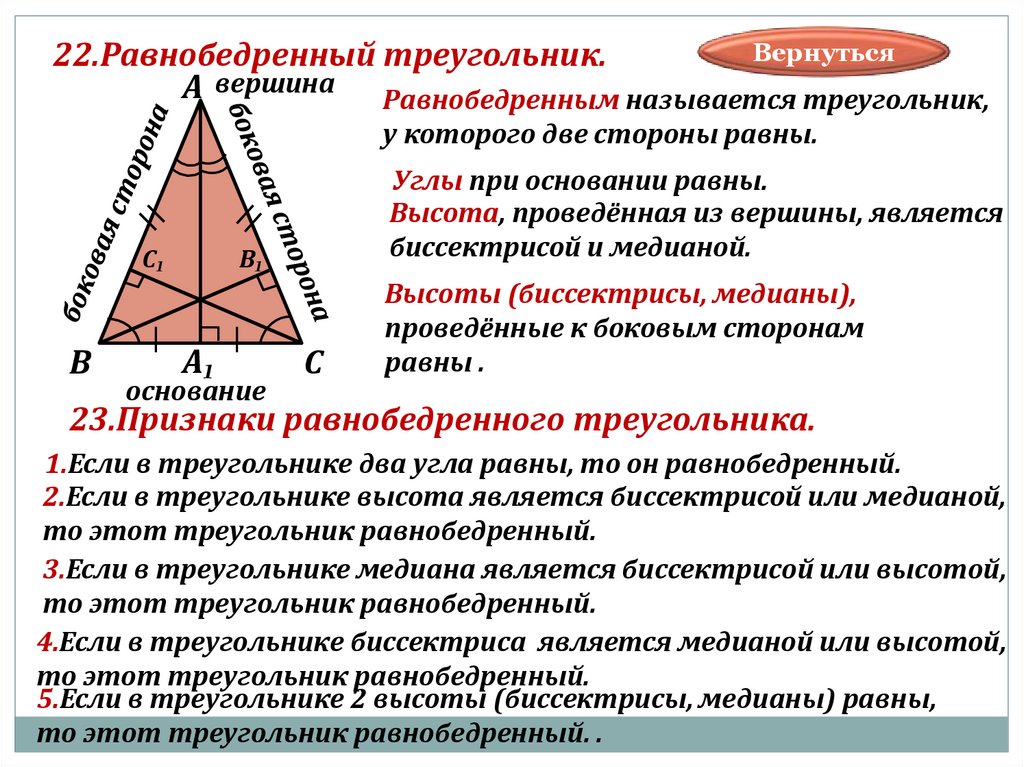
В некоторых случаях для нахождения высоты может быть полезно разложить треугольник на два прямоугольных треугольника и использовать теорему Пифагора.

Всегда проверяйте результат, подставляя вычисленную высоту обратно в формулы для площади или других параметров треугольника.
