Особенности деления большего основания трапеции высотой: советы и рекомендации
На этой странице вы найдете подробное объяснение того, как высота трапеции делит ее большее основание на два отрезка. Мы расскажем, почему это свойство важно для решения задач и как правильно использовать его при расчетах. Также вас ждут полезные советы и рекомендации для правильного понимания этой геометрической особенности.


Чтобы правильно делить основание трапеции, всегда четко определяйте, какая из сторон является большей. Это поможет избежать ошибок при вычислениях.
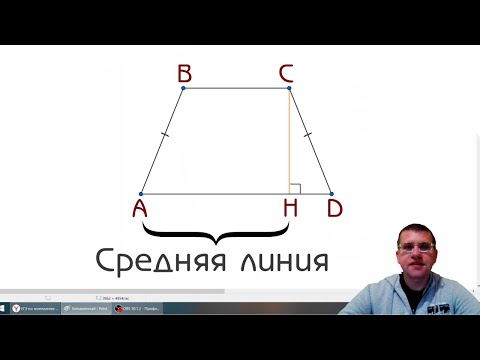
На какие отрезки делит высота в равнобедренной трапеции большее основание ?

Обратите внимание, что высота трапеции всегда перпендикулярна основанию. Это важно для правильного применения теоремы о делении основания.

Многоугольники. Четырехугольники. Трапеция и ее средняя линия. Сборник тестов. DİM 2023.
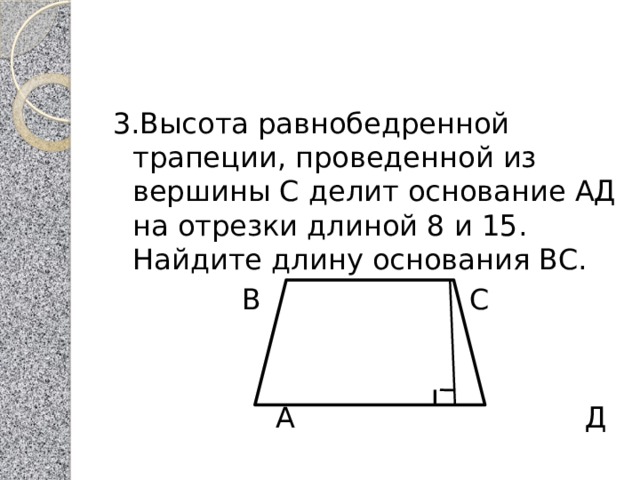

Не забывайте, что длина отрезков, на которые делится основание трапеции, может быть найдена с помощью пропорций, если другие параметры трапеции известны.
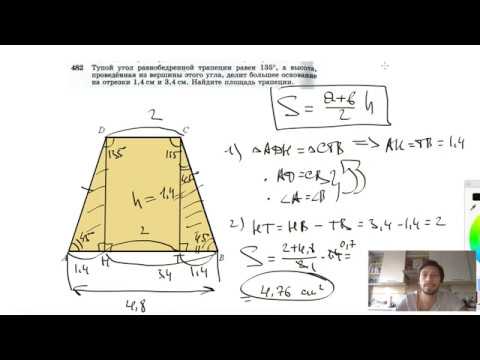
№482. Тупой угол равнобедренной трапеции равен 135°, а высота, проведенная из вершины этого угла,

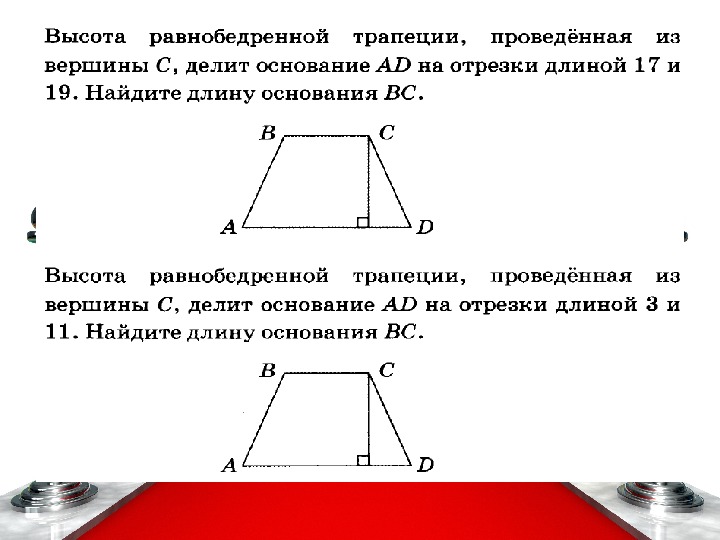
Используйте понятие средней линии трапеции для упрощения расчетов, если вам нужно вычислить отношения между отрезками основания.
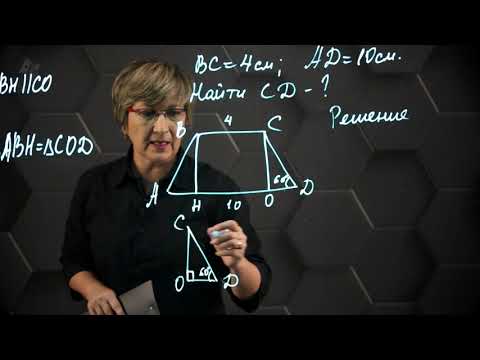
Трапеция. Практическая часть - решение задачи. 8 класс.

Для практики попробуйте решать задачи, где основание трапеции делится высотой на отрезки, это поможет вам лучше понять принцип.

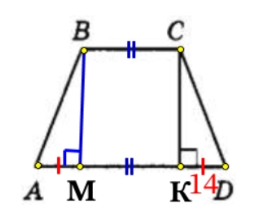
Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит
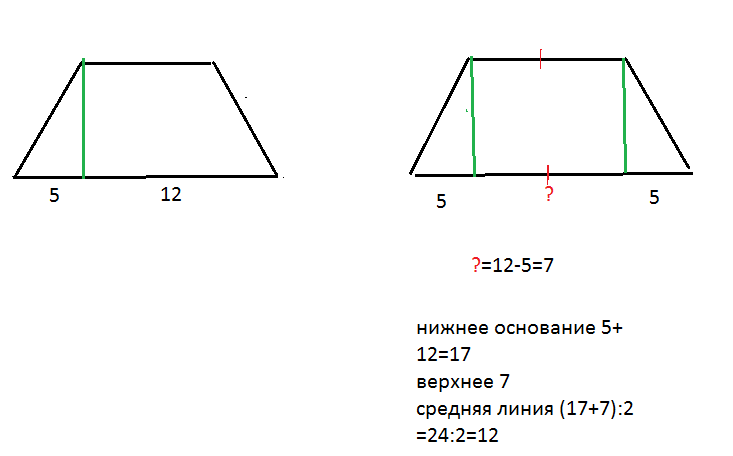
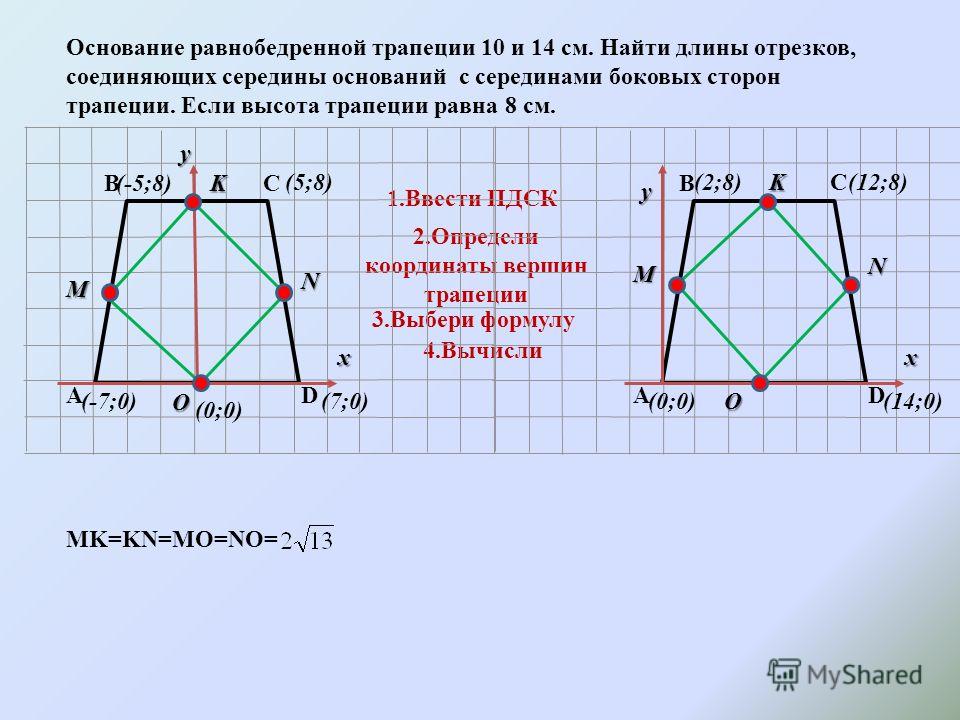
При решении задач с трапециями не забывайте о взаимосвязи между высотой, основаниями и боковыми сторонами, так как они часто используются для нахождения других элементов фигуры.

Помните, что при делении основания трапеции на отрезки важно учитывать все параметры фигуры, чтобы избежать ошибок при дальнейших вычислениях.
Если вам нужно быстро вычислить длину одного из отрезков, используйте формулы, которые дают прямое соотношение между высотой и длинами сторон трапеции.

Вписанная и описанная трапеции. Классика
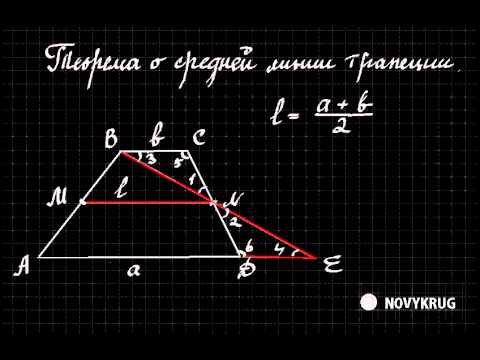
Теорема о средней линии трапеции

Применяйте методы интеграции и аналогии для решения сложных задач с трапециями, если прямые вычисления оказываются трудными.

Высота AH ромба ABCD делит сторону CD на отрезки DH = 20 и CH = 5. Найдите высоту ромба.
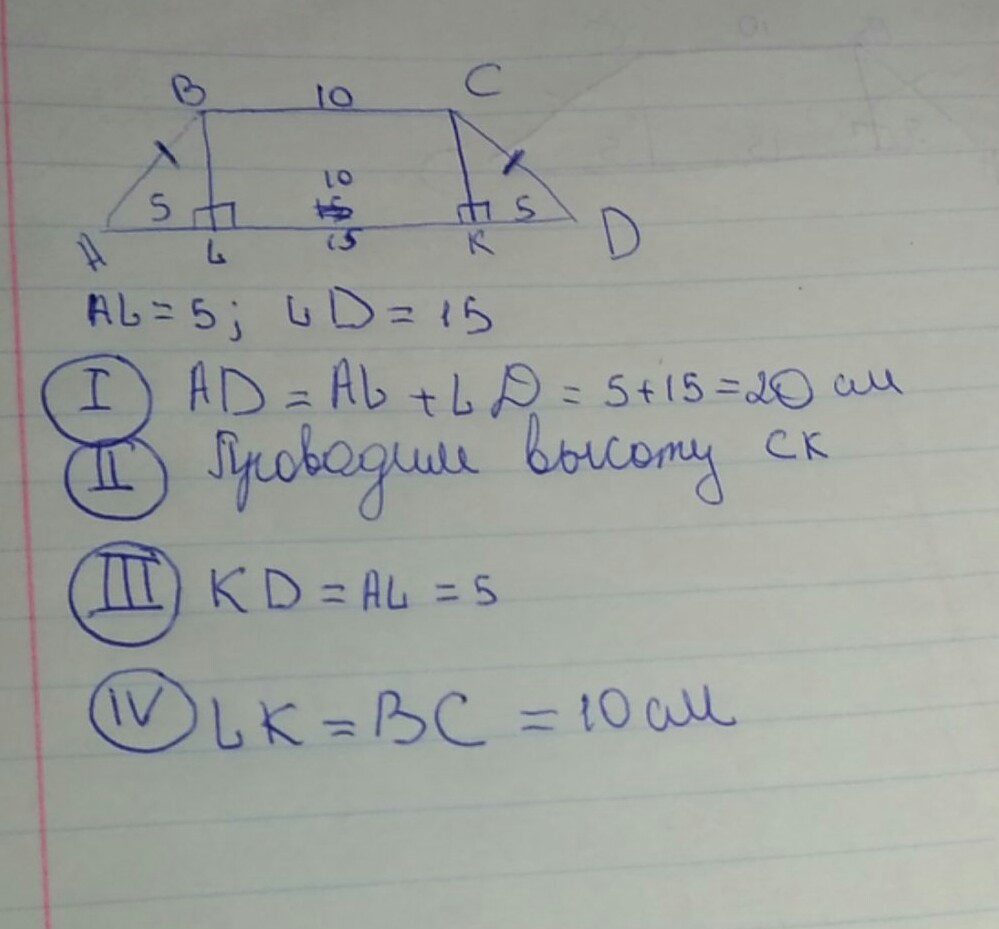

Чем больше задач вы решаете, тем легче вам будет воспринимать и применять основные свойства трапеции в геометрии.

