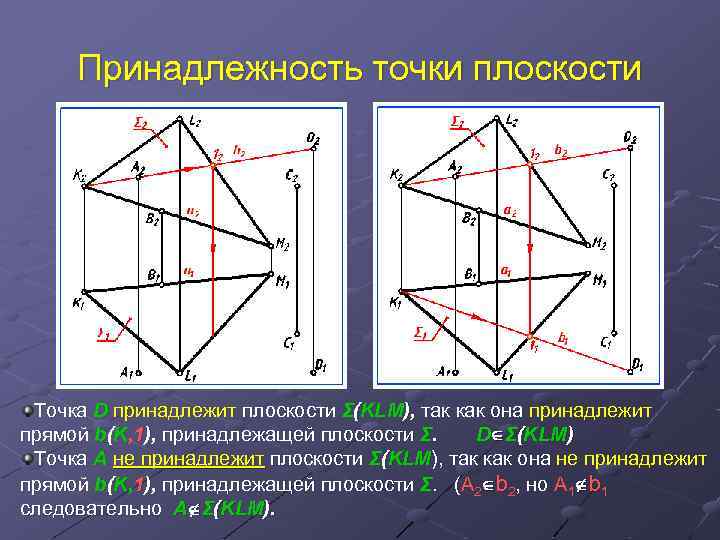
Методы проверки принадлежности точки плоскости в геометрии: советы и решения
В этой подборке мы рассмотрим основные методы и формулы для определения принадлежности точки плоскости, а также полезные советы для эффективного применения этих знаний в решении задач. Эта информация будет полезна как студентам, так и профессионалам, работающим с геометрией.


Для определения принадлежности точки плоскости часто используют уравнение плоскости, полученное из трех точек, принадлежащих этой плоскости.
Алгоритмы развётвлённой структуры в С++. If, Else. Лабораторная работа №2. Попадёт ли точка?

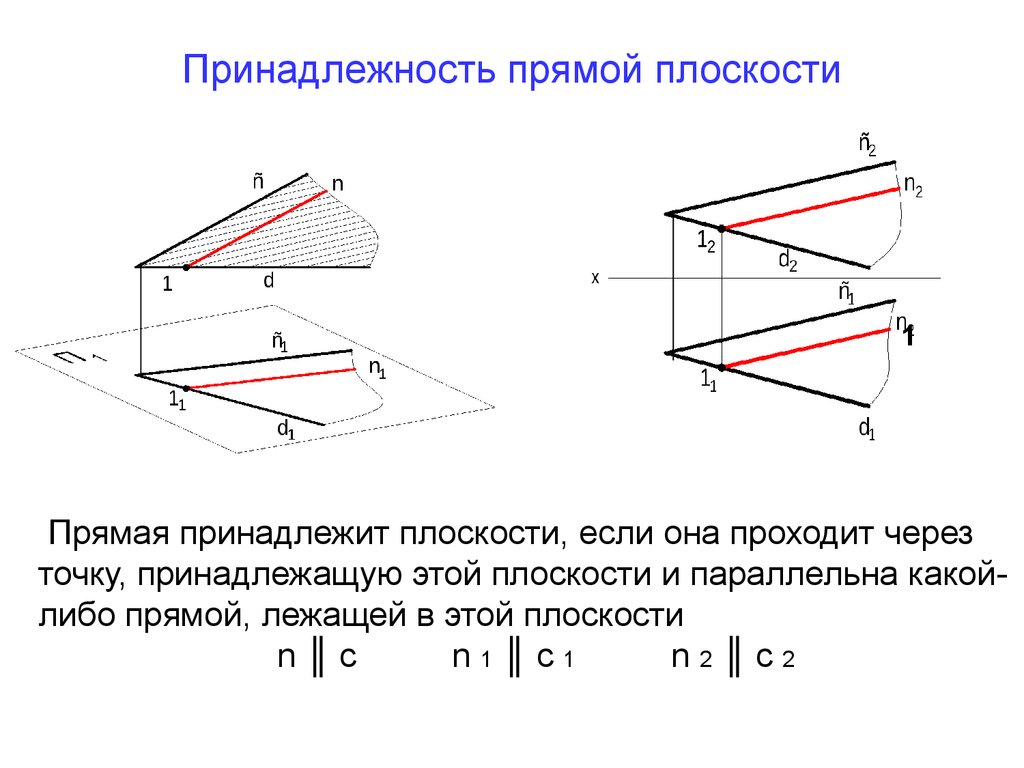
Важно помнить, что если координаты точки удовлетворяют уравнению плоскости, то точка лежит на этой плоскости.

Самый короткий тест на интеллект Задача Массачусетского профессора
При анализе задачи всегда проверяйте, все ли данные о точках и плоскости заданы корректно, чтобы избежать ошибок в вычислениях.

ТЕМА 1. ОСНОВЫ ПЕРСПЕКТИВЫ
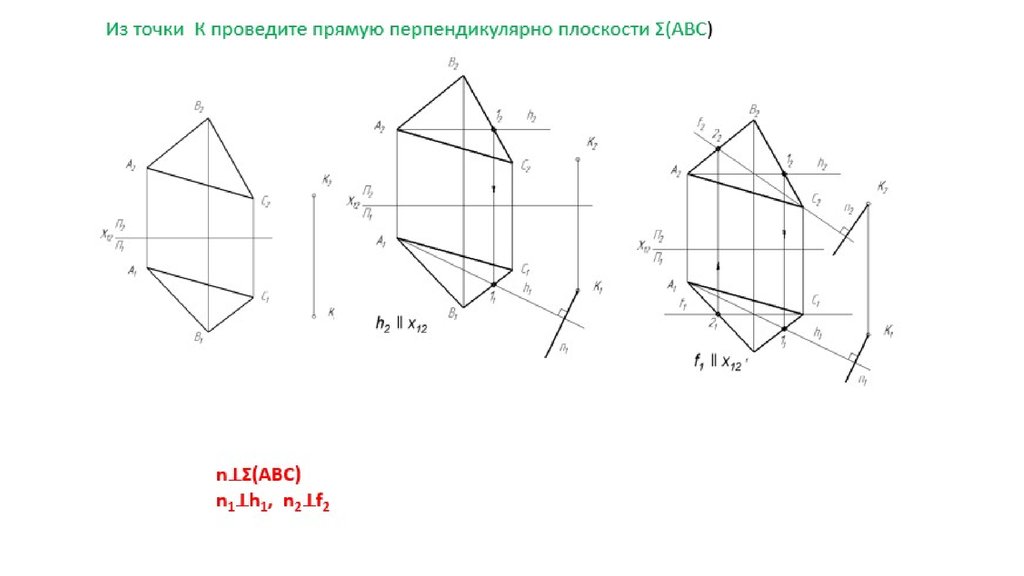
Для выполнения более сложных задач полезно использовать метод векторного произведения, чтобы проверить, лежит ли точка на плоскости, заданной двумя векторами.

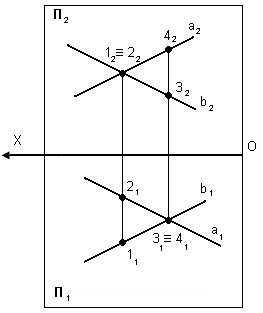
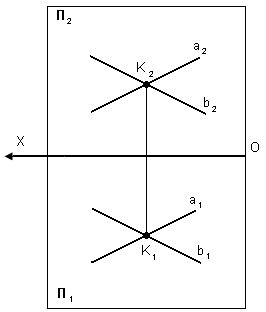
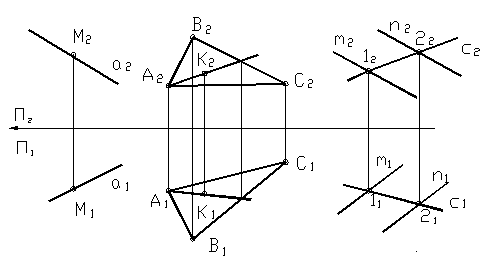
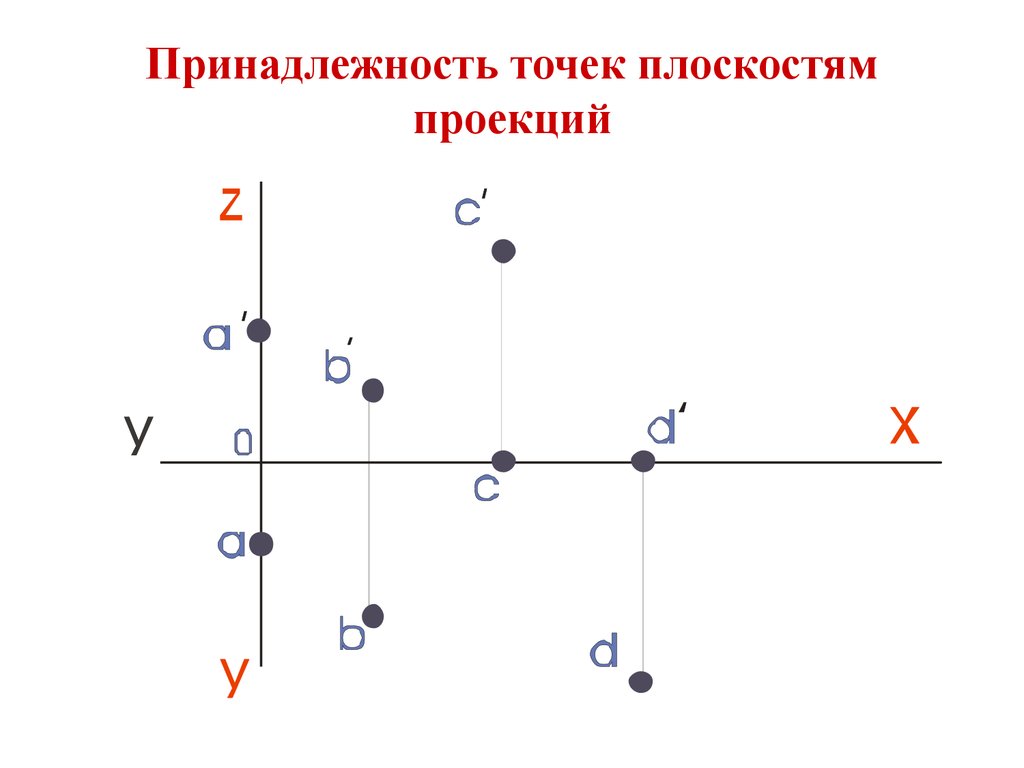
Частное положение точек. Точки принадлежащие к плоскостям проекции.
Не забывайте, что плоскость в трехмерном пространстве можно задать как уравнение вида Ax + By + Cz + D = 0.

Лекция 2. Основная задача начертательной геометрии. Точка пересечения прямой с плоскостью.

При работе с системой уравнений для проверки принадлежности точки плоскости важно правильно учитывать все переменные и не упускать детали в расчетах.
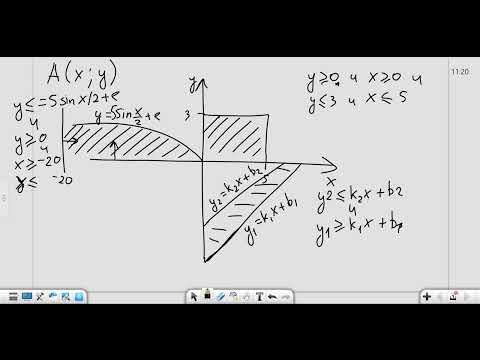
Принадлежность точки закрашенной области
Если у вас есть график, то можно визуально проверить расположение точки относительно плоскости, но для точных расчетов лучше использовать аналитические методы.

Квантовая механика: мир, который ты никогда не поймешь - Level One
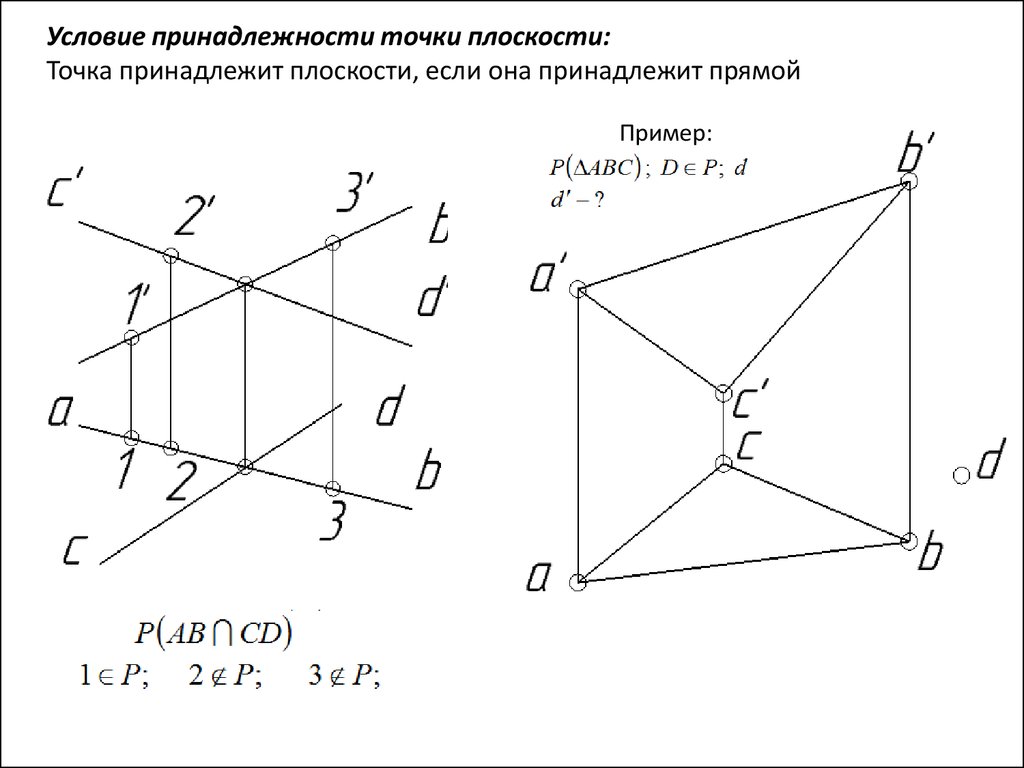
Для оптимизации решения задач рекомендуется научиться быстро и точно работать с координатами точек и уравнениями плоскости в различных системах координат.

Принадлежность прямой плоскости
При использовании различных методов всегда старайтесь выбрать самый простой и быстрый способ, который минимизирует количество операций.

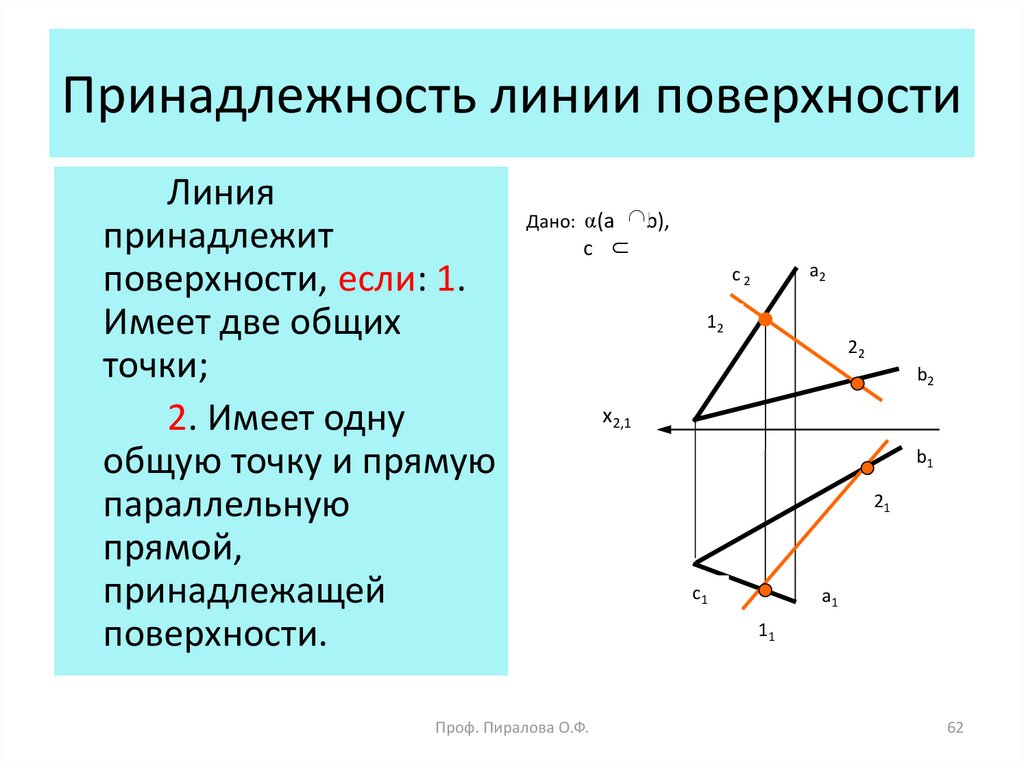
Построение недостающей проекции плоскости. Принадлежность прямой к плоскости
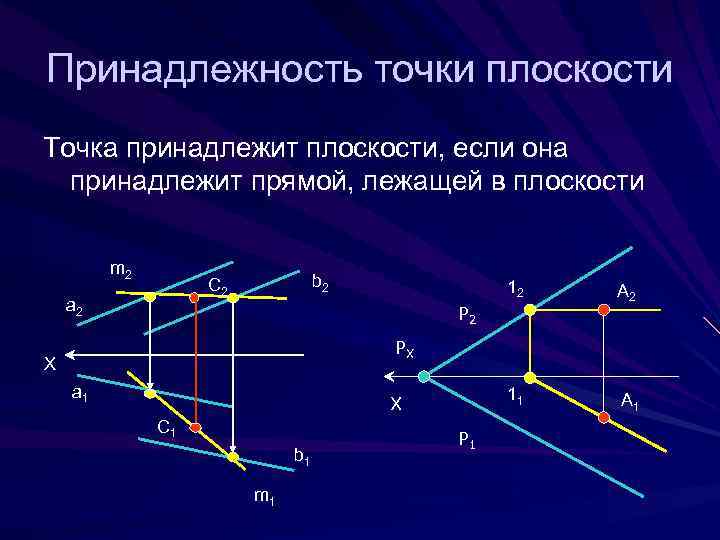
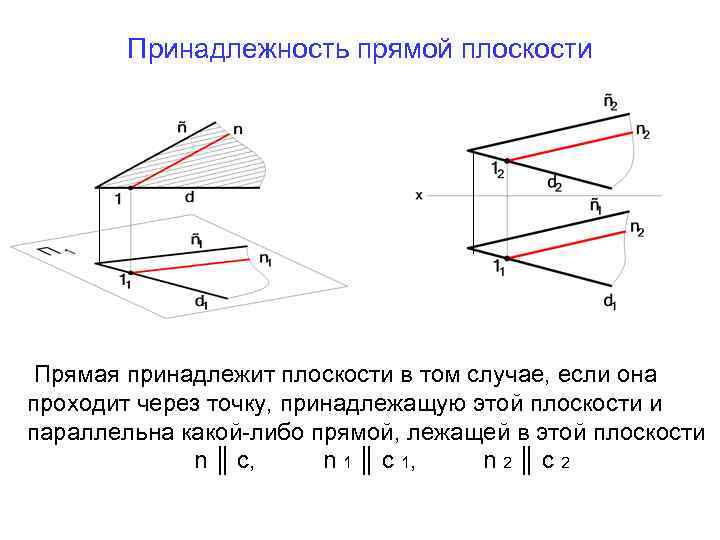
Помните, что задача на принадлежность точки плоскости может быть частью более сложных задач, требующих комплексного подхода и знаний других разделов геометрии.
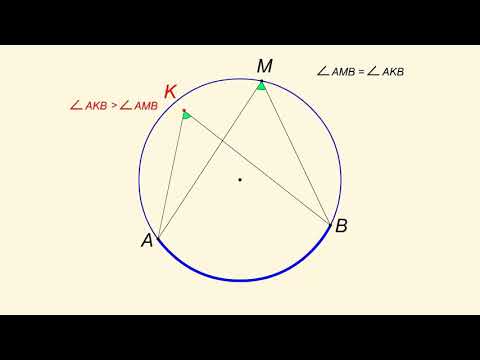
Первое условие принадлежности четырех точек одной окружности