Полное объяснение нахождения уравнения касательной через вычисление производной функции
В этой статье мы подробно рассмотрим, как с помощью производной можно найти уравнение касательной к графику функции в точке касания. Пошаговые инструкции помогут вам освоить этот важный математический процесс, который используется в различных областях науки и техники.


Для нахождения уравнения касательной необходимо вычислить производную функции в точке касания.

Геометрический смысл производной - Касательная

Не забудьте, что для точности расчётов нужно правильно найти координаты точки касания на графике функции.

Производная с нуля. Решаем 100+ задач из сборника Демидовича. Высшая математика

Производная функции в точке касания определяет угловой коэффициент касательной прямой.
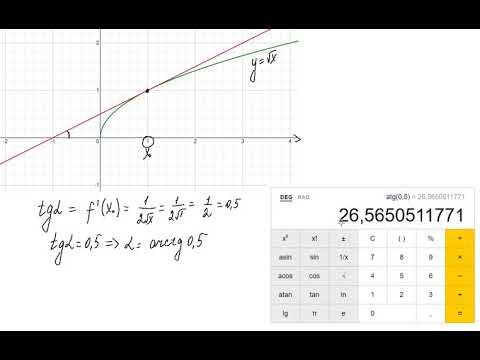
Геометрический смысл производной. Угол наклона касательной. Уравнение касательной


Уравнение касательной можно записать в виде y = f(x0) * (x - x0) + f(x0), где x0 — это абсцисса точки касания.

Математика без Ху%!ни. Уравнение касательной.
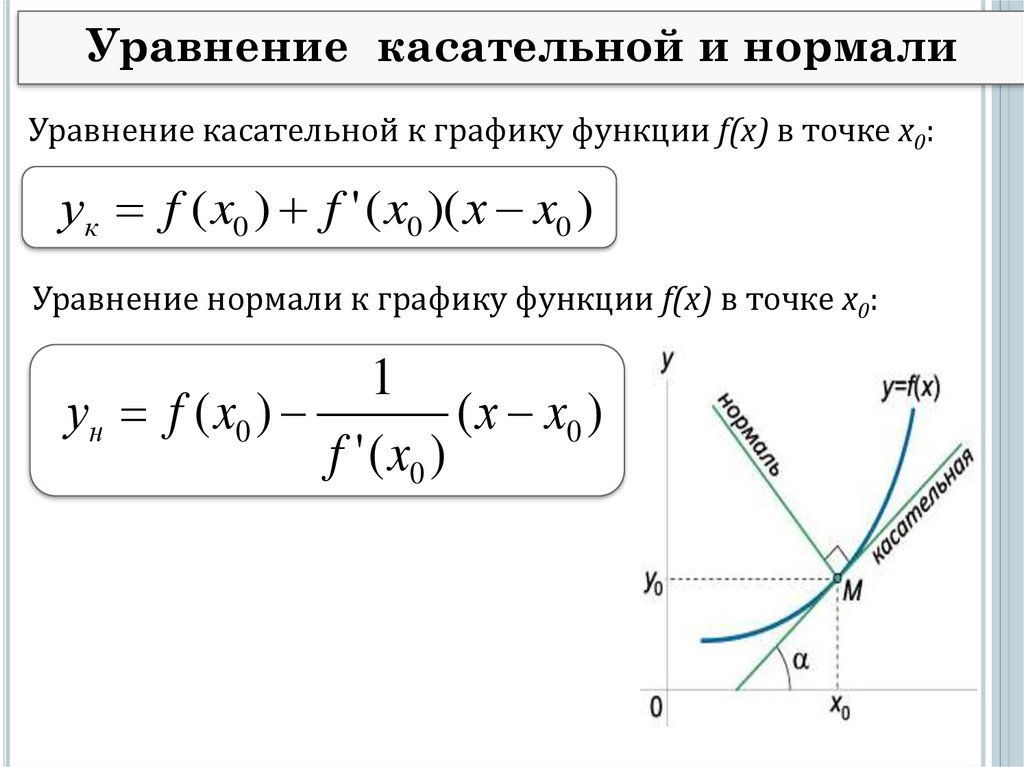
Если функция имеет несколько экстремумов, для каждого из них нужно находить касательные отдельно.
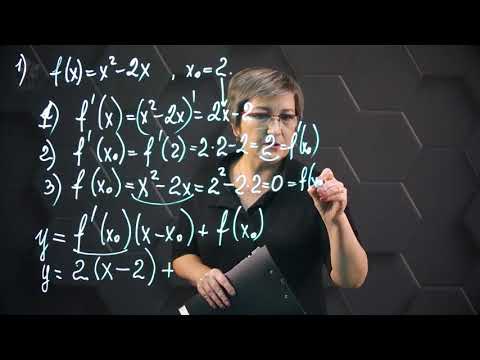
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.

При работе с производной важно помнить о правилах дифференцирования для различных типов функций (например, для степенных или тригонометрических функций).

10 класс, 43 урок, Уравнение касательной к графику функции

Графически можно изобразить касательную как прямую, которая пересекает график функции только в одной точке.
Для получения точных результатов обязательно учитывайте особенности поведения функции в окрестности точки касания.


Если функция не дифференцируема в точке, то касательная прямая не существует.

Производные: Уравнение Касательной

Уравнение касательной можно использовать для анализа поведения функции вблизи точки касания, что важно для математического моделирования.
