Как эффективно изучать свойства многочленов
На этой странице вы найдете подборку фотографий и полезных советов для изучения теории многочленов, включая основные принципы, примеры применения и практические рекомендации.


Начните с изучения основных понятий: степени многочлена, коэффициентов и корней.

Тимашёв Д. А. - Алгебра. Часть 1 - Теорема Безу, схема Горнера, алгоритм Евклида для многочлена

Практикуйте разложение многочленов на множители для лучшего понимания структуры.
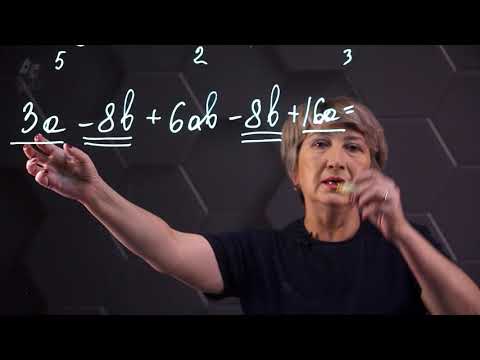
Многочлены. 7 класс.
Используйте графики, чтобы визуализировать поведение многочленов.

А Зухба, Теория групп, Видео 24: Неприводимые многочлены


Обратите внимание на свойства симметрии и знаков коэффициентов.

Теорема Безу. 10 класс.
Изучите методы деления многочленов, включая схему Горнера.

38 Кольцо многочленов

Регулярно решайте задачи на нахождение корней уравнений.

Теория колец и полей 7. Кольцо многочленов. Неприводимые многочлены. Расширение поля


Исследуйте связи между корнями и коэффициентами с помощью теоремы Виета.


Используйте программное обеспечение, например, WolframAlpha или GeoGebra, для проверки расчетов.

Многочлен и его стандартный вид. Алгебра, 7 класс

Чередуйте теорию с практикой, чтобы лучше закрепить материал.

LEC-12,UFD's, GAUSS LEMMA,EISENSTEIN's CRITERION,POLYNOMIAL RINGS,REDUCIBLE,IRREDUCIBLE POLYNOMIALS


Изучайте примеры реальных применений многочленов в физике и экономике.


Схема Горнера. Объяснение на пальцах. Деление многочленов