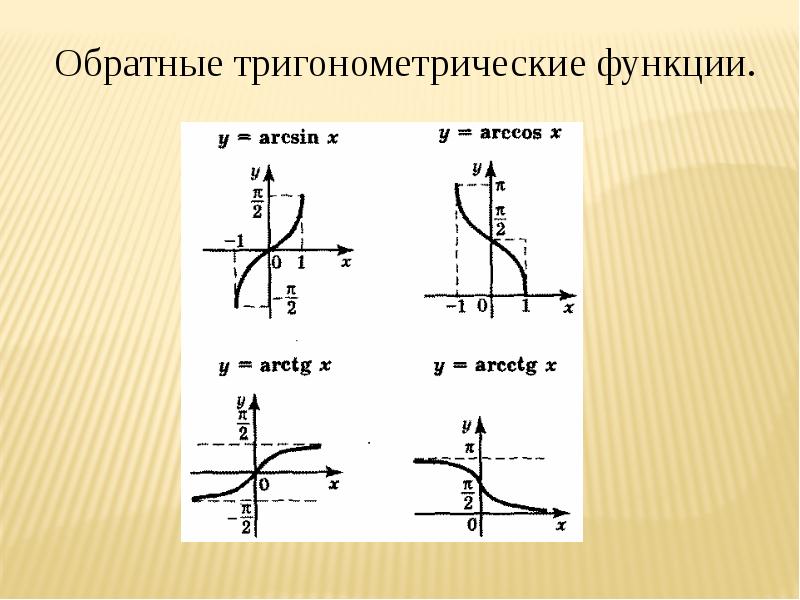
Основные свойства и применение обратных тригонометрических функций
Подробный обзор свойств обратных тригонометрических функций с наглядными примерами, графиками и полезными советами для лучшего понимания темы.


Обратные тригонометрические функции определяются для ограниченного множества значений.

19 Свойства обратных тригонометрических функций


Изучите основные формулы для арксинуса, арккосинуса и арктангенса, чтобы упростить их применение.

Арк-функции. Простейшие тригонометрические уравнения - Осторожно, спойлер! - Борис Трушин !

Для лучшего понимания используйте графики обратных тригонометрических функций, чтобы видеть их поведение.
Обратные тригонометрические функции, y=arctgx и y=arcctgx, их свойства и графики. 10 класс.

Помните, что арксинус определен в диапазоне от -π/2 до π/2, а арккосинус — от 0 до π.
Обратные тригонометрические функции, y=arcsinx и y=arccosx, их свойства и графики. 10 класс.


В задачах с обратными тригонометрическими функциями проверяйте, чтобы значения попадали в область определения.

Теория обратных тригонометрических функций. Вычисление обратных тригонометрических функций


Используйте свойства четности и нечетности функций для упрощения расчетов.

ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 11 класс ТРИГОНОМЕТРИЯ


Запомните, что арктангенс и арккотангенс не определены для ±∞.
Решая уравнения, где используются обратные тригонометрические функции, учитывайте их ограниченные диапазоны значений.

Обратные тригонометрические функции, их свойства и графики. Арксинус. Арккосинус. Билет 2

Для проверки решений используйте обратные преобразования: sin(arcsin(x)) = x, где x находится в области определения.
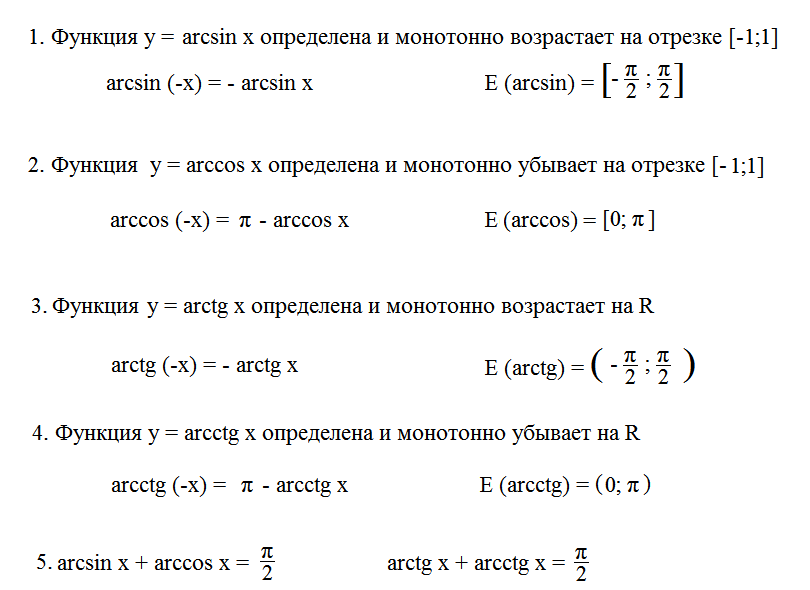

Практикуйтесь на реальных примерах, чтобы лучше освоить свойства и применение этих функций.