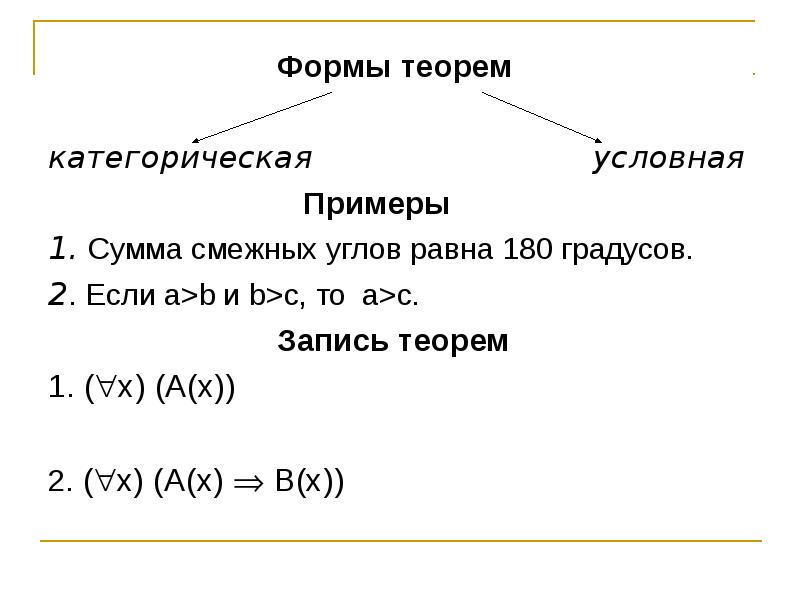
Основные этапы и правила построения теоремы в математических доказательствах
Понимание структуры теоремы — ключевое звено в изучении математики. На этой странице мы разберем основные этапы построения теоремы, ее компоненты и полезные советы, которые помогут не только понять, но и грамотно излагать математические доказательства.

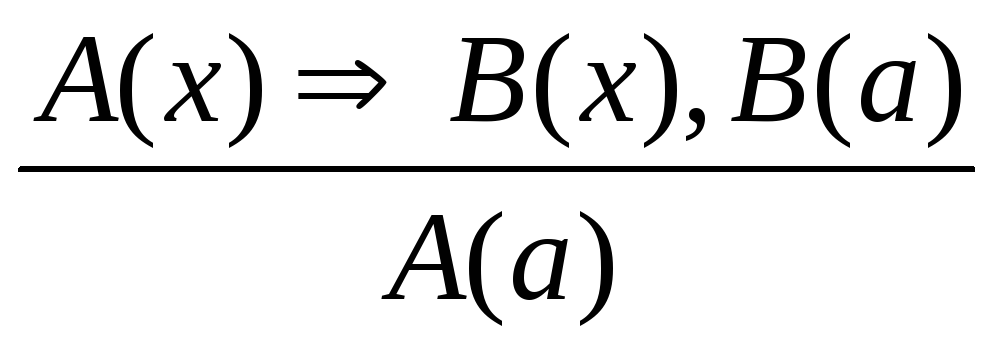
При построении теоремы всегда начинайте с четкой формулировки утверждения, избегайте неясностей и двусмысленностей.

50 САМЫХ ГЕНИАЛЬНЫХ ТЕОРИЙ.

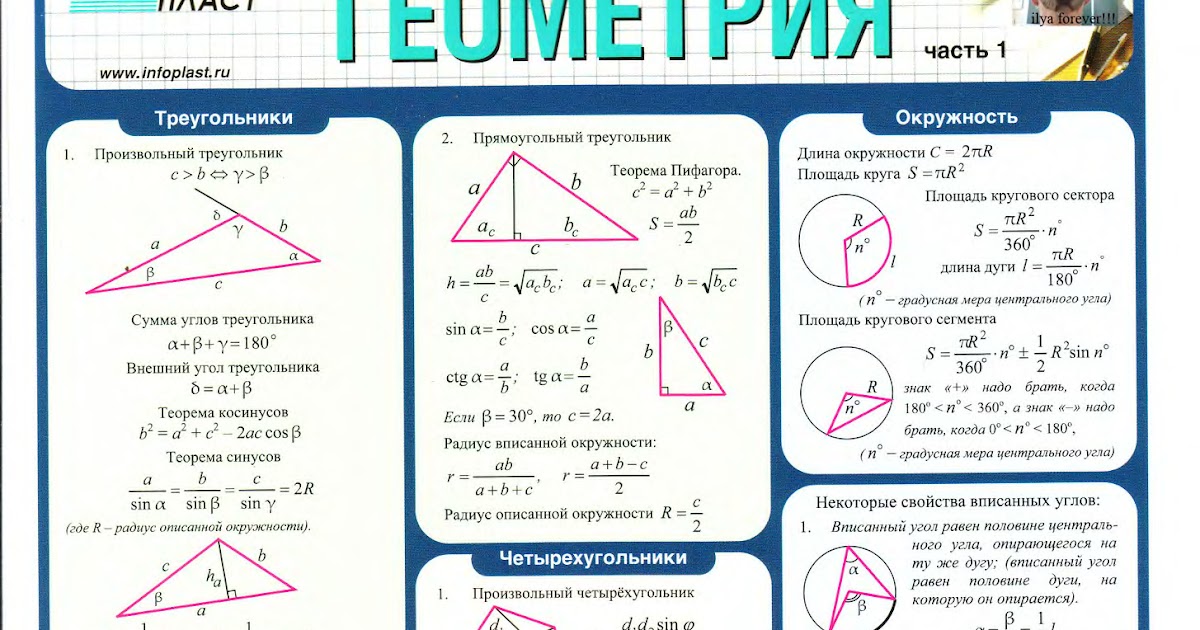
Не забывайте о правильной формулировке гипотезы — от нее зависит логическая структура доказательства.

68. Строение линейного отображения. Алексей Савватеев. 100 уроков математики

Сформулированное утверждение должно быть проверяемым, то есть для него должно существовать доказательство или контрпример.

ФИЗИК Семихатов: Квантовые парадоксы, Мультивселенные, Телепортация, Понять невидимое

Обращайте внимание на логическую последовательность. Доказательство должно строиться шаг за шагом, каждое утверждение должно опираться на предыдущие.

СТРОЕНИЕ АТОМА ХИМИЯ 8 класс // Подготовка к ЕГЭ по Химии - INTENSIV
Используйте математические теоремы и аксиомы в качестве основы для доказательства. Это поможет избежать ошибок и улучшит структуру.

Дмитрий Казаков: \


В каждом доказательстве старайтесь делать акценты на ключевых шагах, чтобы читатель мог следить за логикой.

10 Доказательство Цермело основной теоремы арифметики

Поддерживайте стройность изложения: избегайте сложных фраз и термины объясняйте, если они не являются общеизвестными.

Не забывайте о контексте. Перед доказательством важно обоснование гипотезы, чтобы читатель понимал, что и почему необходимо доказать.
Видеоролик - анимация \

Квантовый мир.

По возможности используйте примеры, чтобы продемонстрировать, как теорема работает на практике.


Проверьте свою теорему на логическую непротиворечивость, чтобы избежать ошибок в формулировке или доказательстве.