Методы вычисления синуса угла между двумя плоскостями для точных расчетов
На этой странице вы найдете полезную информацию и советы по расчету синуса угла между двумя плоскостями. Этот важный аспект геометрии используется в различных областях, от инженерии до физики, и требует точного подхода для достижения правильных результатов. Узнайте, как правильно выполнять расчеты, используя различные методы и формулы.
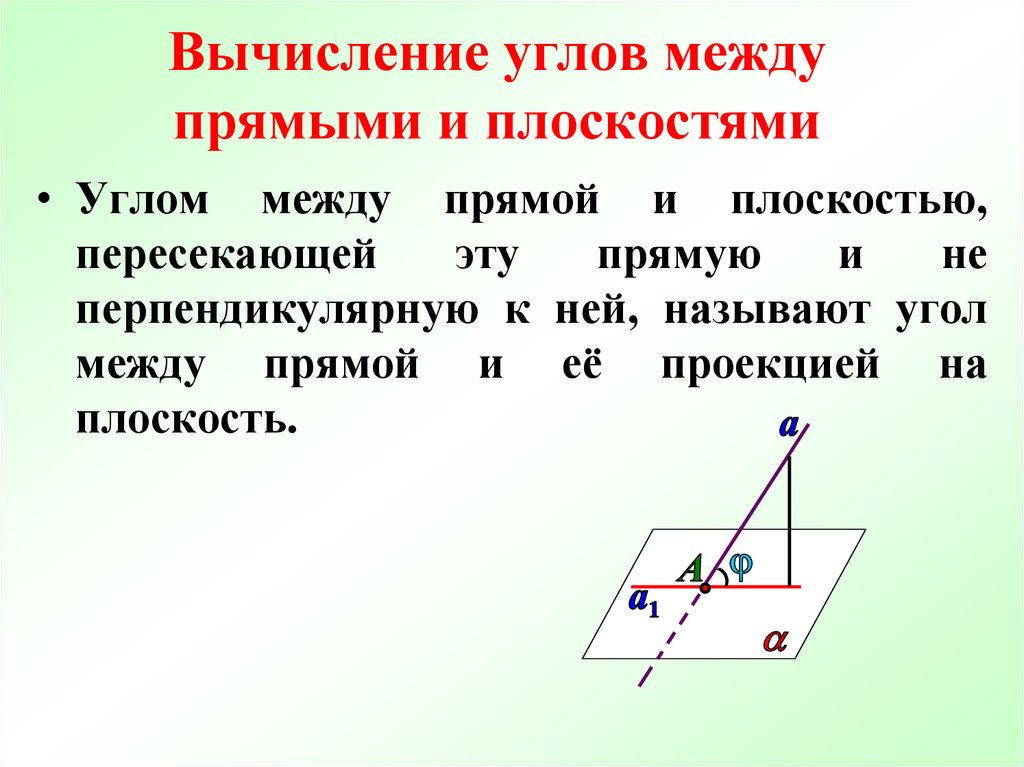
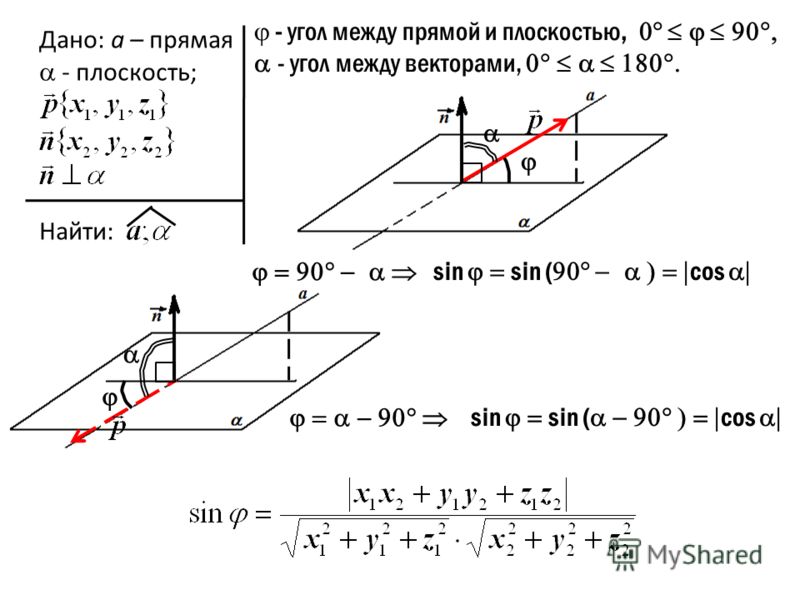
Для расчета синуса угла между двумя плоскостями используйте векторное произведение нормальных векторов этих плоскостей.

ВМ. ШМ. 7.2 Угол между двумя плоскостями. Координаты вершин куба.
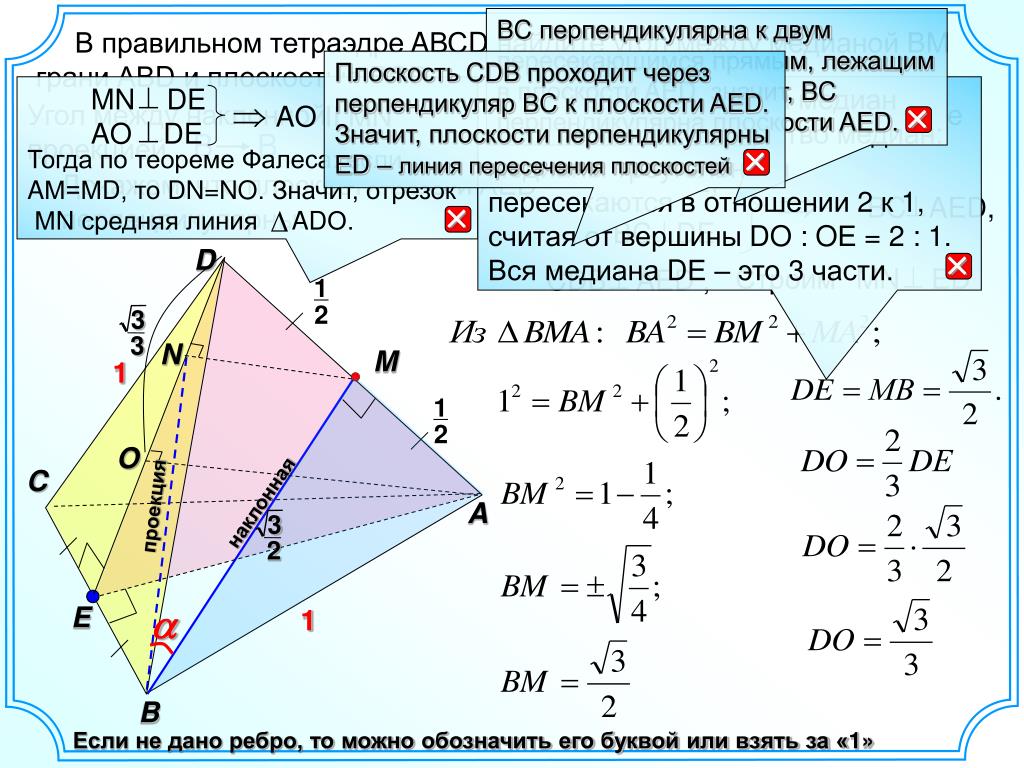
При вычислениях важно сначала найти нормальные векторы обеих плоскостей, так как именно они определяют угол между плоскостями.

Синус, косинус, тангенс, котангенс за 5 МИНУТ

Не забывайте, что синус угла можно вычислить через скалярное произведение нормальных векторов и их длины.

Как найти угол между прямой и плоскостью? СТЕРЕОМЕТРИЯ - TutorOnline

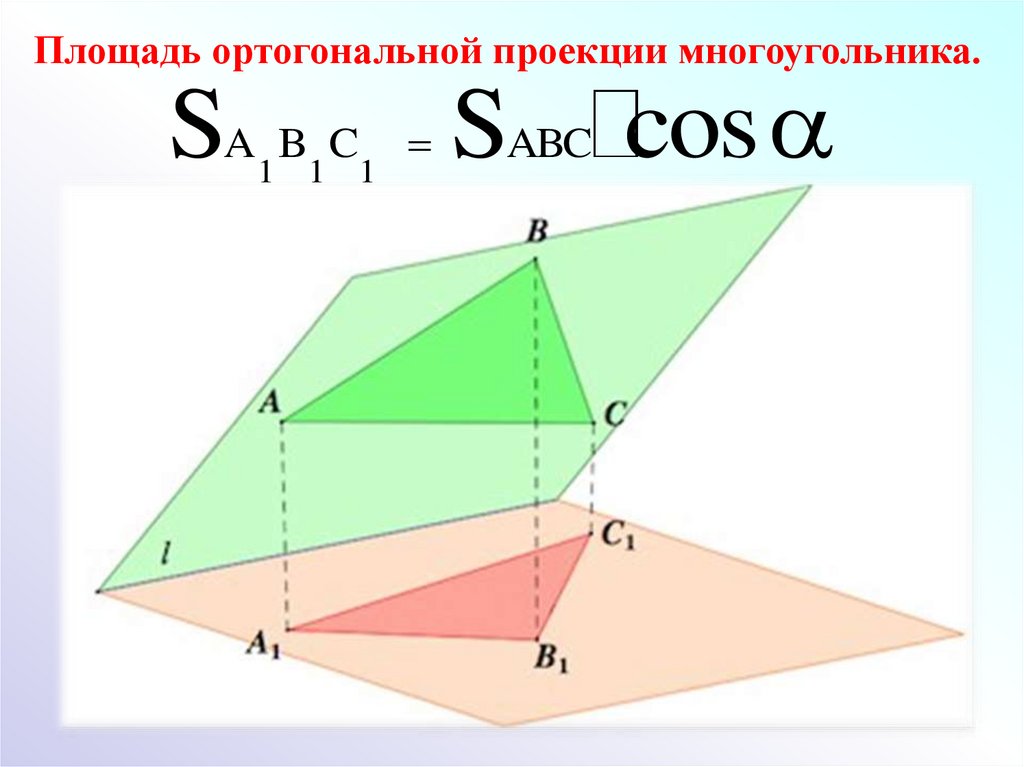
Для точности вычислений используйте систему координат, в которой плоскости заданы уравнениями с известными коэффициентами.

Как найти угол между двумя плоскостями с помощью векторного анализа?
Убедитесь, что нормальные векторы правильно нормализованы, если вы хотите получить синус угла в стандартизированной форме.
Как найти угол между плоскостями
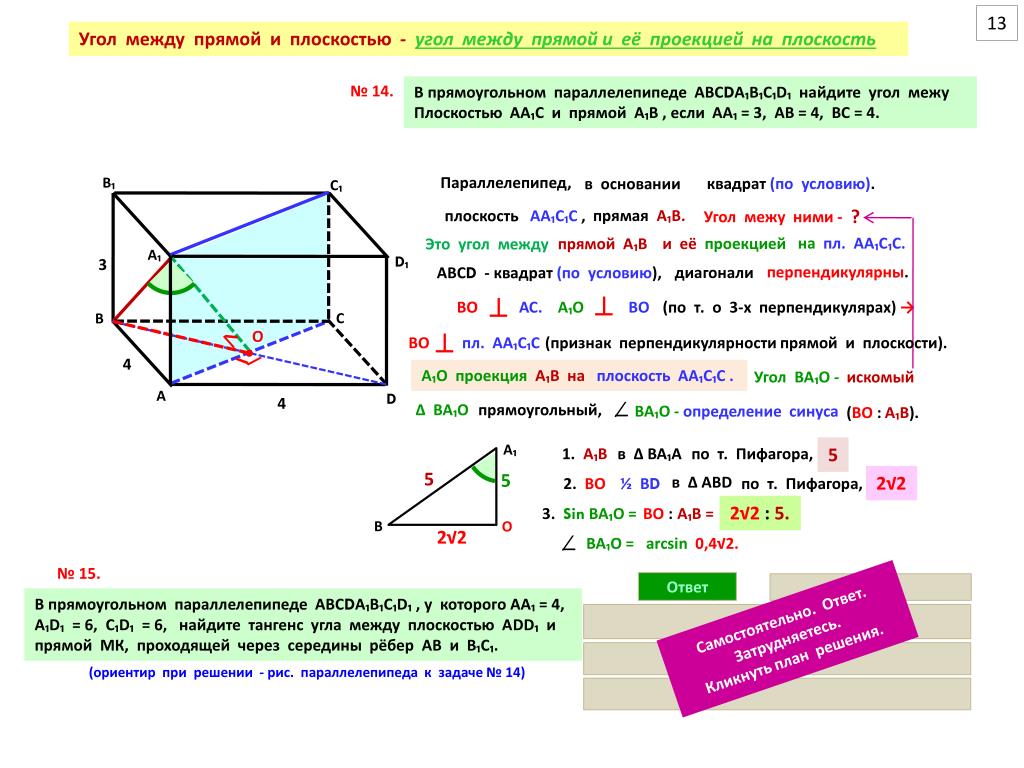
Если угол между плоскостями острый, синус будет положительным, если тупой — отрицательным.

Для вычисления угла между плоскостями используйте формулу: sin(θ) = |(n1 × n2) / (|n1| |n2|)|, где n1 и n2 — нормальные векторы.
В случае использования координатных систем важно учитывать точность числовых значений для минимизации ошибок в расчетах.

Консультация к коллоквиуму по квантовой физике, Глазков В.Н., 07.12.2024

Угол между прямыми, плоскостями, прямой и плоскостью - Математика ЕГЭ для 10 класса - Умскул
Если вы работаете с 3D-графикой или моделированием, точное вычисление углов между плоскостями критично для визуализации и анализа.
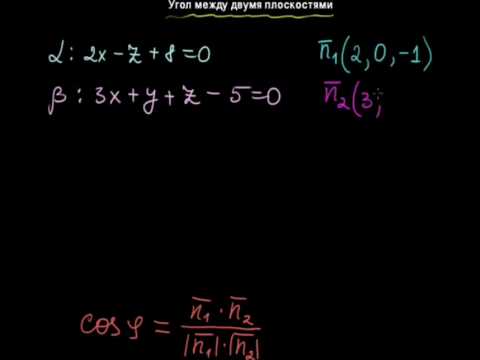
§45 Угол между двумя плоскостями

Чтобы избежать ошибок при расчетах, всегда проверяйте работу с векторами и пересчитывайте все промежуточные шаги дважды.

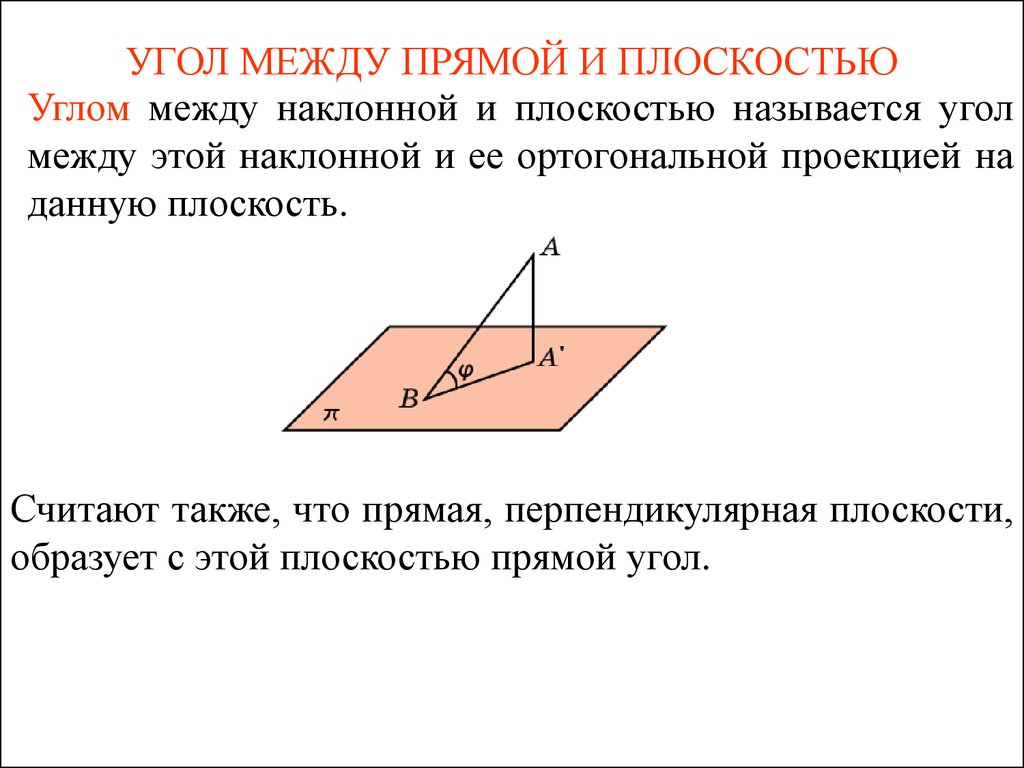

21. Угол между прямой и плоскостью