Как эффективно применять ряд Тейлора в теории и на практике для получения точных приближений

Ряд Тейлора является одним из фундаментальных инструментов математического анализа, широко используемым для приближенного вычисления значений функций. В этой подборке мы собрали полезные советы и примеры использования этого мощного метода в различных областях науки и техники.

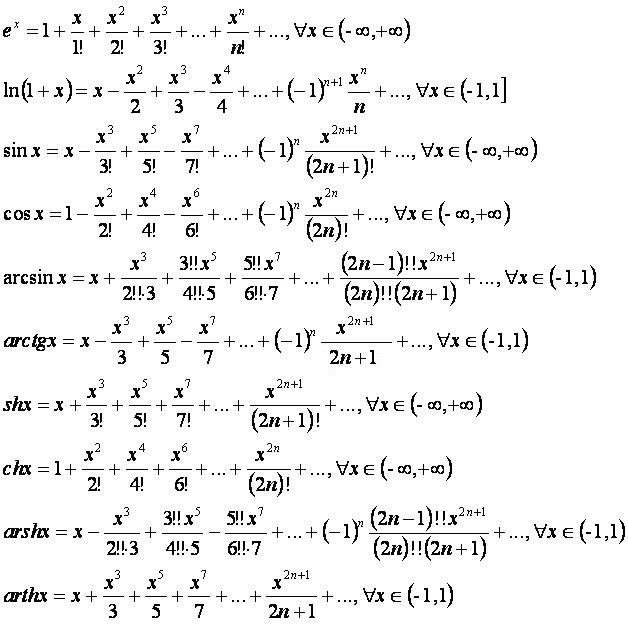
Прежде чем использовать ряд Тейлора, убедитесь, что функция, для которой вы ищете приближение, является аналитической в окрестности выбранной точки.

Если функция имеет разрыв или особенности в точке разложения, то применение ряда Тейлора может привести к неверным результатам. В таких случаях лучше использовать другие методы приближения.

Для повышения точности приближений увеличивайте количество членов ряда Тейлора. Чем больше членов, тем точнее будет приближение функции в выбранной точке.

Для вычисления значений функции вблизи точки разложения можно использовать первые несколько членов ряда, но для более удаленных значений потребуется большее количество членов.

Проверьте, что остаточный член ряда (ошибка приближения) стремится к нулю по мере увеличения числа членов ряда. Это обеспечит точность ваших вычислений.

При использовании ряда Тейлора для численных методов важно контролировать погрешности и отслеживать, насколько быстро сходится ряд к истинному значению функции.

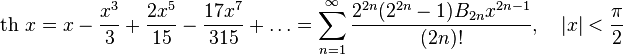
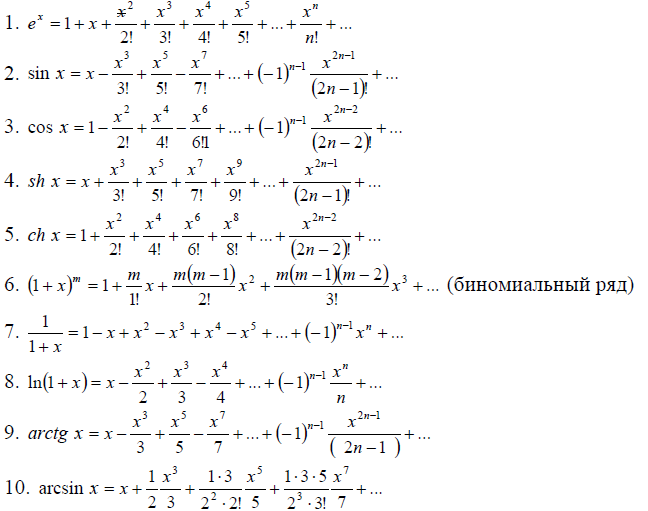
Ряд Тейлора особенно полезен при решении дифференциальных уравнений, когда точное решение сложно найти, а приближенные решения с помощью ряда позволяют получить нужные результаты.

Не забывайте о применении ряда Тейлора для анализа локальных свойств функции, таких как экстремумы и точки перегиба, что может быть полезно в различных областях физики и инженерии.

При работе с многочленами старайтесь сокращать количество членов ряда, чтобы облегчить дальнейшие вычисления, сохраняя необходимую точность приближения.

Используйте графическое представление ряда Тейлора для наглядной оценки качества приближения функции и определения зоны хорошей сходимости.