Как эффективно строить и настраивать параметрические кривые для решения сложных задач
В этом разделе мы рассмотрим основы построения параметрических кривых, их роль в различных областях, а также полезные советы для оптимизации этих процессов. Параметрические кривые играют ключевую роль в математическом моделировании, инженерии, дизайне и других сферах, где важно точно задавать форму объекта с помощью параметров.
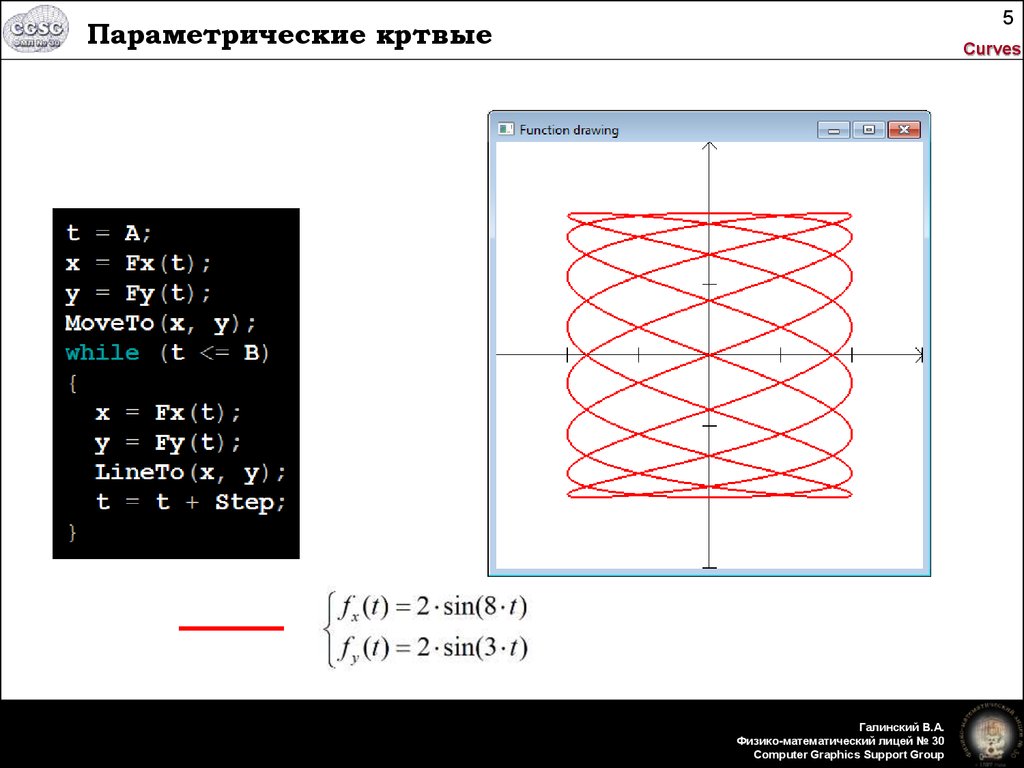
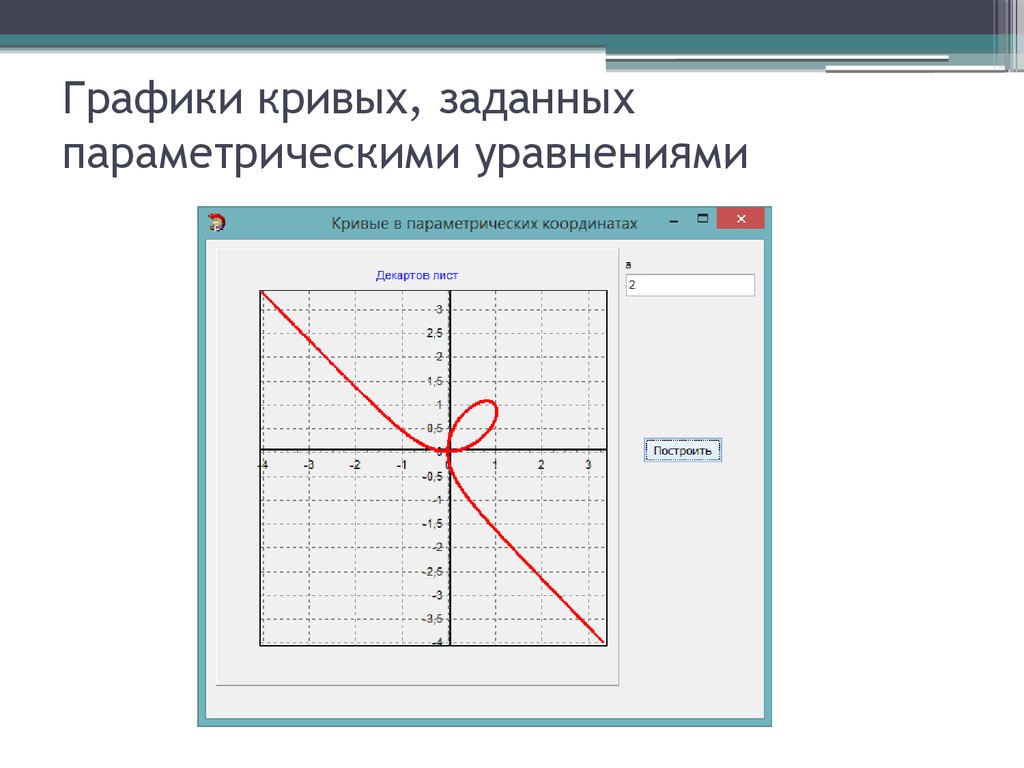

При построении параметрической кривой важно правильно выбрать начальные условия, чтобы избежать нежелательных деформаций в процессе моделирования.

Видеосправочник МК. Построение кривой, заданной параметрически

Для достижения точности всегда проверяйте результаты построения кривых на различных промежуточных шагах, чтобы избежать ошибок в расчетах.

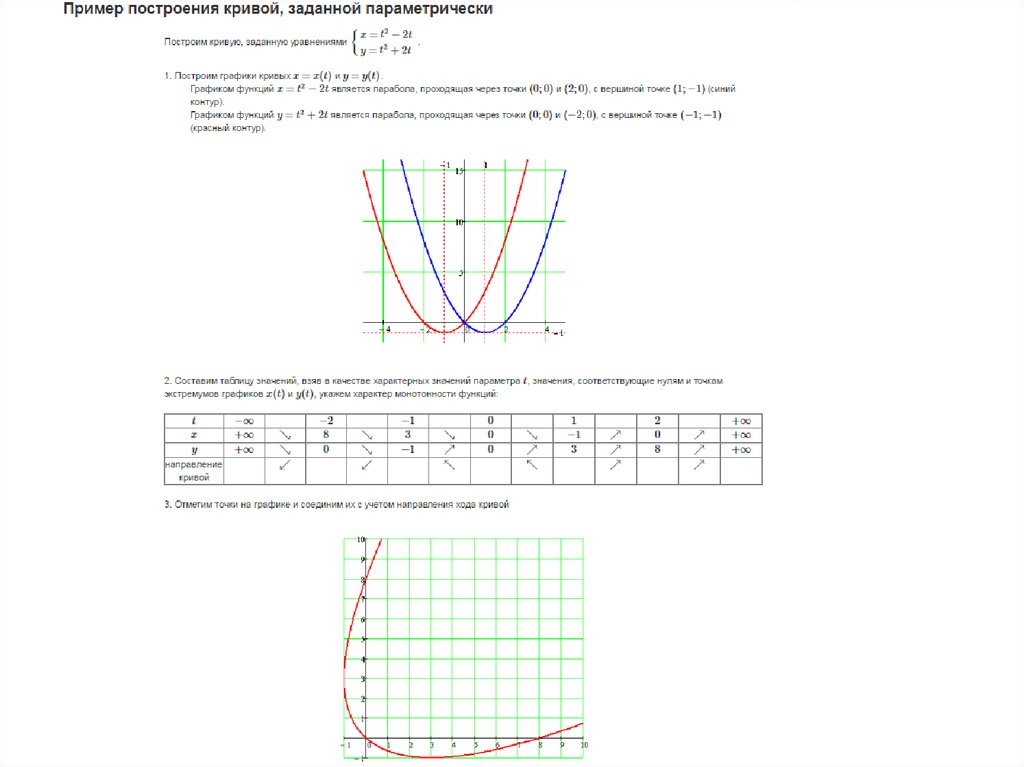
Как построить кривую, заданную параметрически
Используйте инструменты для визуализации кривых, чтобы легче понимать их поведение и вносить корректировки при необходимости.

Построить образ кривой заданной в параметрическом виде

Параметрические кривые могут быть сложными, поэтому рекомендуется разбивать задачу на несколько этапов для упрощения процесса.
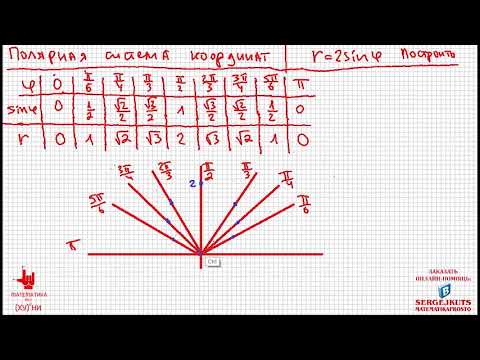
Математика Без Ху%!ни. Полярные координаты. Построение графика функции.
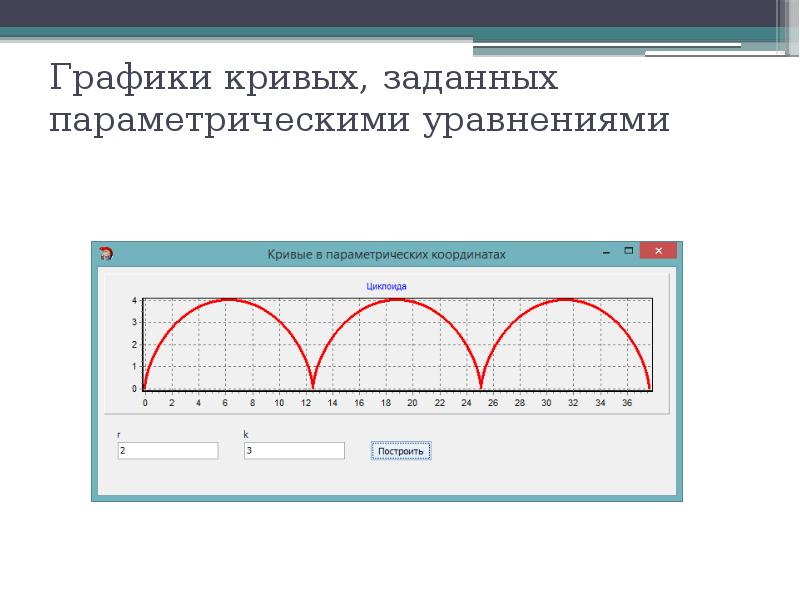
Не забывайте о том, что изменения в одном параметре могут существенно повлиять на все остальные характеристики кривой, учитывайте это при настройке.

Построение кривой в полярной системе координат


Оптимизируйте параметры кривых для улучшения их точности, особенно если они используются для сложных вычислений или моделирования.
Работая с параметрическими кривыми, следите за их гладкостью, чтобы избежать резких переходов и зазоров, которые могут негативно повлиять на результат.
Проверяйте устойчивость параметрических кривых на разных уровнях, чтобы убедиться в их правильной интерпретации и использовании в проекте.

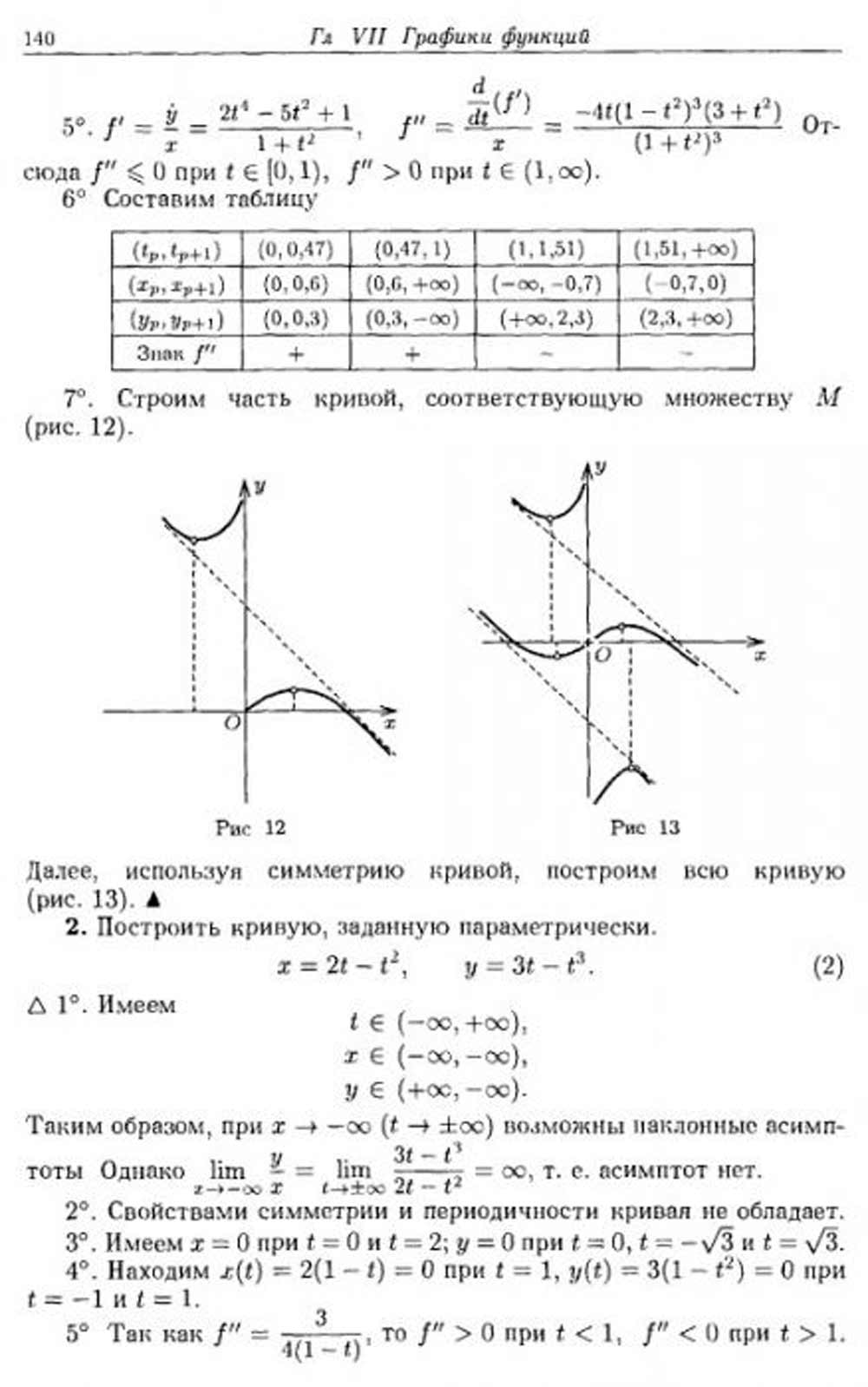
14. Что такое параметрически заданная функция, производная параметрически заданной функции.

Кривые, заданные параметрически
Сохраняйте результаты на каждом этапе работы с параметрической кривой, чтобы в случае ошибки можно было вернуться к предыдущим значениям.

20.12.2021 Практика 26. Построение графиков функций, заданных параметрически
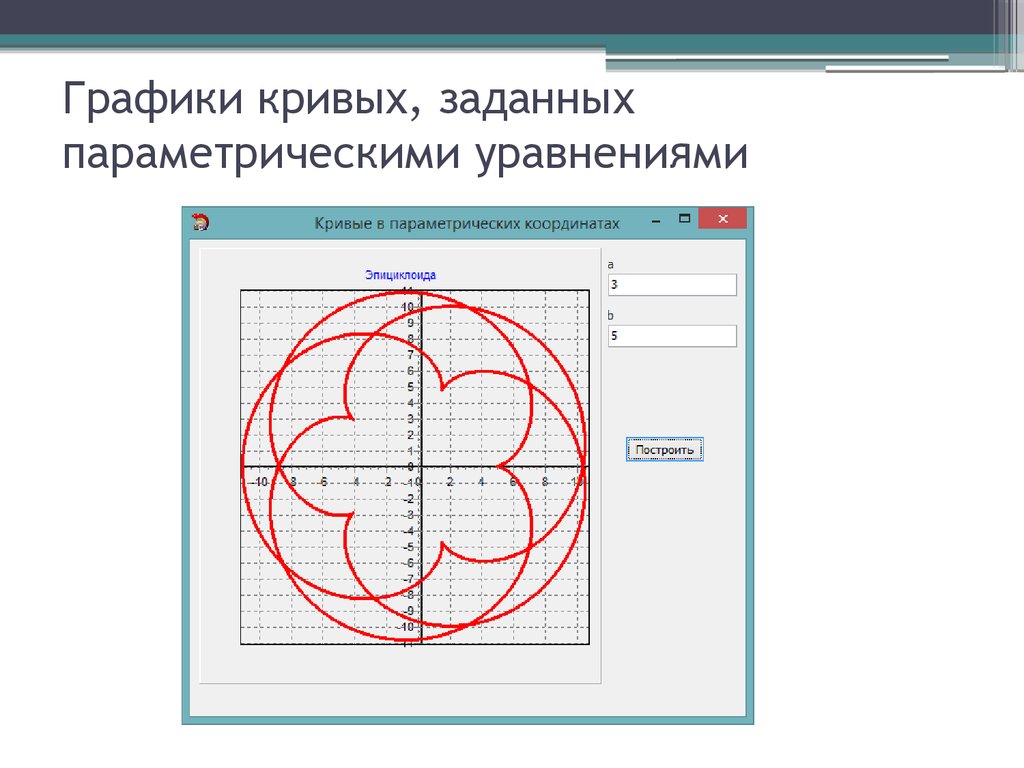

Использование различных типов параметрических кривых, таких как сплайны или кривые Безье, может значительно облегчить задачу моделирования сложных форм.

Математический анализ. ДКР, задание 2. Построение графика функции, заданной параметрически
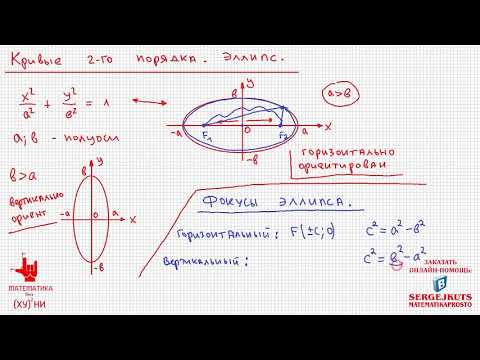
Математика без Ху%!ни. Кривые второго порядка. Эллипс.