Геометрический смысл полного дифференциала функции и его практическое применение
Полный дифференциал функции является важным понятием в математике, особенно в анализе многомерных функций. Он позволяет приблизительно оценить изменение функции при малых изменениях её аргументов. В этом разделе мы рассмотрим геометрический смысл полного дифференциала, его связь с производными и способы использования в различных областях математики и физики.

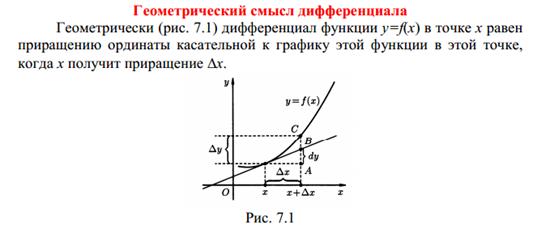
Для понимания геометрического смысла полного дифференциала важно представить, как небольшие изменения входных переменных влияют на результат функции.

22. Дифференциал функции и его геометрический смысл
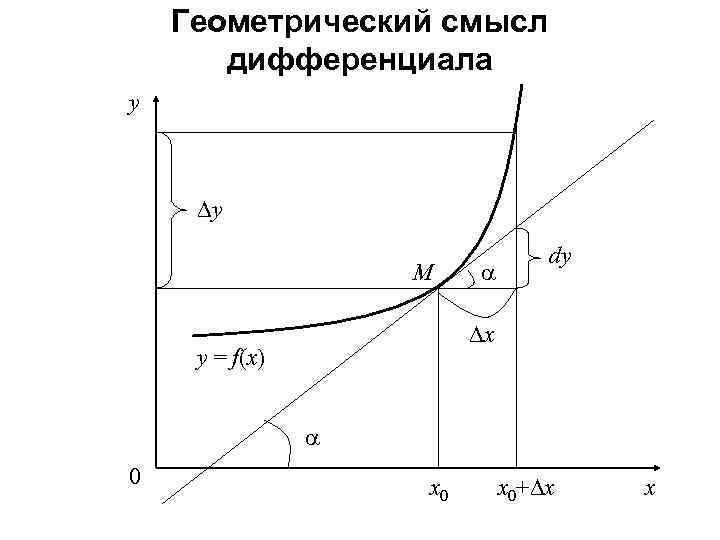
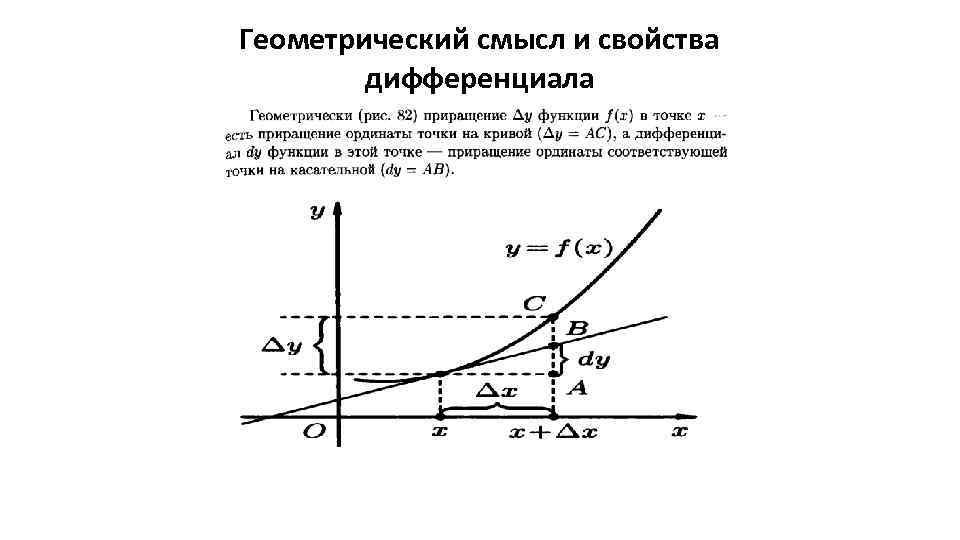
Используйте полные дифференциалы для приближенных вычислений, когда нужно оценить изменение функции при малых отклонениях от исходных значений.

Интегралы№1 Понятие Дифференциала Функции
Помните, что полный дифференциал можно использовать для вычисления аппроксимации изменений функции в точке, что особенно полезно в инженерных расчетах.

Производная и дифференциал и их геометрический смысл - 10 - Константин Правдин - ИТМО

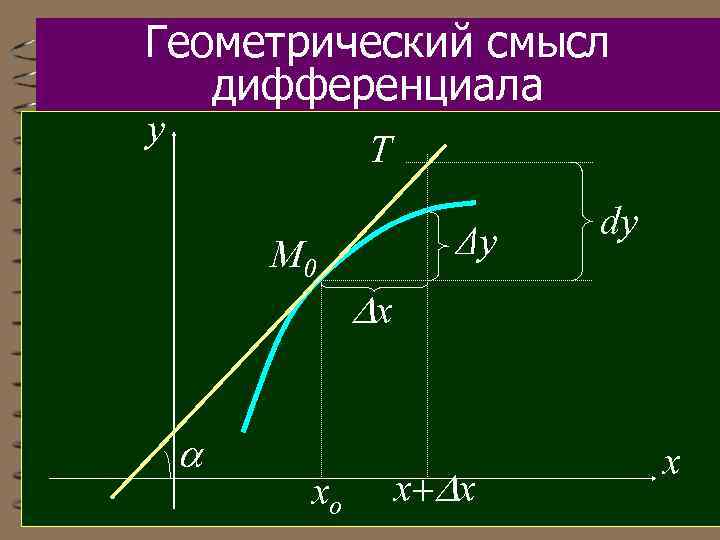
Геометрически полный дифференциал функции можно интерпретировать как касательную плоскость к графику функции в данной точке.

Урок 320. Производная функции и ее геометрический смысл
Для многомерных функций полный дифференциал помогает понять, как изменения всех переменных одновременно влияют на результат.

ПРОИЗВОДНАЯ функции. Объяснение математического смысла.

Практическое применение полного дифференциала важно в физике, особенно в механике и термодинамике, для описания процессов изменения состояния системы.

✓ Касательная. Геометрический смысл производной и дифференциала - матан #033 - Борис Трушин
Вычисляя полный дифференциал, помните о важности точности при выборе малых изменений для аргументов функции.
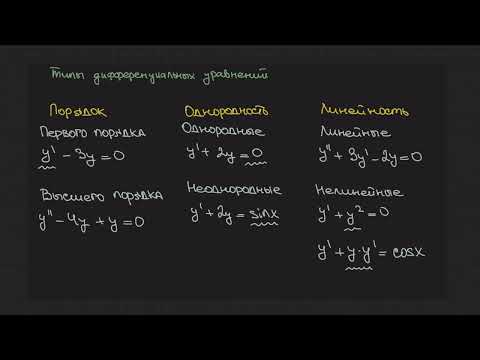
Типы дифференциальных уравнений - Types of Differential Equations
Используйте знание полного дифференциала для нахождения погрешностей в численных методах и для более точных приближений в задачах оптимизации.
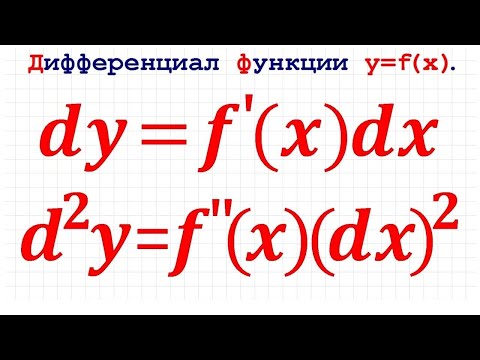
Дифференциал функции

Обратите внимание на связь между частными производными и полным дифференциалом, что помогает понять, как изменения отдельных переменных сказываются на функции в целом.
Дифференциал функции

Полный дифференциал можно использовать для анализа зависимости величин в сложных математических моделях, где функция зависит от нескольких переменных.


✓ Дифференцируемая функция. Дифференциал - матан #032 - Борис Трушин