Все, что нужно знать о периодичности функции косинуса и её графике
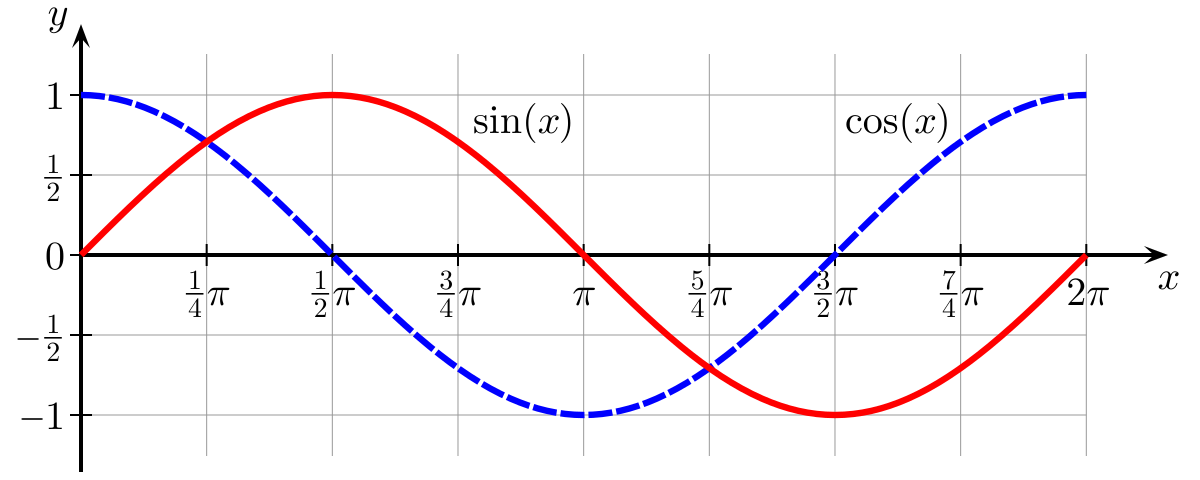
График функции косинуса представляет собой периодическую кривую, которая повторяется через определённые промежутки времени. Понимание периода косинусной функции важно для анализа колебаний, волн и других математических явлений. В этой статье мы расскажем о том, что такое период графика косинуса, как его определить и применить на практике в различных областях, от физики до инженерии.

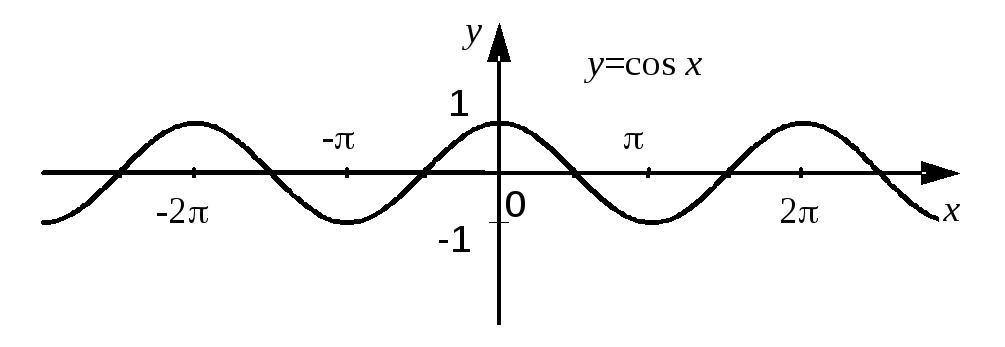
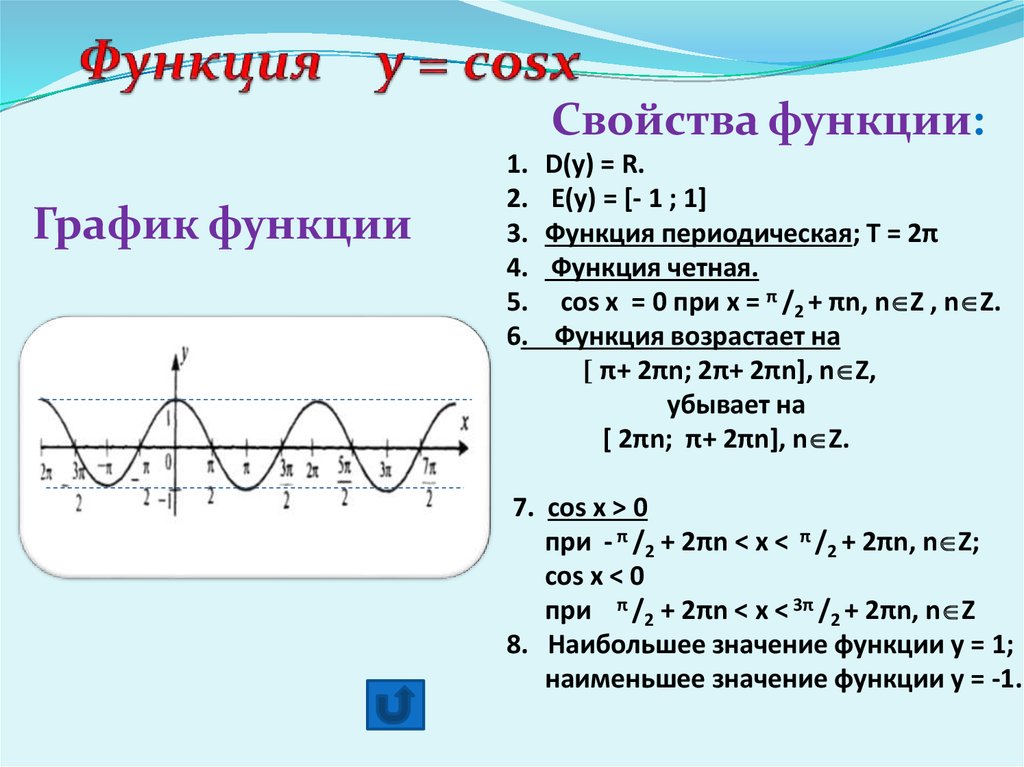
Чтобы вычислить период функции косинуса, нужно помнить, что его стандартное значение для косинуса — 2π.

Построение графиков тригонометрических функций с помощью преобразований. Практ. часть. 10 класс.

Не забывайте, что изменение коэффициентов в аргументе косинуса, например, 2x вместо x, сокращает период функции, делая его равным π.
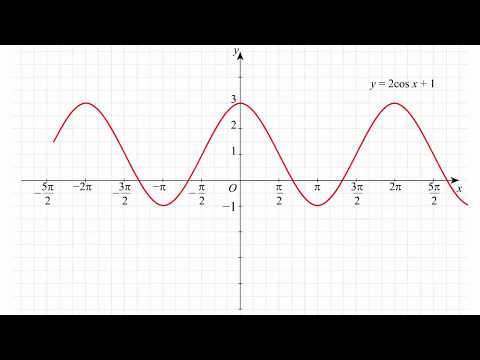
Построение графика функции y=2cos(x)+1
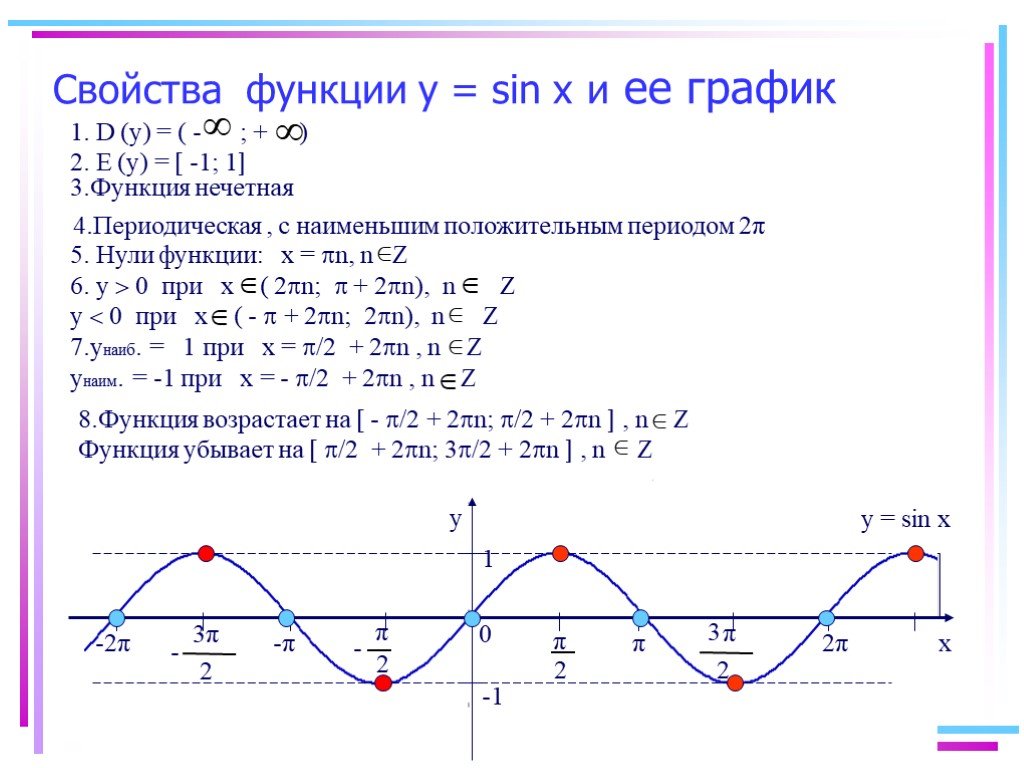

Для нахождения точных значений графика функции косинуса полезно использовать калькуляторы или графические программы, чтобы увидеть, как изменяется его форма в зависимости от коэффициентов.
Тригонометрическая функция, y=cosx и ее свойства. 10 класс.
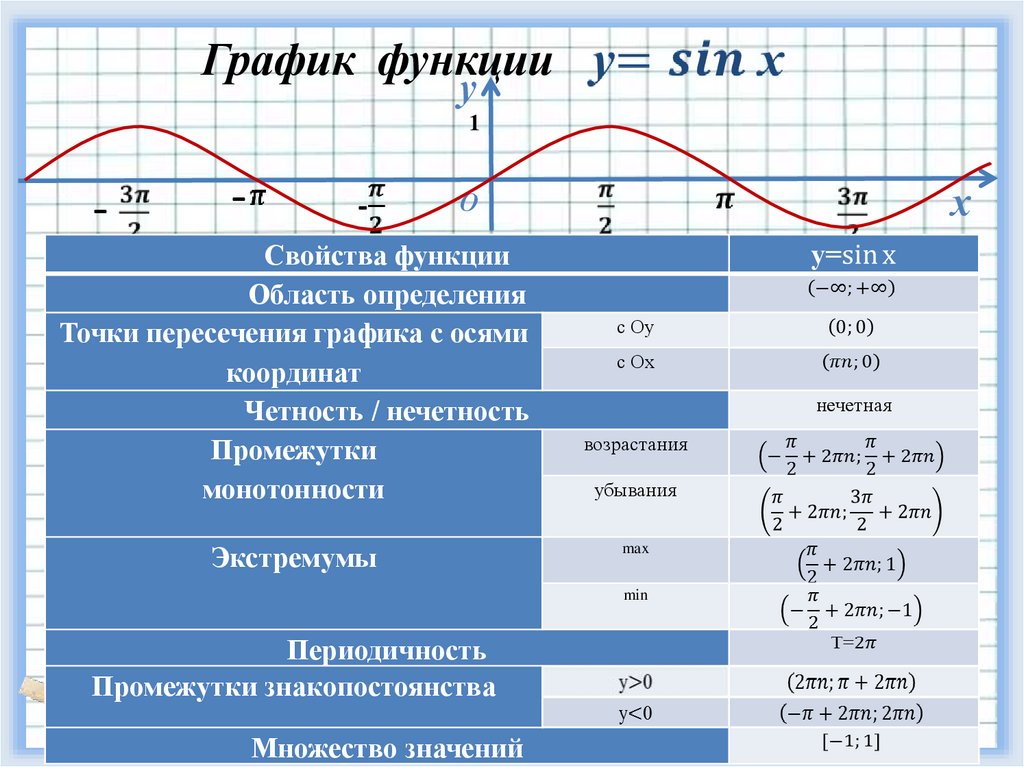

Помимо теории, практическое применение периодичности косинуса встречается в моделировании звуковых волн и колебаний в инженерии.
График функции y=sinx и ее свойства. 10 класс.

При анализе графика косинуса важно учитывать амплитуду функции, которая может изменяться в зависимости от коэффициентов перед косинусом.

Свойства функции. Периодичность. 10 класс.
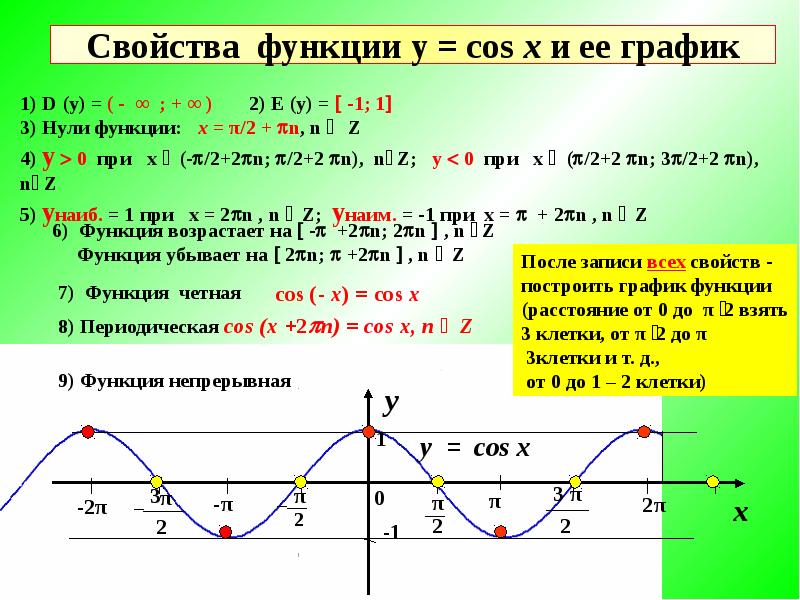
Для более глубокого понимания, рассмотрите взаимосвязь между функцией косинуса и синусоидальными сигналами, которые также обладают периодической природой.
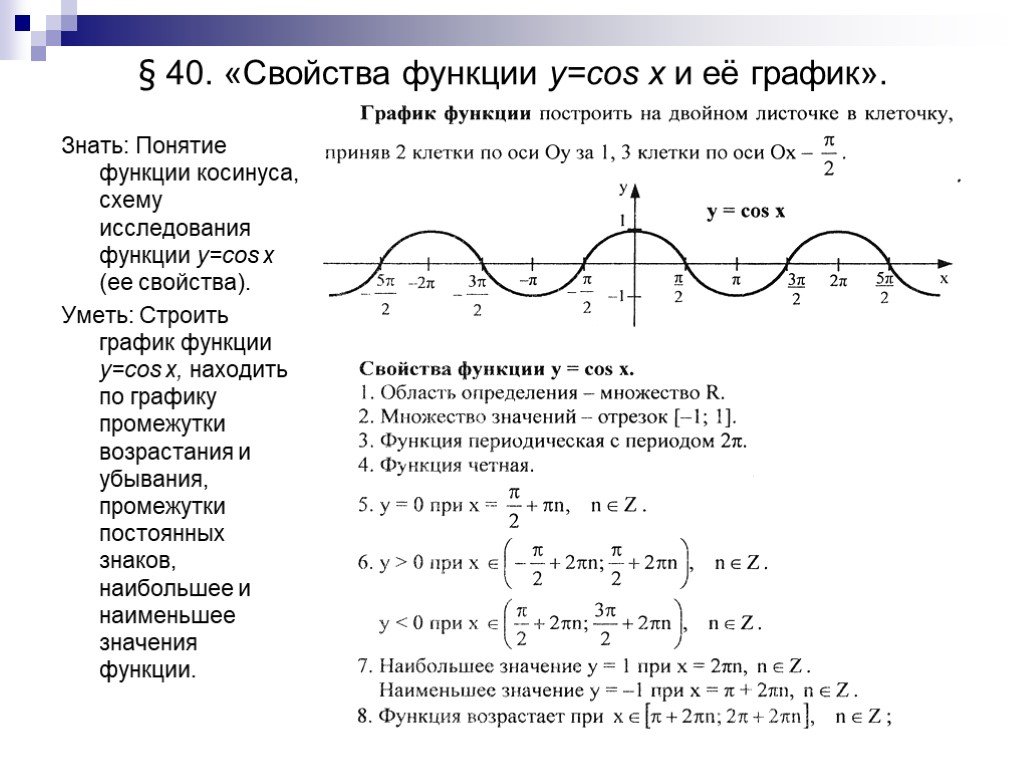
Чтобы ускорить анализ графиков, используйте современные инструменты визуализации данных, такие как Matplotlib в Python, для построения точных графиков.
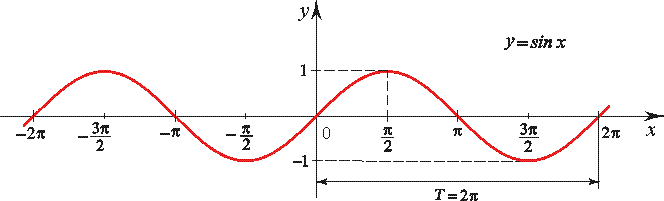

Если необходимо найти период сложной функции, включающей косинус, определите минимальное расстояние между точками, где функция повторяет своё значение.
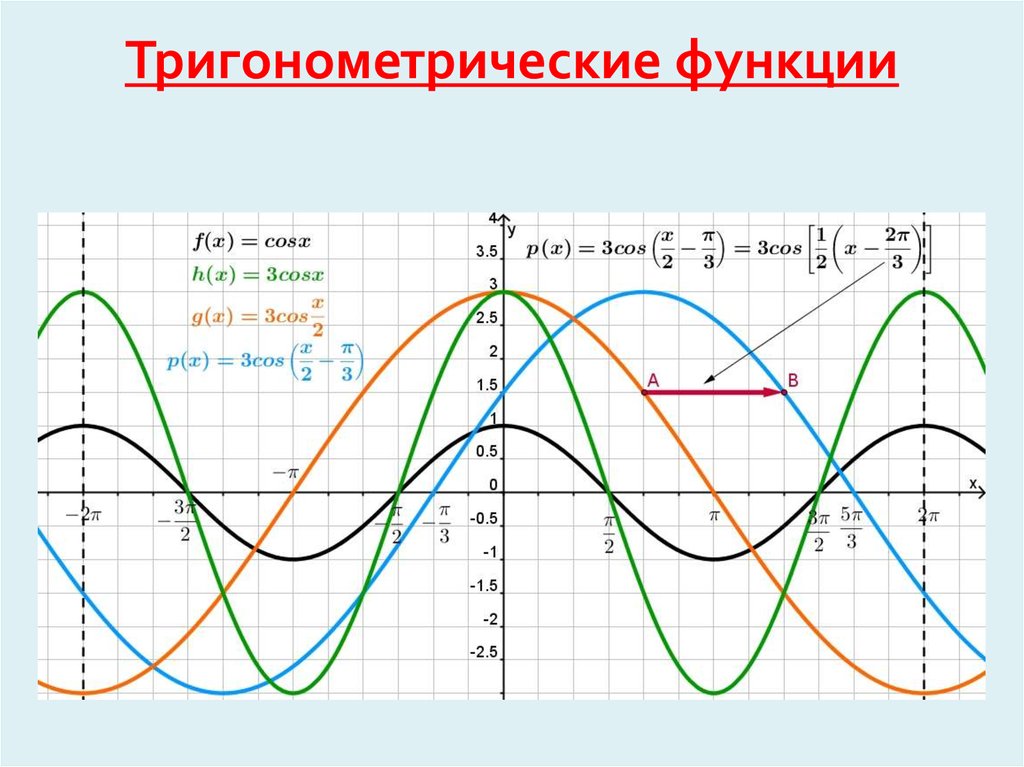
Внимание к деталям, таким как сдвиг фазы или изменения амплитуды, поможет вам лучше понимать, как изменяется график косинуса в реальных приложениях.
Не забывайте, что точность вычислений и корректная интерпретация графика играют ключевую роль в решении задач, связанных с периодическими функциями.