Принцип, по которому отрезок равен сумме частей: важные советы и пояснения

На этой странице собраны полезные советы и примеры, которые помогут разобраться, как отрезок может быть равен сумме своих частей. Мы рассмотрим практическое применение этого принципа и дадим рекомендации для решения задач в геометрии и других областях.

При делении отрезка на несколько частей важно помнить, что его длина будет равна сумме длин этих частей, если они соединены без промежутков.

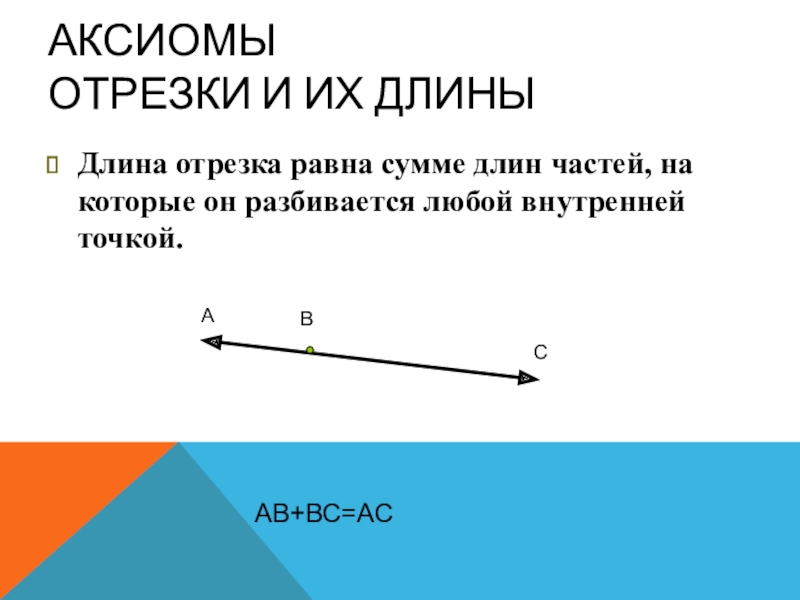
Этот принцип можно использовать для проверки правильности решений в задачах на нахождение длины отрезков в геометрии.

Для удобства представления отрезка, разделенного на части, можно использовать визуальные схемы, чтобы наглядно увидеть, что сумма частей всегда равна целому отрезку.

Обратите внимание, что если части отрезка равны между собой, это может упростить задачу, так как вам нужно будет лишь умножить длину одной части на количество частей.

Когда несколько отрезков составляют один, важно не только сложить их длины, но и убедиться, что они лежат на одной прямой или правильно соединены.

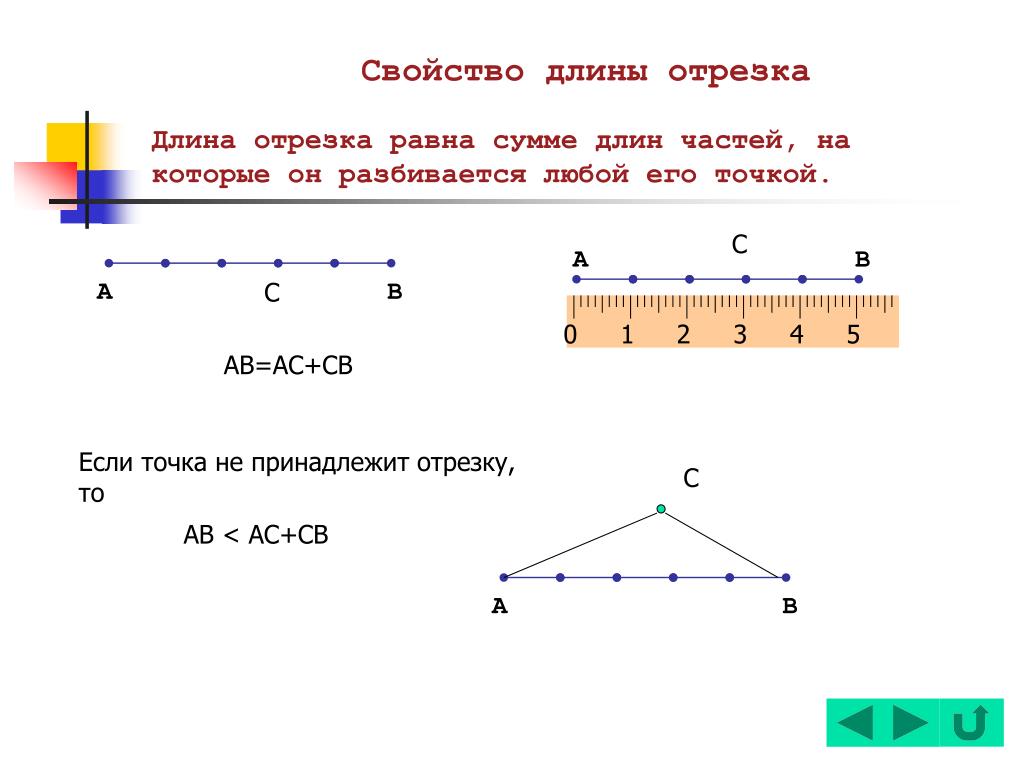
Для решения более сложных задач на отрезки можно использовать этот принцип в сочетании с другими геометрическими правилами, например, для нахождения длин сторон многоугольников.

Помните, что этот принцип также работает в задачах на равенство длин отрезков, когда требуется доказать, что одна из частей отрезка равна другой.

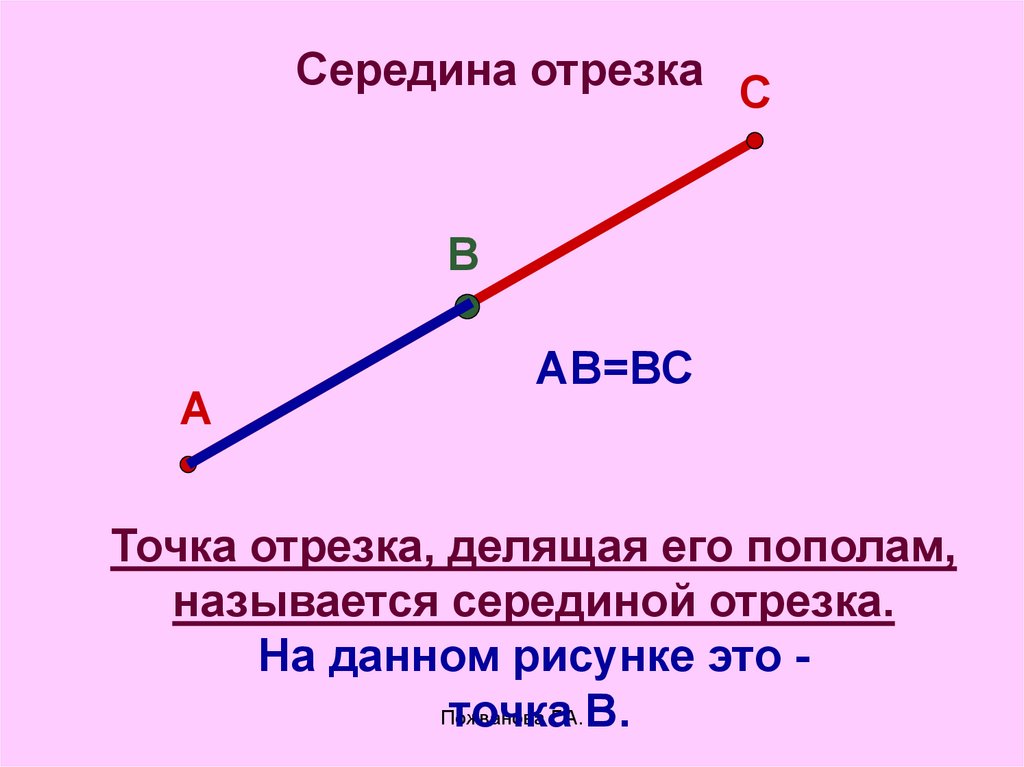
Важно проверять, что каждая из частей отрезка правильно определена, иначе общий результат может быть неточным.

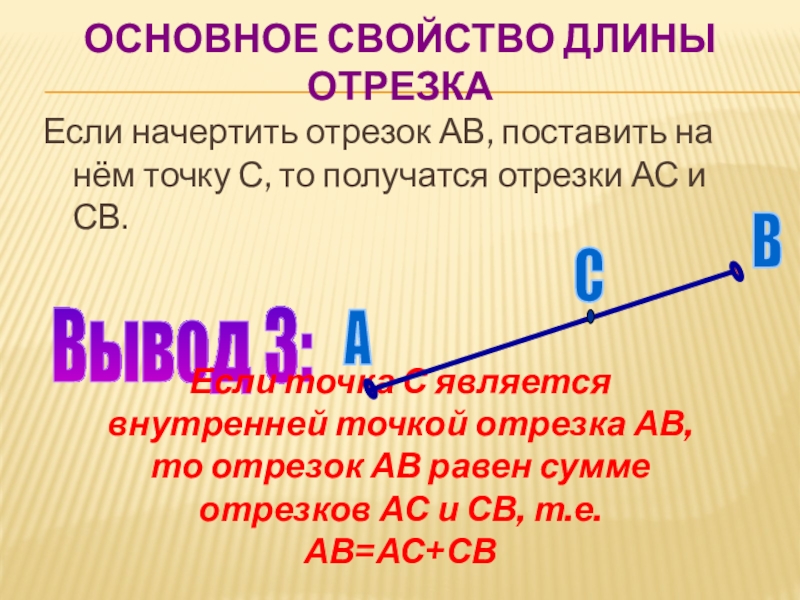
Этот принцип часто используется в расчетах длины диагоналей в различных многоугольниках или сложных геометрических фигурах.

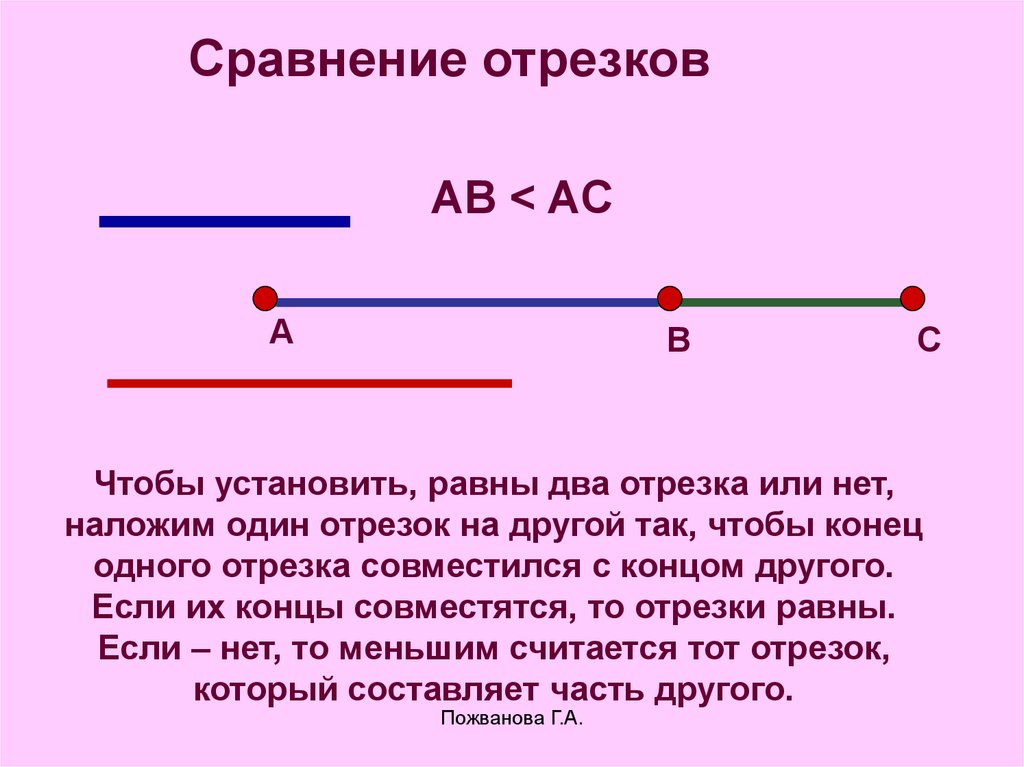
Когда делите отрезок на несколько частей, всегда проверяйте, что их длины соответствуют условиям задачи, чтобы избежать ошибок в расчетах.