Как правильно работать с точками, выбранными на сторонах остроугольного треугольника
На этой странице вы найдете полезные советы и рекомендации, связанные с геометрическими свойствами остроугольных треугольников, в частности, точек, взятых на их сторонах. Разберемся, как эти точки влияют на различные аспекты геометрии и как можно эффективно использовать их для решения задач.

Для эффективного решения задач с точками на сторонах треугольника важно четко понимать их расположение и взаимосвязи между точками.

Особые точки likerkacinema.ruк полюса
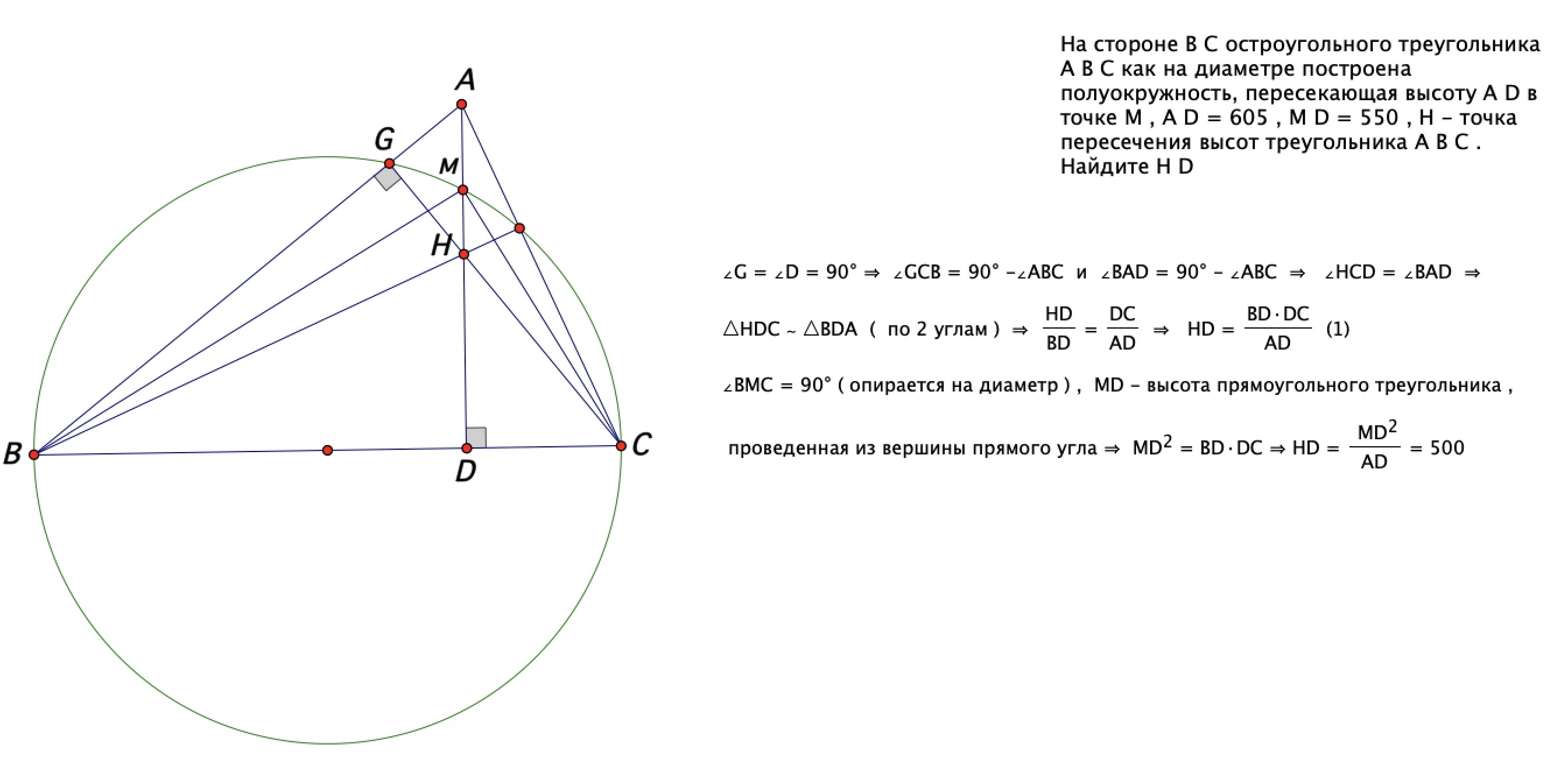
Когда выбираете точку на стороне треугольника, определите ее координаты относительно вершин треугольника для упрощения вычислений.
Остроугольный треугольник
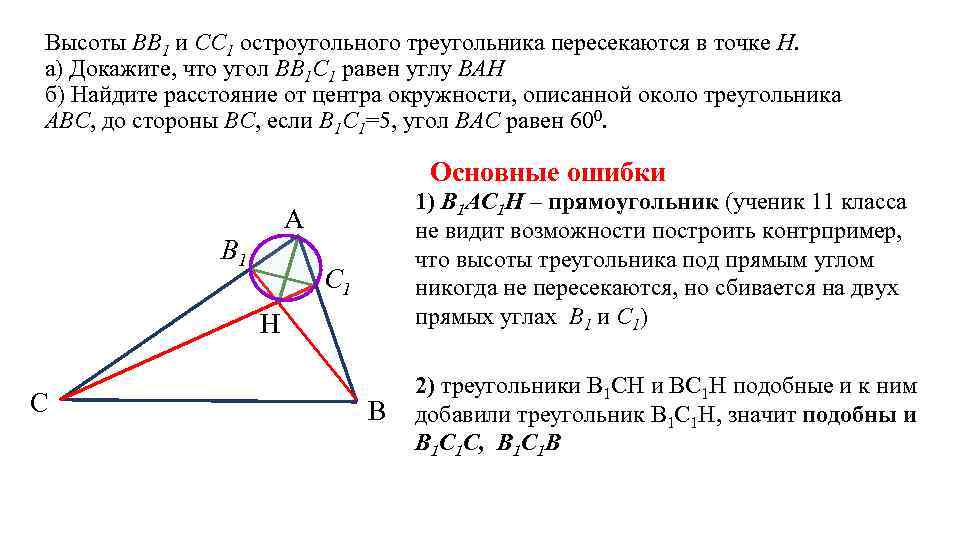
Помимо простых координат, полезно учитывать геометрические отношения, такие как углы и длины отрезков, чтобы лучше понять свойства точек.

Почти никто не решил ➜ Найдите сторону треугольника
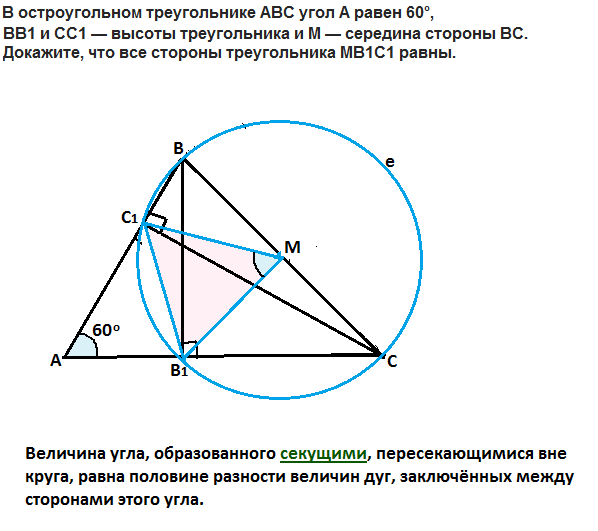
Используйте теорему о пересечении медиан и серединных перпендикуляров для нахождения дополнительных важных точек на сторонах треугольника.
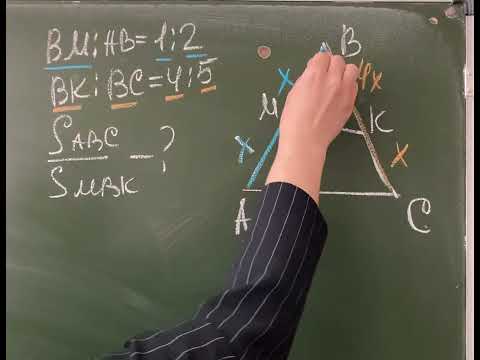
В треугольнике ABC известно на сторонах АВ и ВС отмечены точки М и К
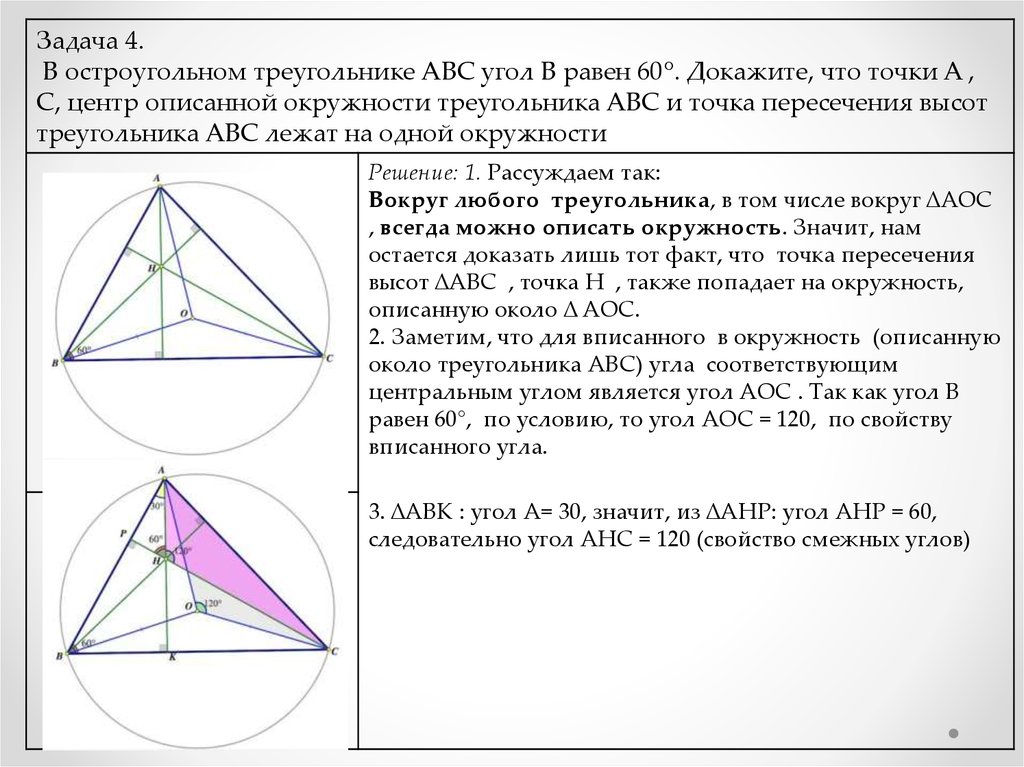
Если на сторонах треугольника выбраны несколько точек, рассмотрите возможность применения теоремы о подобии треугольников для упрощения задач.
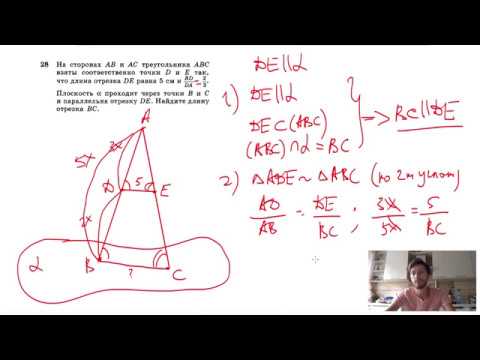
№28. На сторонах АВ и АС треугольника ABC взяты соответственно
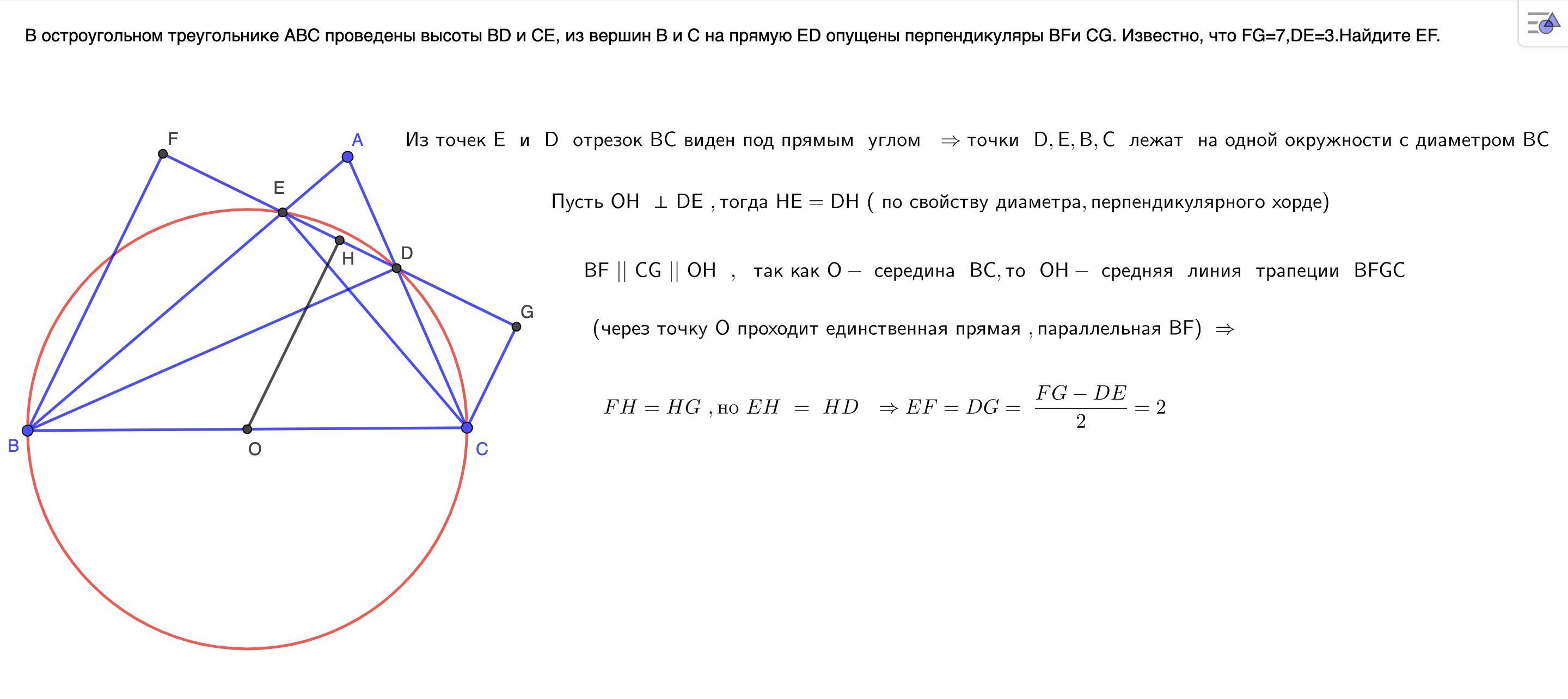
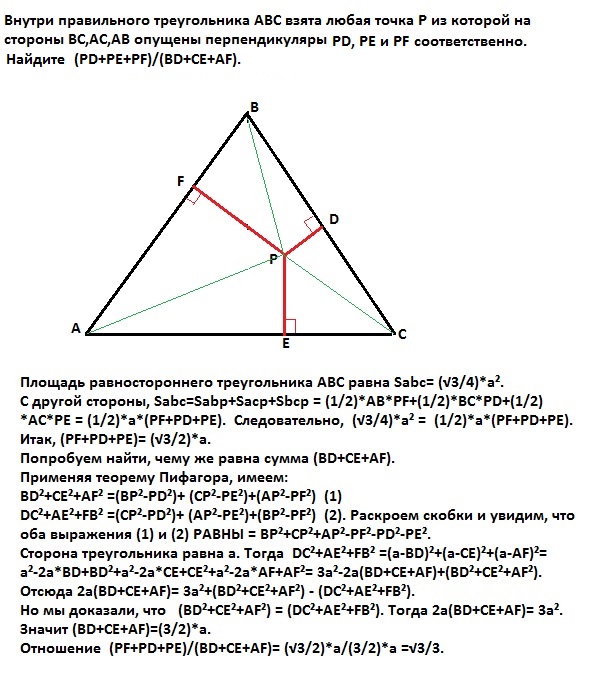
Не забывайте о важности симметрии в геометрии — она может значительно упростить процесс вычислений и построений.

№99. На сторонах угла CAD отмечены точки B и E так, что точка В лежит на отрезке АС, а точка Е —
Использование свойств точек на сторонах треугольника поможет вам решать задачи не только в рамках геометрии, но и в более сложных темах, таких как тригонометрия.

Окружность касается боковых сторон АВ и ВС остроугольного треугольника АВС в точкахА и С соответстве
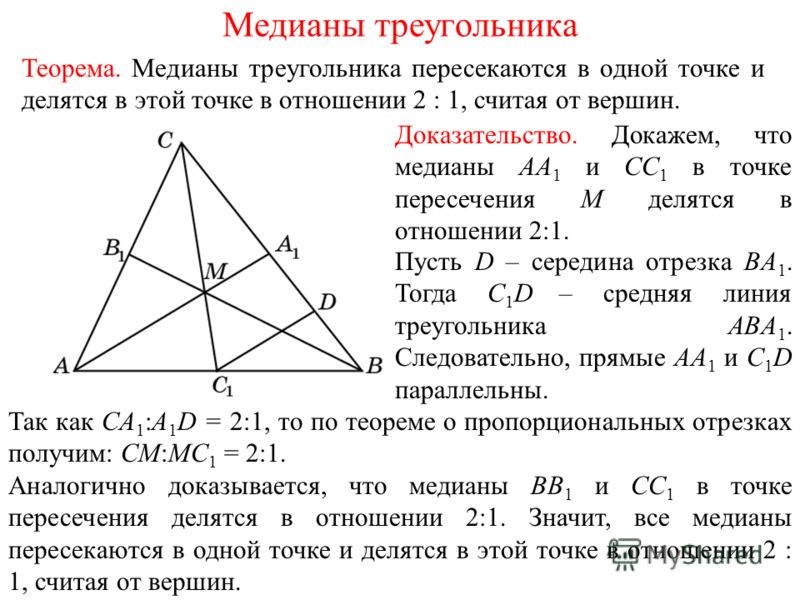
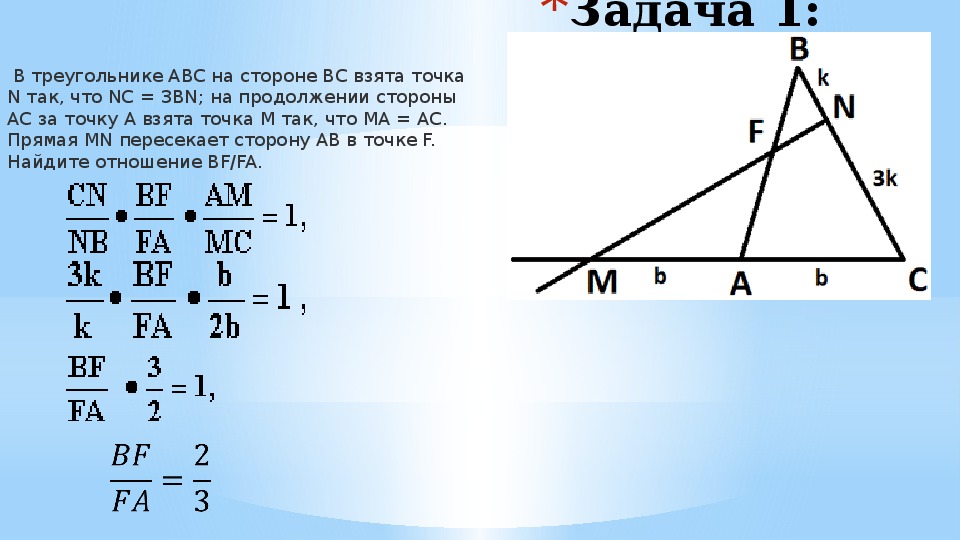
Попробуйте построить несколько разных треугольников с точками на сторонах, чтобы лучше понять, как различные варианты влияют на результаты.
При решении задач с точками на сторонах треугольника полезно использовать различные геометрические инструменты, такие как циркуль и линейка.
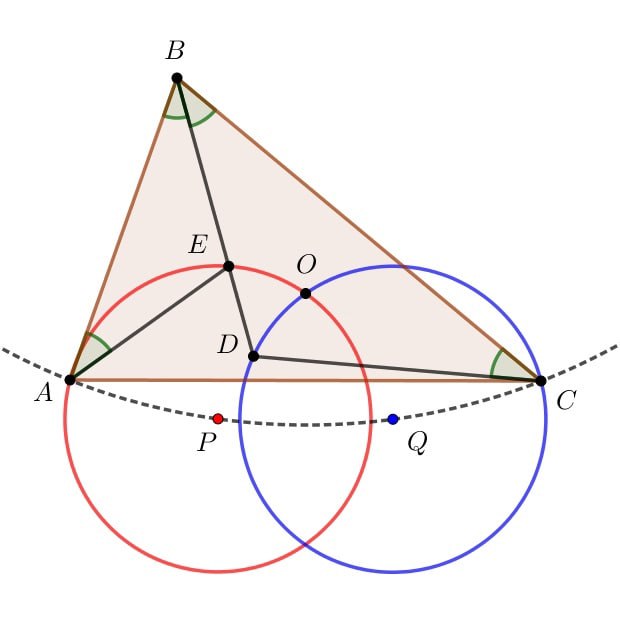
Важно помнить, что каждая точка на стороне треугольника может создавать уникальные условия для решения задачи, поэтому не упускайте из виду все возможные варианты.

ЕГЭ 2023. Конструкции с равнобедренным и прямоугольным треугольником в №№1, 16 ЕГЭ по математике.