Как правильно работать с матрицами: определитель, элементы и основные операции
На этой странице собрана информация о матрицах, их элементах, операциях с матрицами и вычислении определителя. Узнайте, как правильно работать с матрицами, какие существуют основные правила и полезные советы для решения задач. Эти материалы будут полезны как для студентов, так и для всех, кто интересуется математическими методами.
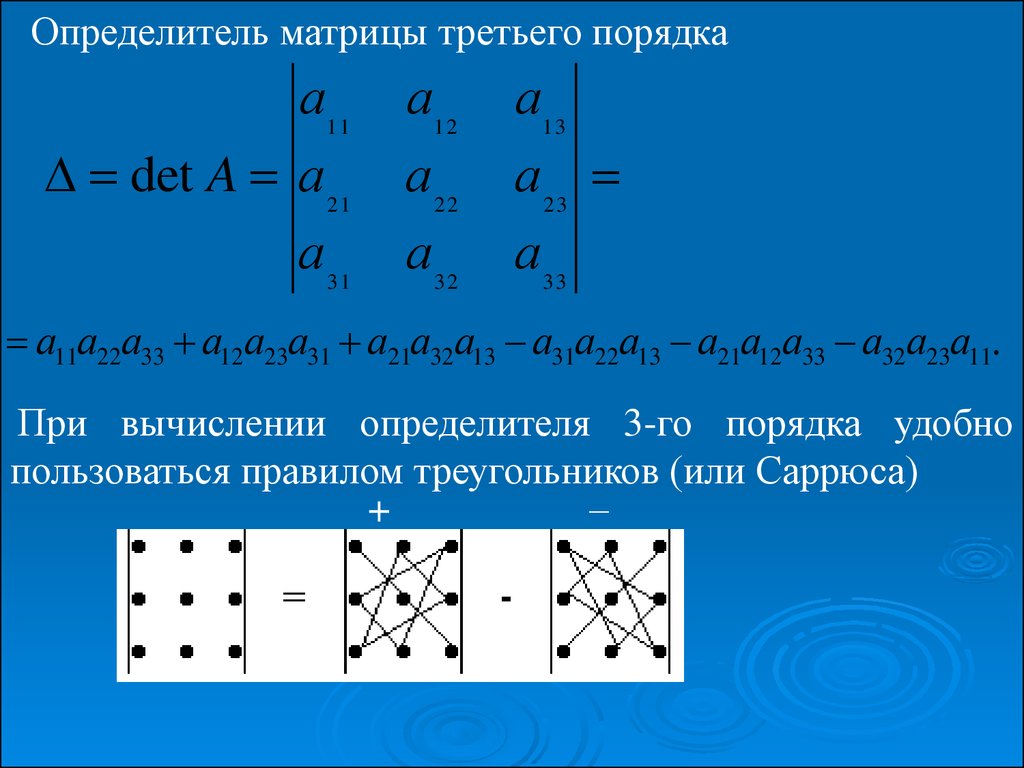

Для начала ознакомьтесь с основами теории матриц: определение, элементы, размерность и типы матриц. Это поможет вам разобраться в дальнейших операциях.

Урок 1. Матрицы, определитель матрицы и ранг матрицы - Высшая математика - TutorOnline


Определитель матрицы помогает оценить свойства матрицы, такие как её обратимость. Если определитель матрицы равен нулю, матрица необратима.

ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 2х2 3х3 4x4 свойства определителя
При вычислении определителя матрицы используйте метод разложения по строкам или столбцам, что позволяет упростить расчёты для больших матриц.

Определитель Матрицы

Помните, что при перемножении матриц размерности должны совпадать: количество столбцов первой матрицы должно равняться количеству строк второй.

Определитель матрицы и все способы его найти

Для вычисления обратной матрицы применяйте метод дополнений и делите на определитель. Если определитель матрицы равен нулю, матрица не имеет обратной.
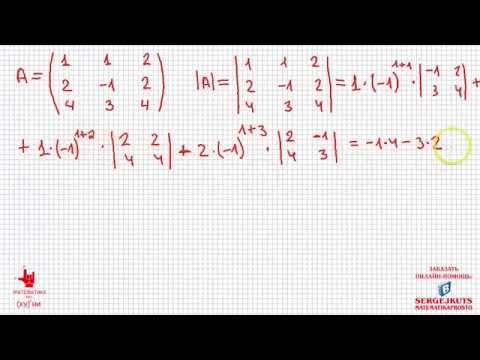
Математика без Ху%!ни. Как вычислить определитель.


Следите за знаками при вычислениях. Неоправданные ошибки со знаками могут сильно повлиять на результат.

Произведение матриц

Работая с большими матрицами, используйте специализированные программы или калькуляторы для упрощения вычислений и ускорения работы.

5 способов вычисления определителя ★ Какой способ лучше?


Для удобства работы с матрицами всегда придерживайтесь строгой нотации и записей: индексирование с использованием строчных и прописных букв, ясное разделение операций.

Матан за час. Шпаргалка для первокурсника. Высшая математика

Как найти определитель матрицы 2х2, 3х3 и 4х4


Изучите различные методы нахождения определителя матрицы, такие как правило Саррюса для матриц 3x3, а также метод миноров и дополнений для более высоких размерностей.

Определитель 5-го порядка


Важно понять геометрическую интерпретацию матриц, особенно для 2x2 и 3x3 матриц, так как это поможет лучше понять их поведение при преобразованиях пространства.