Понимание теоремы Эйлера: важные аспекты и практическое применение в математике

Теорема Эйлера является важным результатом в области математики, находящая широкое применение в различных областях науки и техники. Знание ее принципов помогает решать задачи в теории графов, топологии, теории чисел и многих других дисциплинах. В этой статье вы найдете полезные советы, примеры применения теоремы, а также фотографии, иллюстрирующие ее основные идеи.

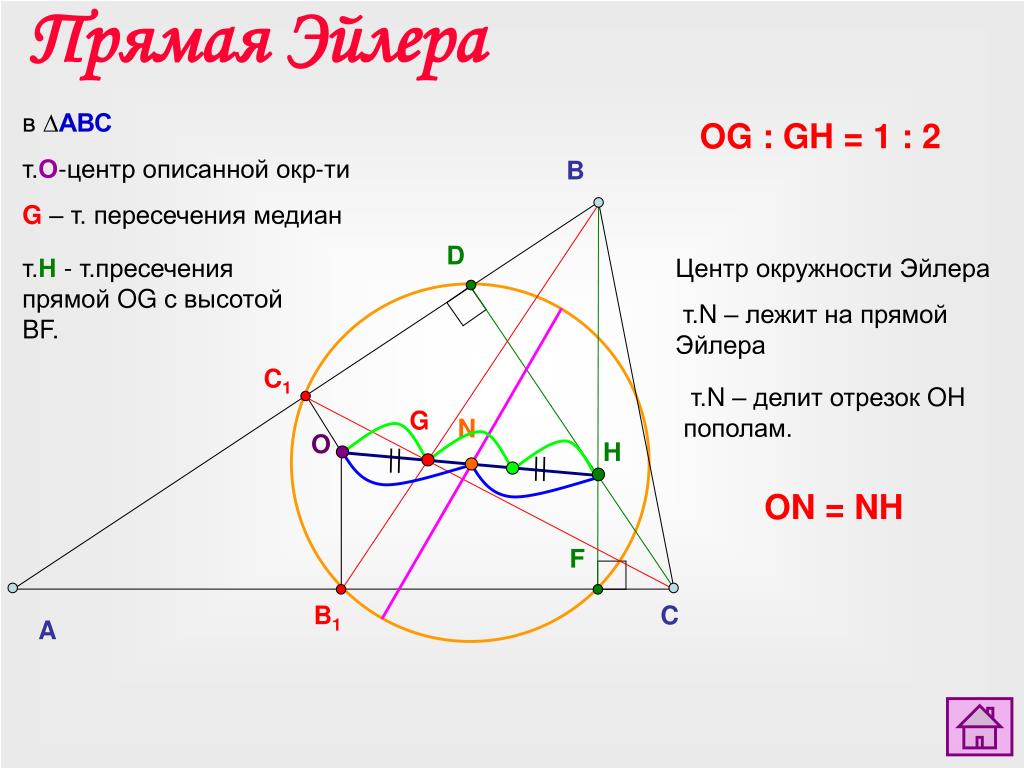
Изучение теоремы Эйлера требует внимательности к деталям и понимания ее основных понятий, таких как графы, вершины и ребра.

Начните с простых примеров и постепенно переходите к более сложным, чтобы лучше освоить теорему Эйлера и ее применение.

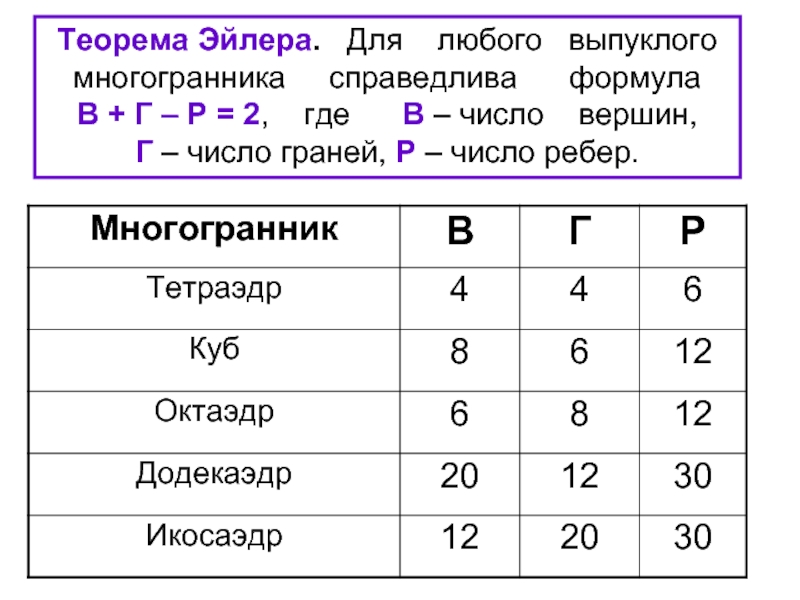
Для лучшего понимания теоремы полезно визуализировать графы и их свойства с помощью различных программных средств.

Теорема Эйлера активно используется в решении задач о кратчайших путях, оптимизации и планировании, поэтому стоит изучать ее применение в этих областях.

Не забывайте о математической индукции при доказательствах, так как это важный инструмент для подтверждения теоремы Эйлера.

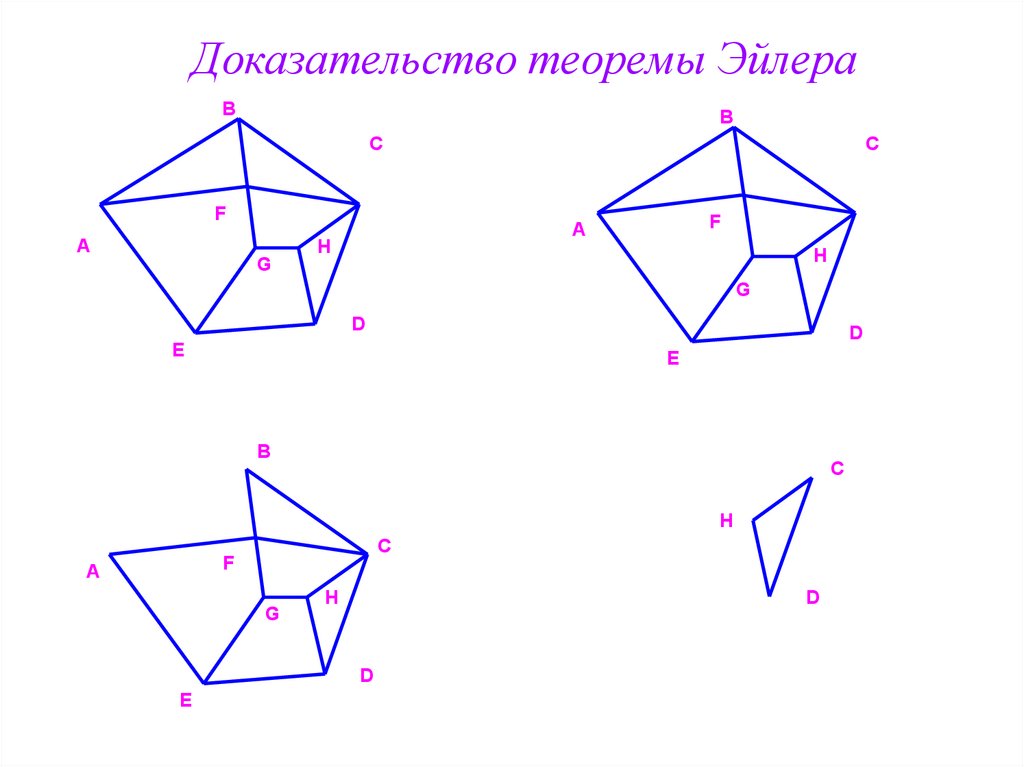
Чтение научных работ и статей по теореме Эйлера может существенно углубить ваше понимание и расширить кругозор.

Постарайтесь применять теорему Эйлера не только в теории, но и в реальных ситуациях, например, в задачах по логистике или в компьютерных сетях.

Обратите внимание на связь теоремы Эйлера с другими математическими концепциями, такими как теорема о мостах Кенига.

Не бойтесь ошибаться в расчетах на первых этапах изучения теоремы — это естественная часть процесса обучения.

Регулярно решайте задачи, связанные с теоремой Эйлера, чтобы закрепить полученные знания и повысить свою уверенность в математике.