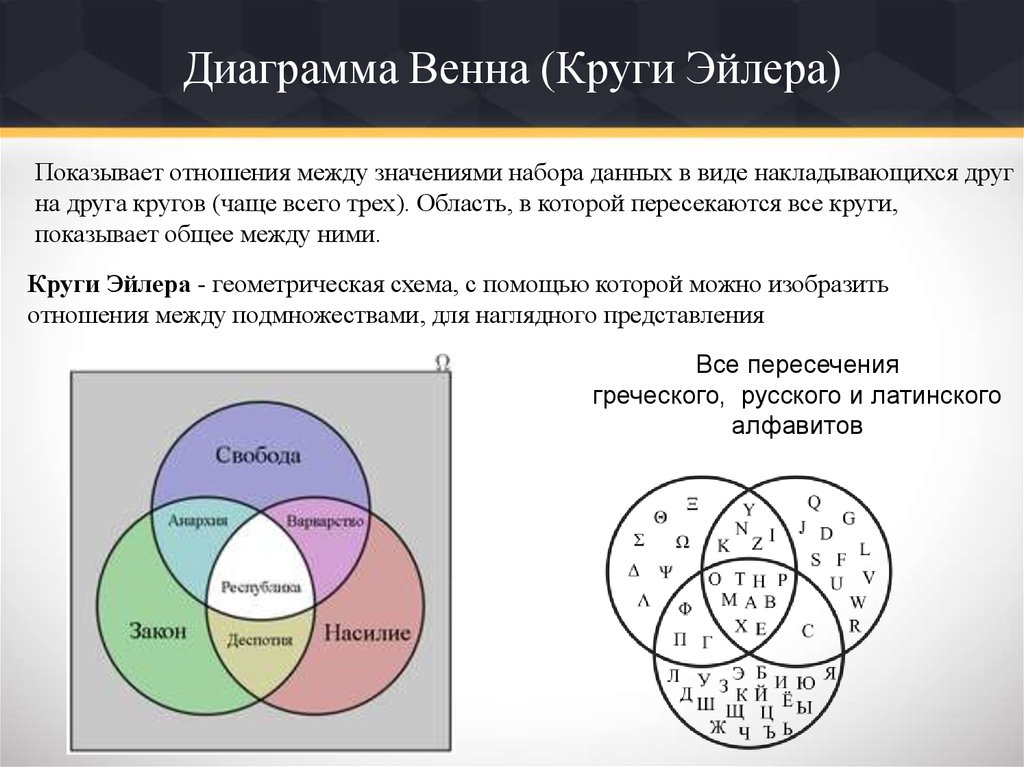
Отрицание в кругах Эйлера и Венна: понятный разбор
Круги Эйлера и Венна — мощный инструмент для визуализации логических операций, таких как отрицание. На этой странице вы найдете подборку фотографий, схем и полезные советы для изучения и применения этой темы.
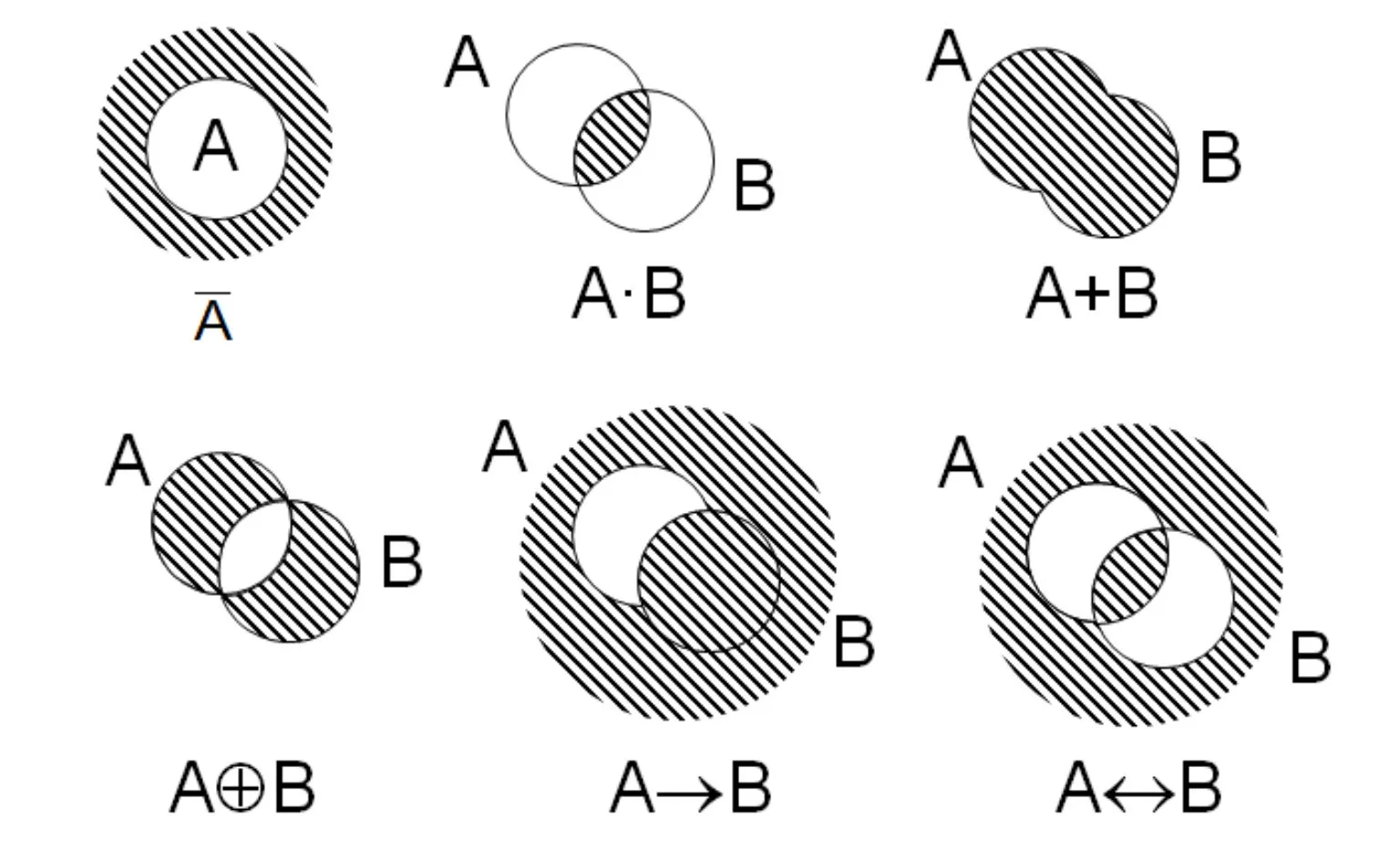

Начните с простых схем: создайте круги для представления двух множеств и обозначьте их пересечения, чтобы лучше понять базовые принципы.

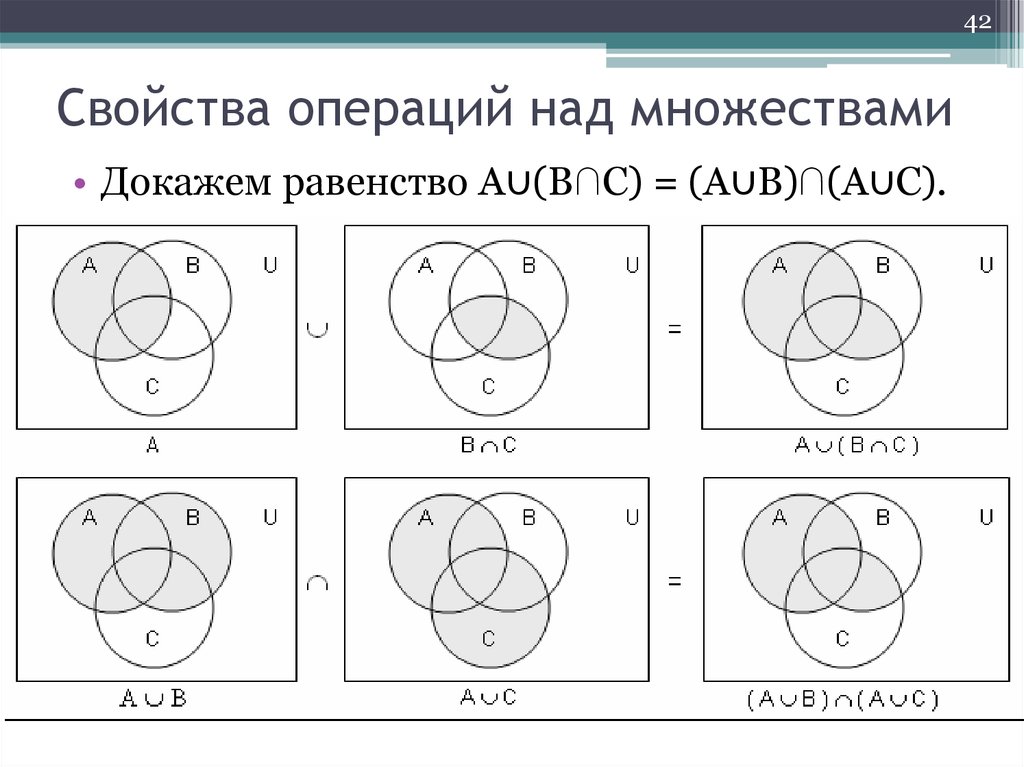
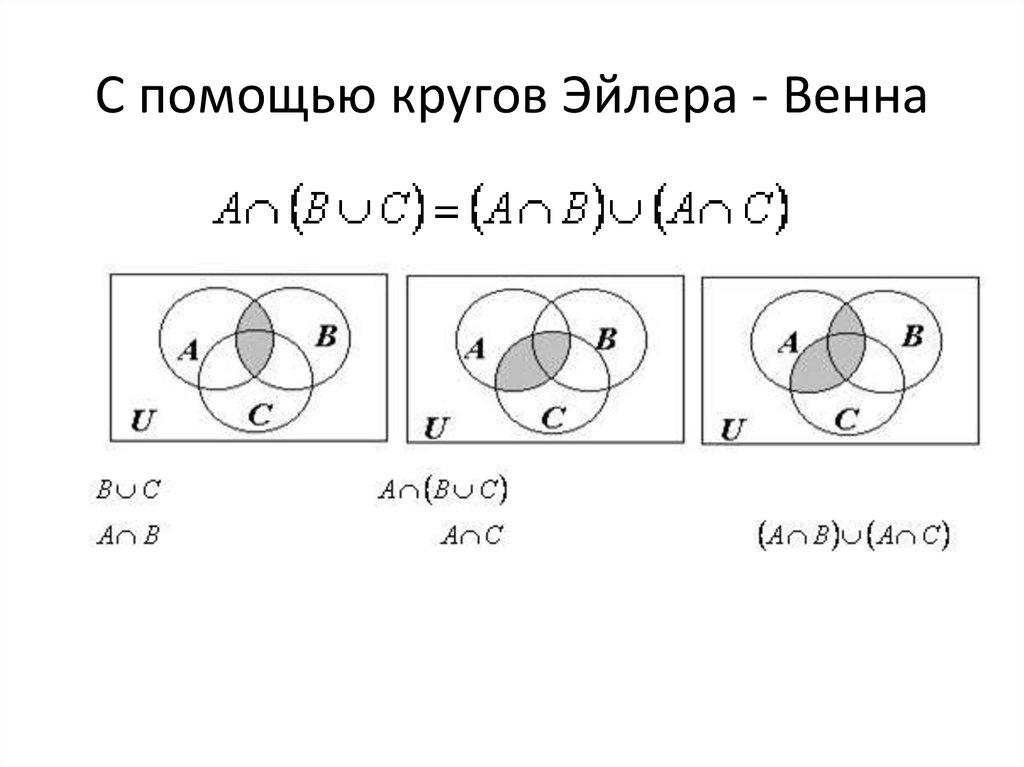
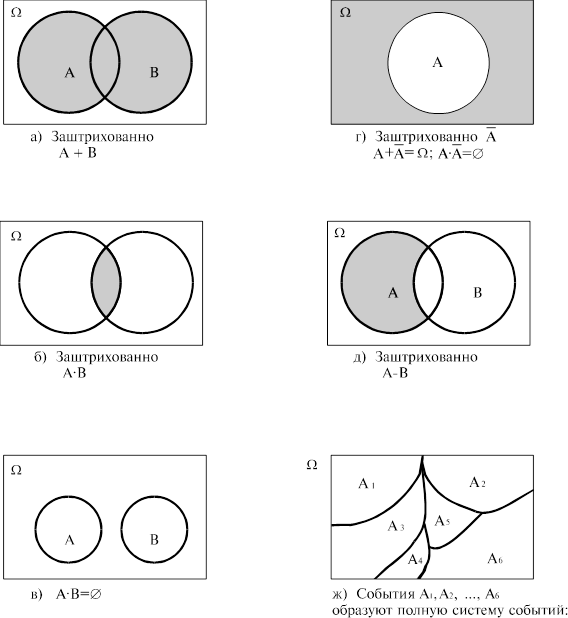
Доказать равенства при помощи диаграмм Эйлера-Венна. Действия над множествами.

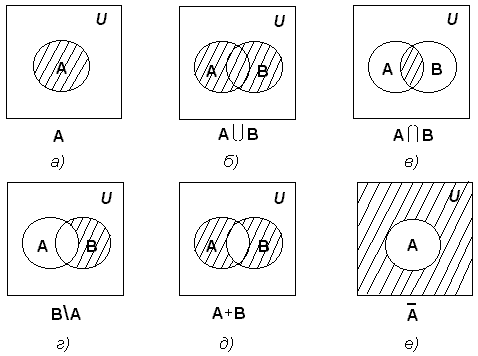
Для изучения отрицания отметьте область вне заданного множества, чтобы увидеть, что остается за его пределами.

Разбор ОГЭ по информатике на 5. Разбор второй части ОГЭ на Linux - Информатика ОГЭ 2024 - Умскул
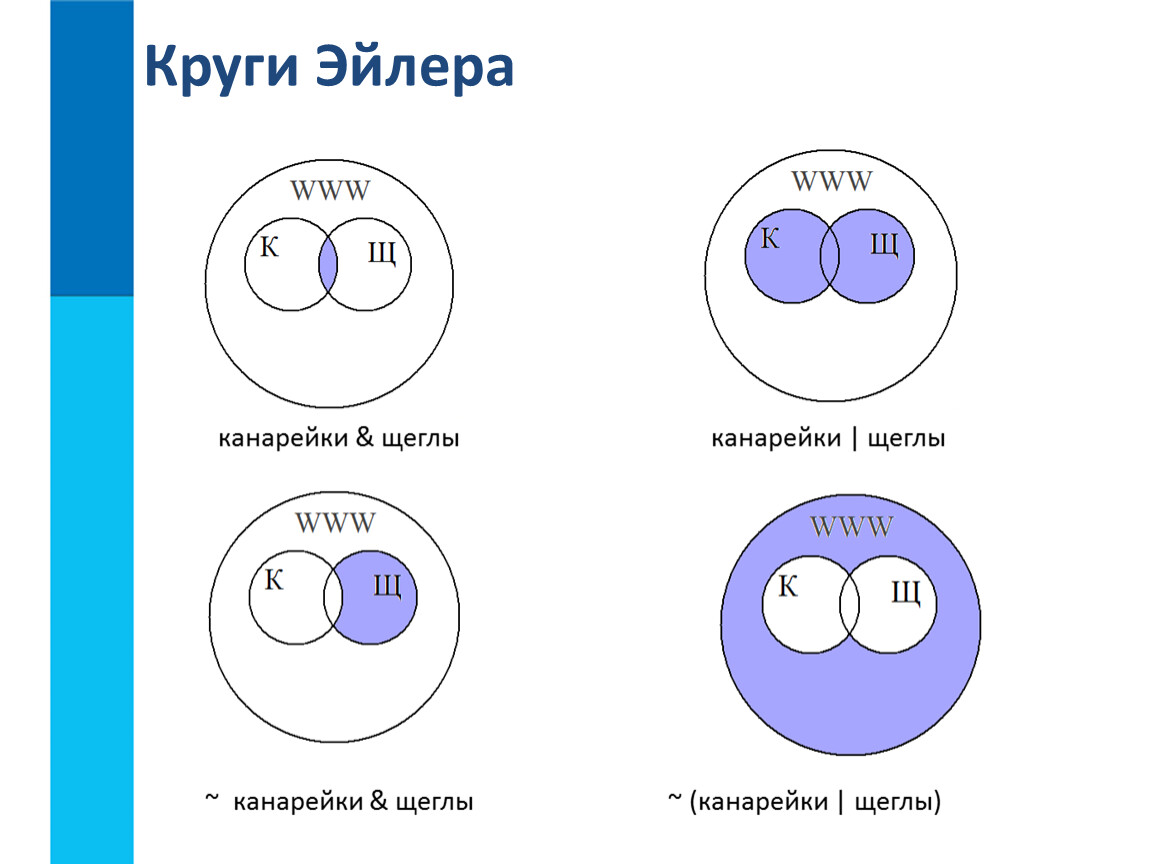
Используйте цвет для выделения отрицания: закрашивайте область, не входящую в множество, чтобы визуализация стала нагляднее.

Круги Эйлера за 3 минуты - ОГЭ по информатике 2024
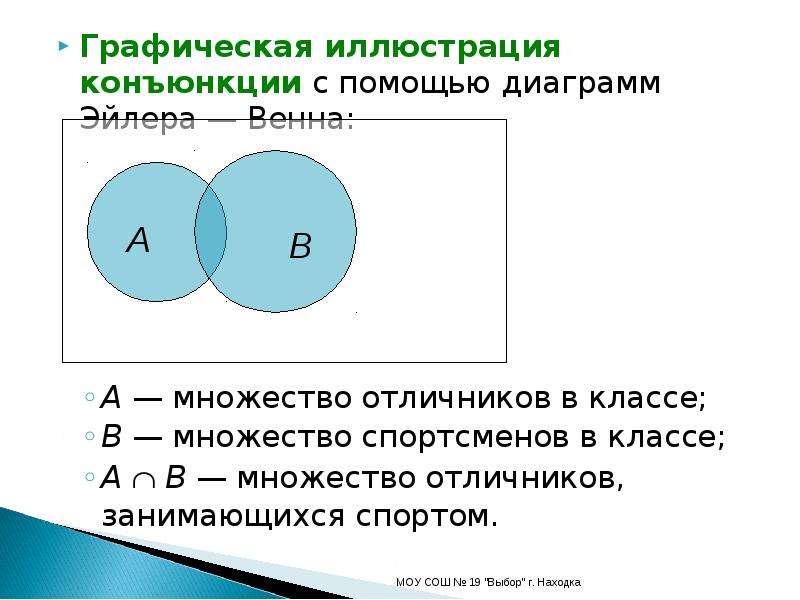
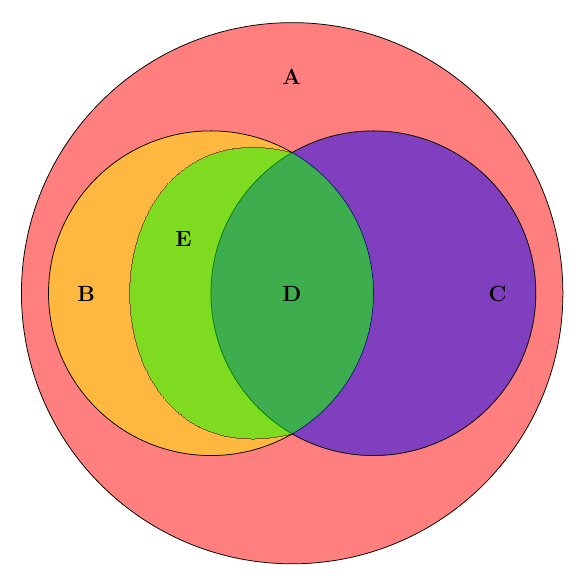
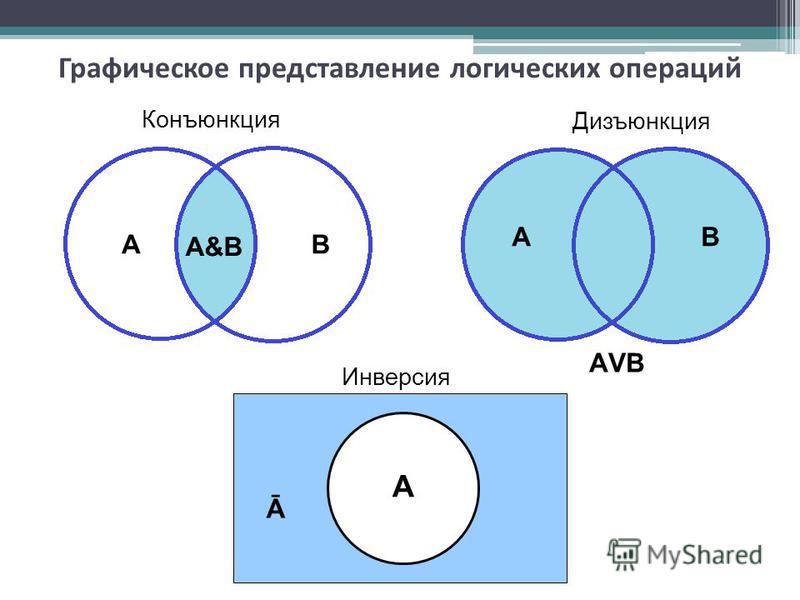
Обратите внимание на символику: знакомство с обозначениями, такими как ¬A (отрицание множества A), поможет точнее интерпретировать схемы.
Грамотное мышление. 3.1. Систематизация информации. Круги Эйлера.

Практикуйтесь с реальными примерами: создавайте круги для задач из повседневной жизни, чтобы лучше усвоить тему.

Круги Эйлера. Логическая задача на множества. Иностранные языки
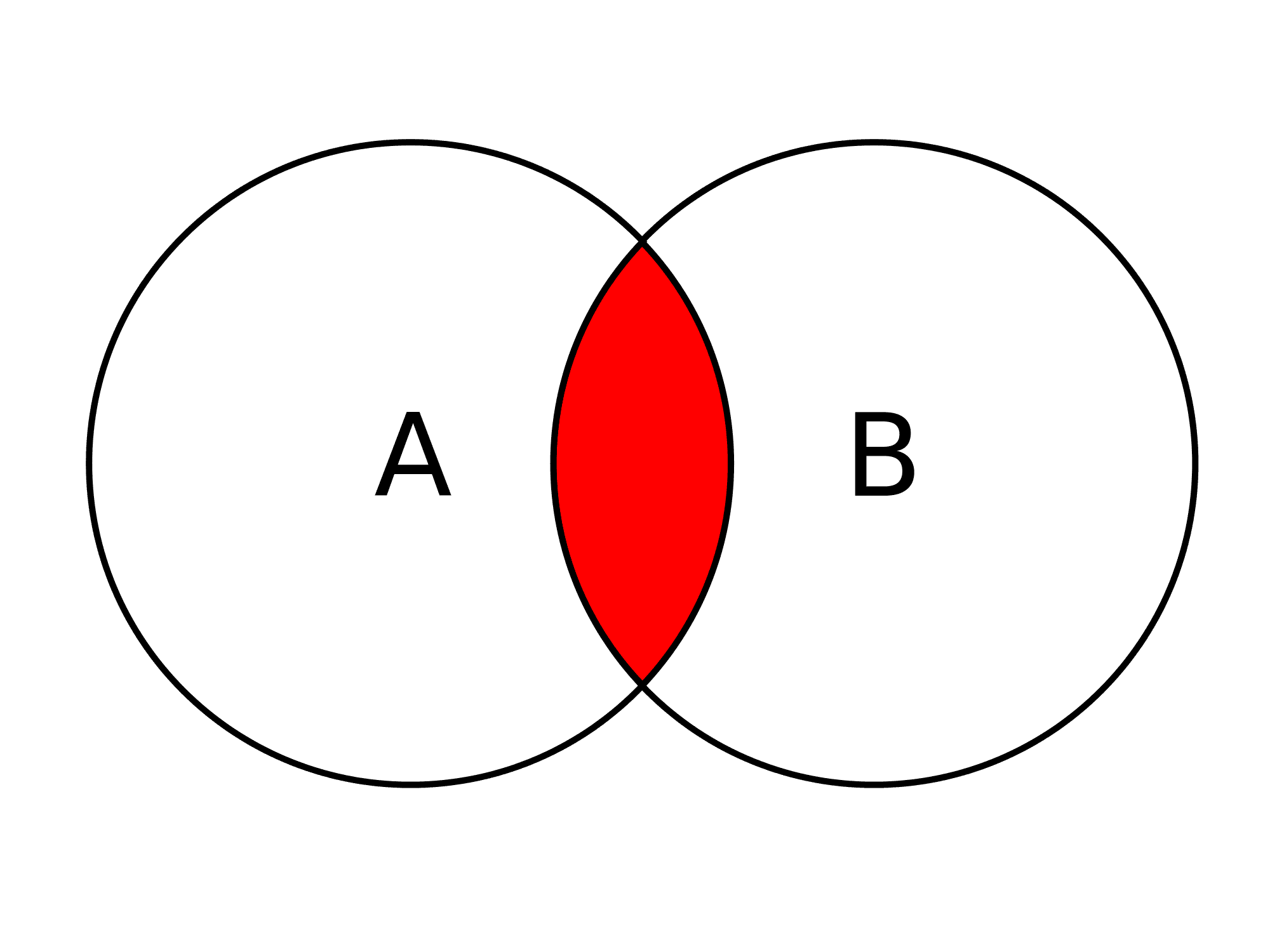
Сравните круги Эйлера и Венна: изучите, чем они отличаются, чтобы использовать наиболее подходящий инструмент для своих целей.

3 круга Эйлера
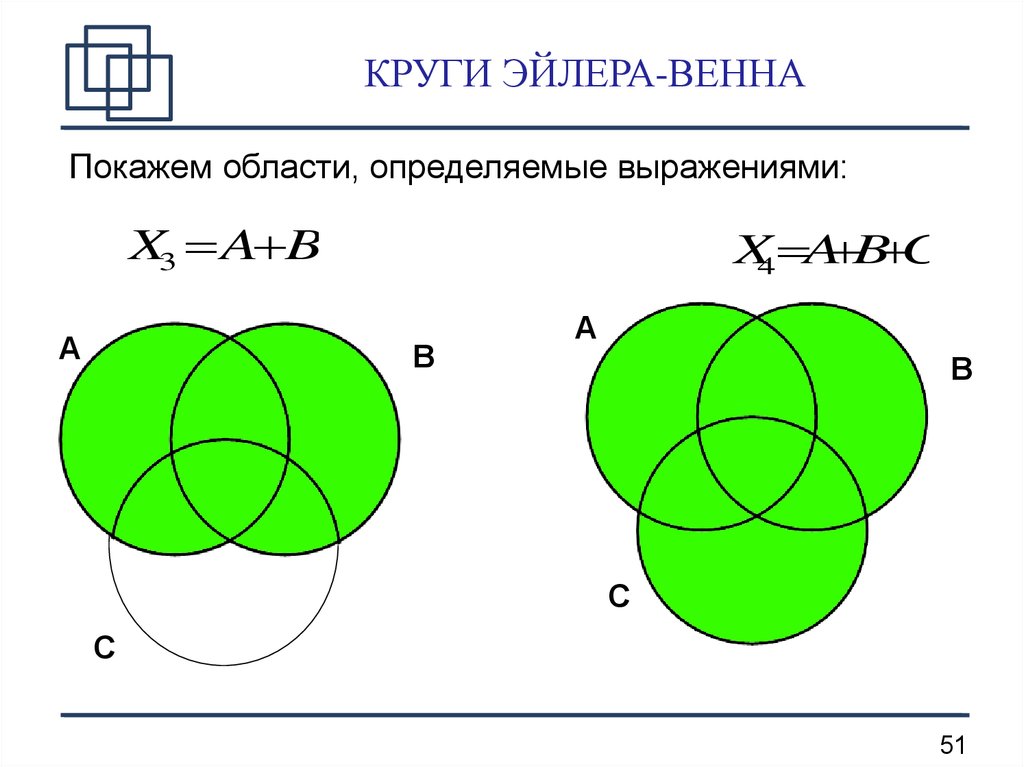
Используйте программные инструменты: такие программы, как PowerPoint или специальные онлайн-сервисы, помогут быстро создавать аккуратные схемы.
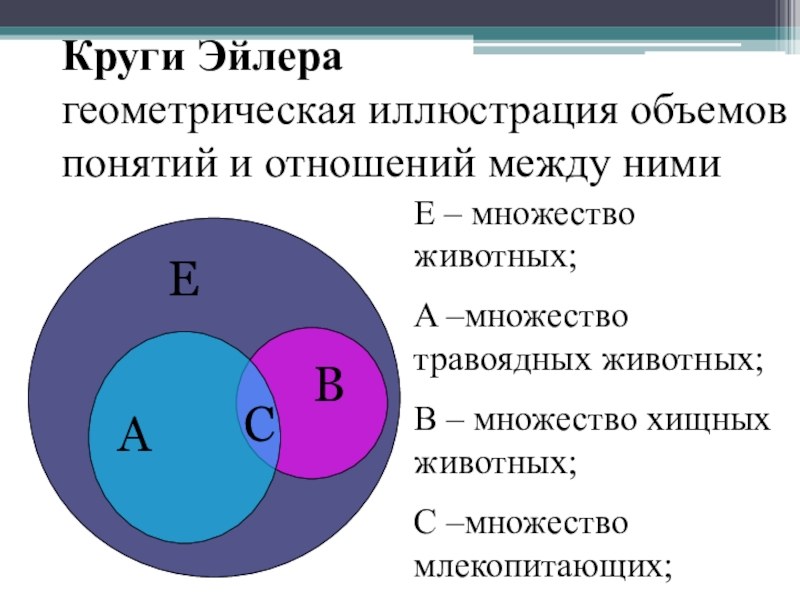

Чередуйте визуализацию с формулами: переход от графики к символике укрепляет понимание логики отрицания.

КРУГИ ЭЙЛЕРА 🤔 - математика #shorts
Изучите сложные примеры: скомбинируйте несколько множеств, чтобы понять, как отрицание влияет на их пересечения и объединения.

Круги Эйлера в реальной жизни. Математика на QWERTY
Обратитесь к учебной литературе: книги по логике часто содержат пояснения и задачи, полезные для изучения кругов Эйлера и Венна.
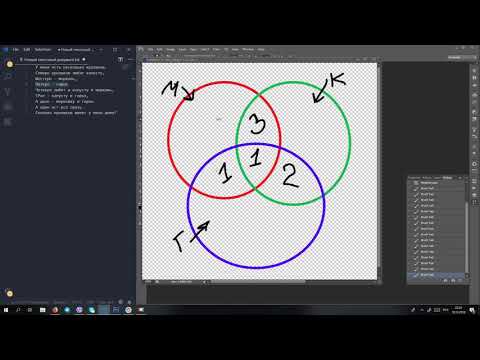
Простое объяснения решения задач при помощи кругов Эйлера