Основные методы нахождения корней характеристического уравнения в математике
Корни характеристического уравнения играют ключевую роль в анализе линейных динамических систем. Они помогают определить стабильность системы, поведение решения и другие важные параметры. Знание методов нахождения этих корней критично для специалистов в области математического моделирования и инженерии.


При решении характеристического уравнения используйте методы факторизации для упрощения вычислений.

Характеристическое уравнение в ДУ


Проверяйте дискриминант уравнения для понимания, какие типы корней вас ожидают.

2211 ЛОДУ. Корни характеристического уравнения комплексные и кратные.

Для сложных уравнений попробуйте использовать численные методы, такие как метод Ньютона.

2187. ЛОДУ. Корни характеристического уравнения действительные, не кратные.
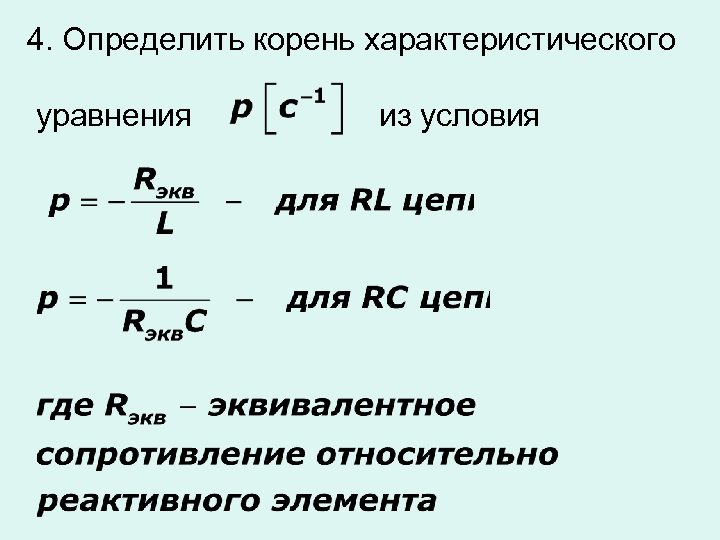

Не забывайте о комплексных корнях, если у уравнения есть отрицательные или нулевые собственные значения.

Повысь свой уровень по теме КОРНИ - Математика - TutorOnline
Использование графиков поможет визуализировать поведение корней для разных коэффициентов уравнения.

УДИВИТЕЛЬНЫЙ способ решения уравнения ★ Вы такого не видели! ★ Уравнение четвертой степени


Убедитесь, что корни характеристического уравнения соответствуют требованиям модели или системы.

2194. ЛОДУ. Корни характеристического уравнения комплексные и действительные.
Помните, что кратные корни могут повлиять на устойчивость системы, особенно в случае с диагонализируемыми матрицами.

В случае многомерных систем воспользуйтесь вычислительными средствами, чтобы ускорить нахождение корней.
Сеточные методы решения дифференциальных уравнений в частных производных.

Корни характеристического уравнения важны не только для анализа, но и для проектирования системы с нужными характеристиками.
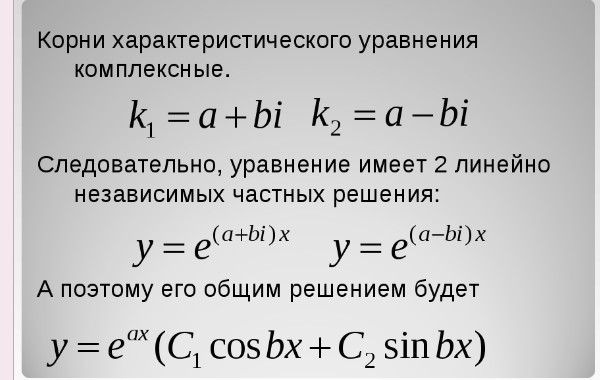

После нахождения корней всегда проверяйте результаты, подставив их обратно в исходное уравнение для проверки точности.

Как решать уравнения по схеме Горнера
