Как использовать комбинаторные схемы для расчёта вероятности и статистики

Комбинаторные схемы играют ключевую роль в теории вероятности и позволяют решать различные задачи, связанные с подсчётом вероятностей, вариантов выбора и распределений. В данной подборке представлены полезные советы и примеры, которые помогут вам лучше понять, как использовать эти методы на практике. Узнайте, как комбинировать различные элементы для нахождения точных решений и анализа ситуаций.

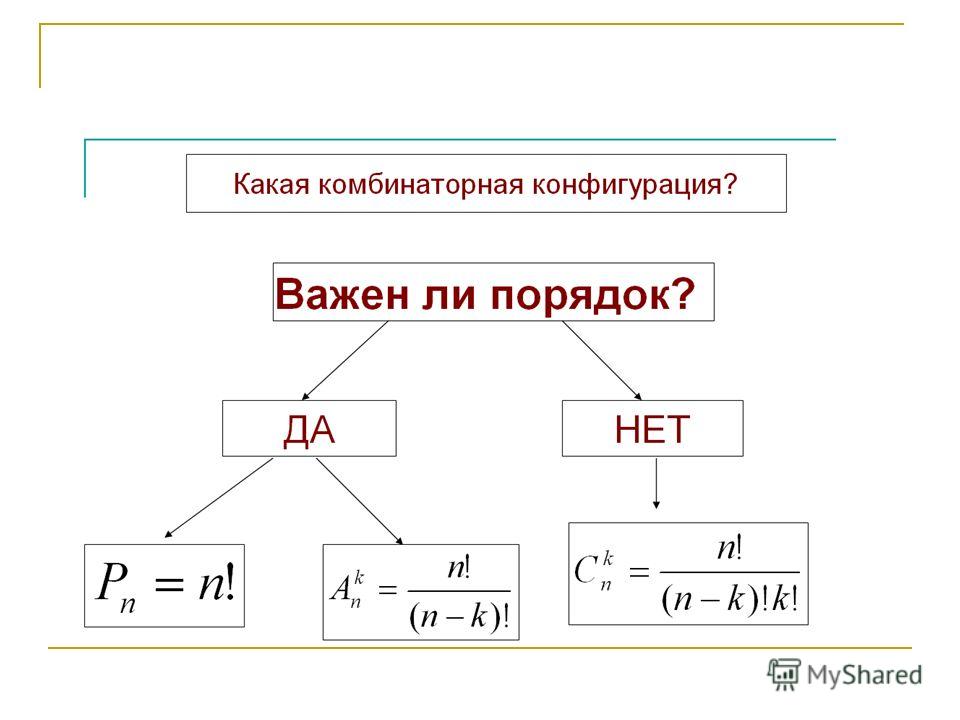
Изучите основные типы комбинаторных схем, такие как перестановки, сочетания и размещения, чтобы лучше понимать, как они применяются к задачам вероятности.

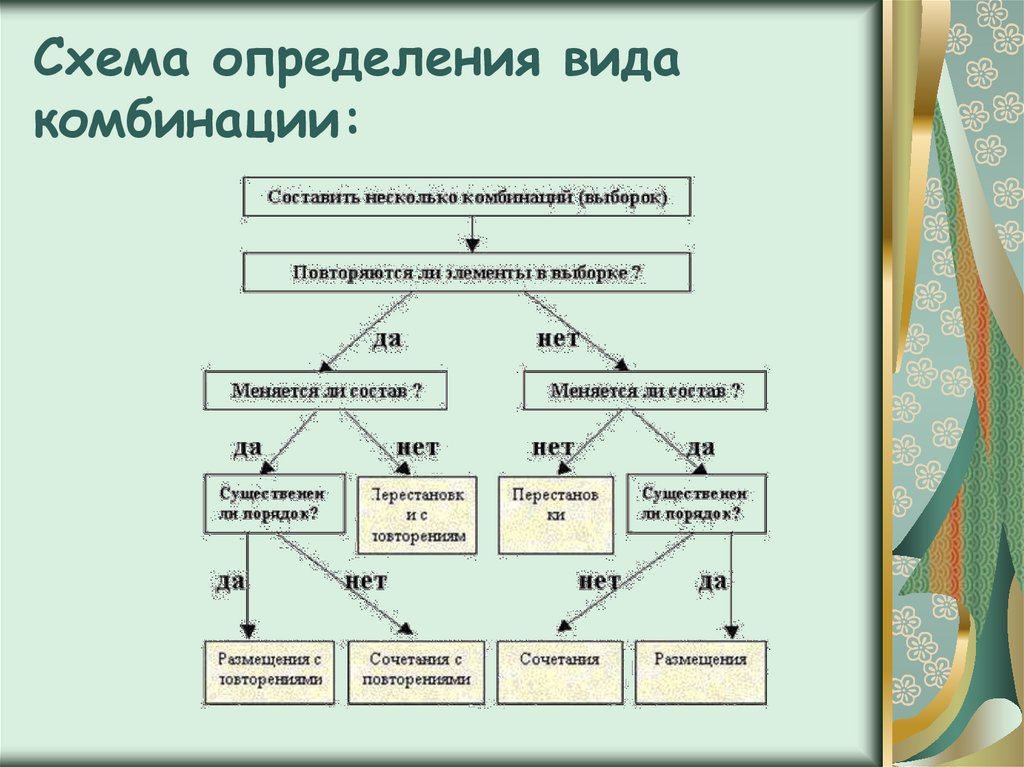
При решении задач важно помнить о принципе умножения и принципе сложения, которые позволяют комбинировать различные варианты в зависимости от условий задачи.

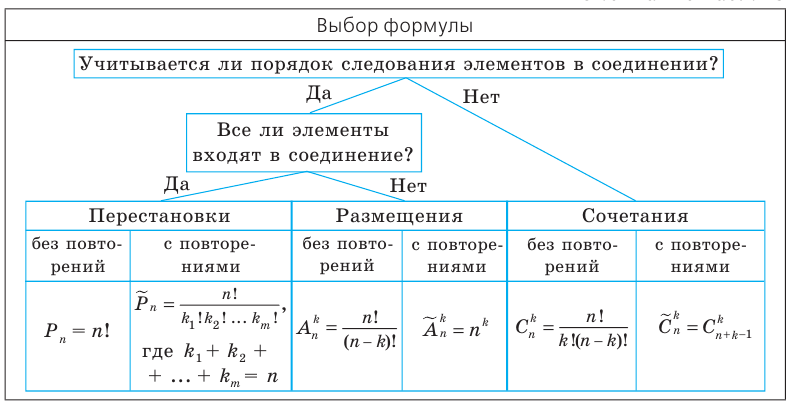
Не забывайте о биномиальном коэффициенте, который используется для подсчёта числа сочетаний. Это ключевой инструмент в задачах с вероятностями.

Для более сложных задач, попробуйте применять теорему о полной вероятности, которая помогает вычислить общую вероятность события, учитывая все возможные пути его наступления.

Для вычисления вероятности последовательных событий всегда учитывайте зависимость или независимость этих событий, что может значительно упростить решение.

Помимо классических методов, используйте графические представления комбинаторных схем, чтобы наглядно понять, как устроены различные варианты распределений.

При решении задач с большим числом вариантов полезно использовать симметричные свойства комбинаторных схем для упрощения подсчёта.

Уделяйте внимание ограничениям на элементы комбинаторных схем, например, если элементы не могут повторяться, это сильно изменяет подход к задаче.

Перед решением задачи тщательно формулируйте условия и проверяйте, являются ли события независимыми или зависимыми, так как это влияет на метод расчёта.

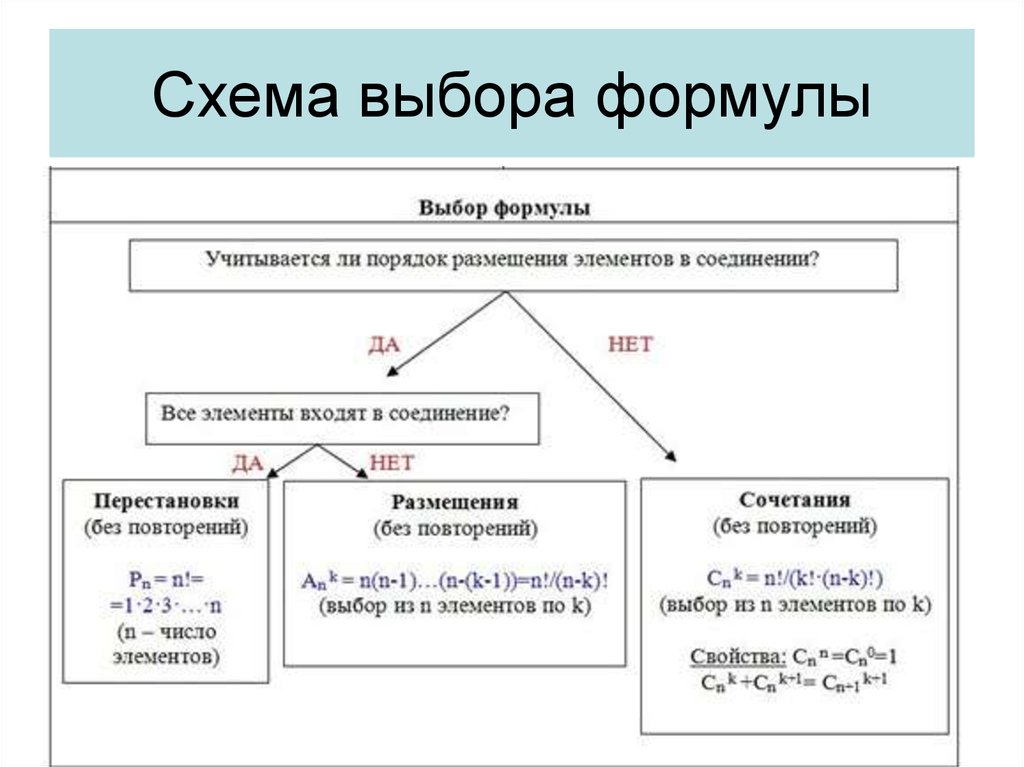
Регулярно практикуйтесь с различными примерами, чтобы закрепить навыки и уверенно решать задачи, используя комбинаторные схемы в теории вероятности.