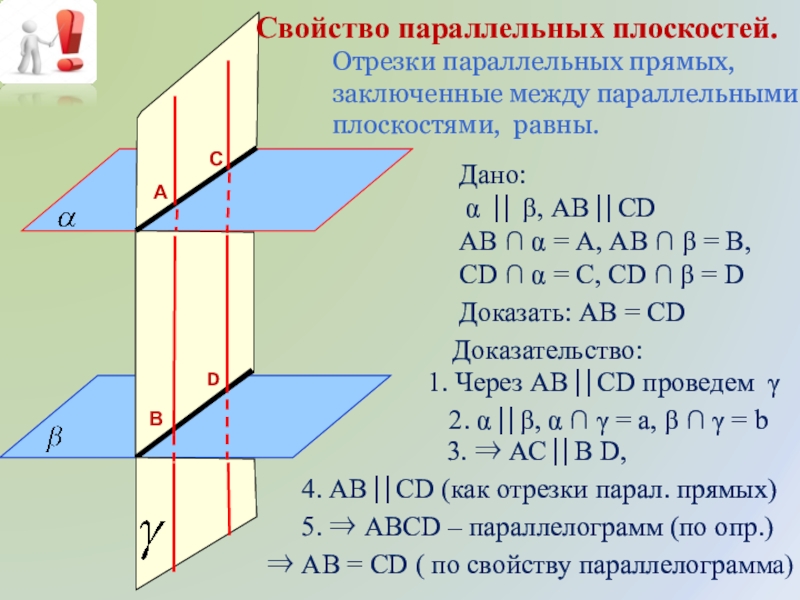
Основные способы и приемы доказательства параллельности плоскостей в Кубе с примерами решений

Доказательство параллельности плоскостей в Кубе является важной задачей в геометрии, которая помогает лучше понять пространственные отношения и свойства многогранников. На этой странице представлены различные методы и советы, которые помогут вам успешно решить эту задачу, а также научиться правильно применять геометрические принципы при работе с Кубом.

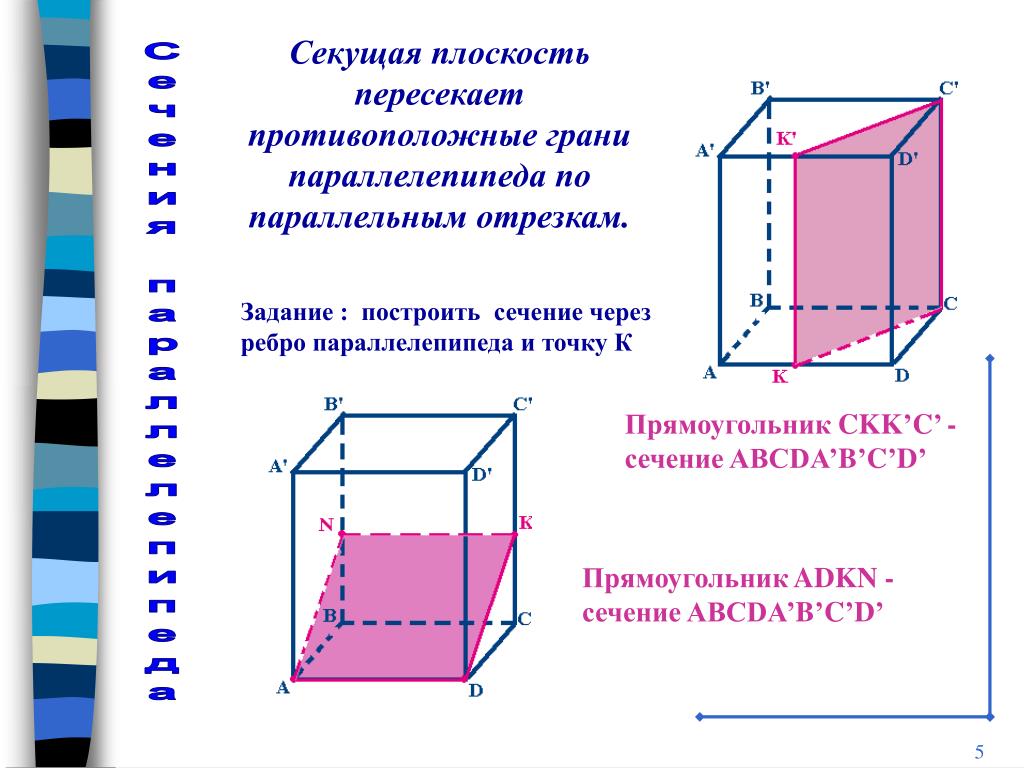
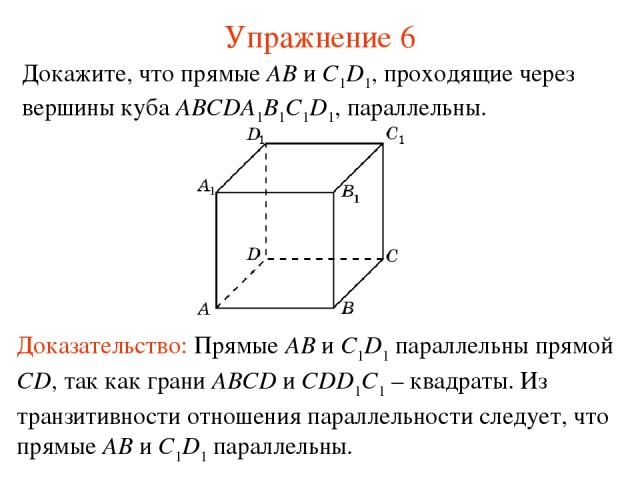
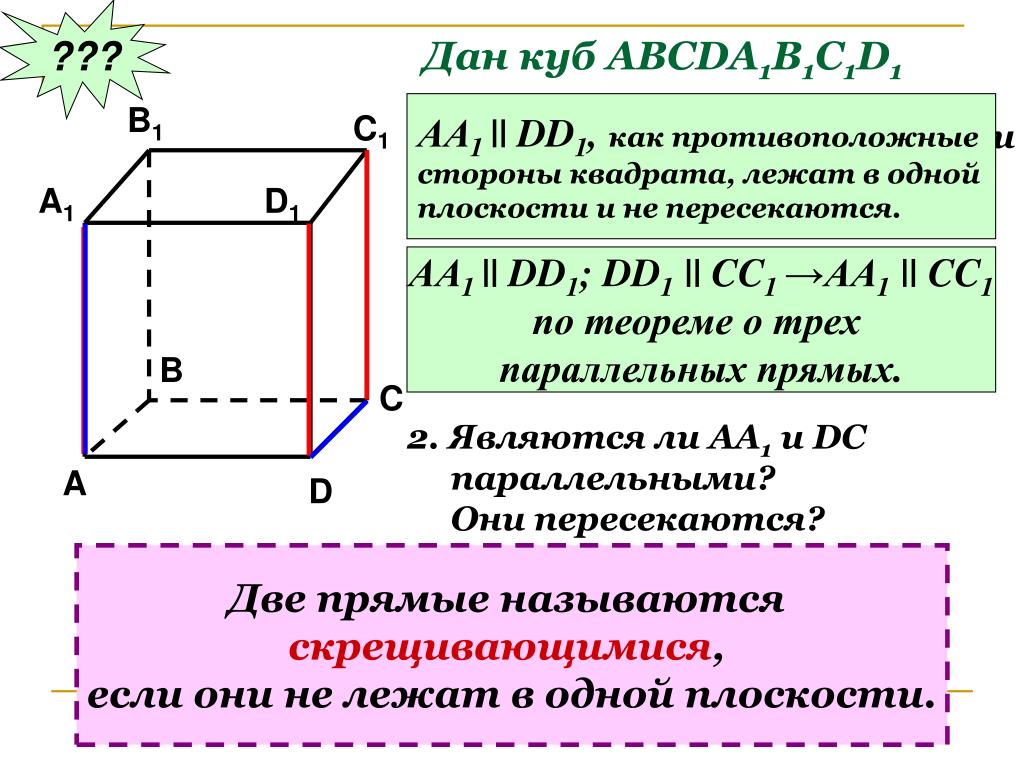
Для доказательства параллельности плоскостей важно обратить внимание на векторы нормалей к этим плоскостям: если векторы нормалей одинаковы или пропорциональны, то плоскости параллельны.

Использование координатных методов позволяет точно и наглядно вычислить уравнения плоскостей, что значительно упрощает задачу доказательства их параллельности.

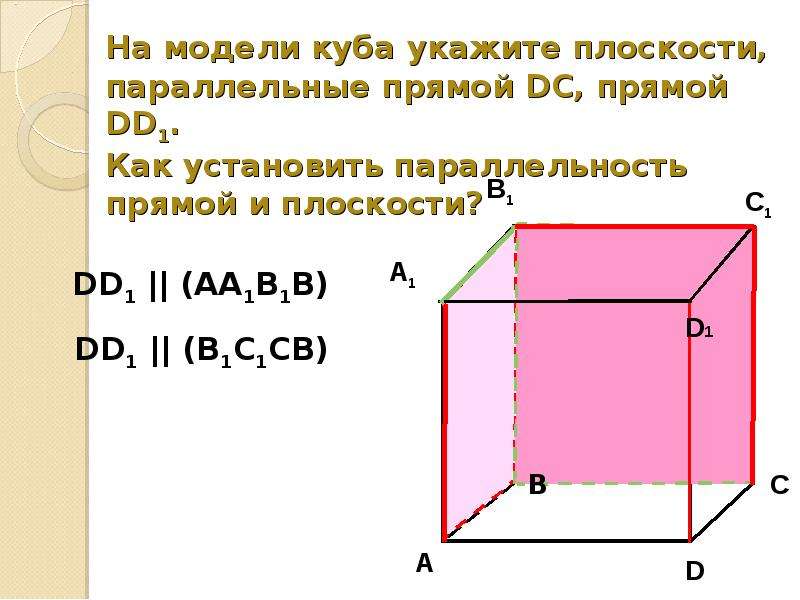
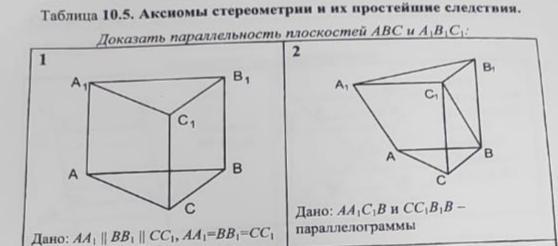
При доказательстве параллельности двух плоскостей в Кубе стоит использовать симметрию фигуры, чтобы уменьшить количество вычислений и шагов в решении.

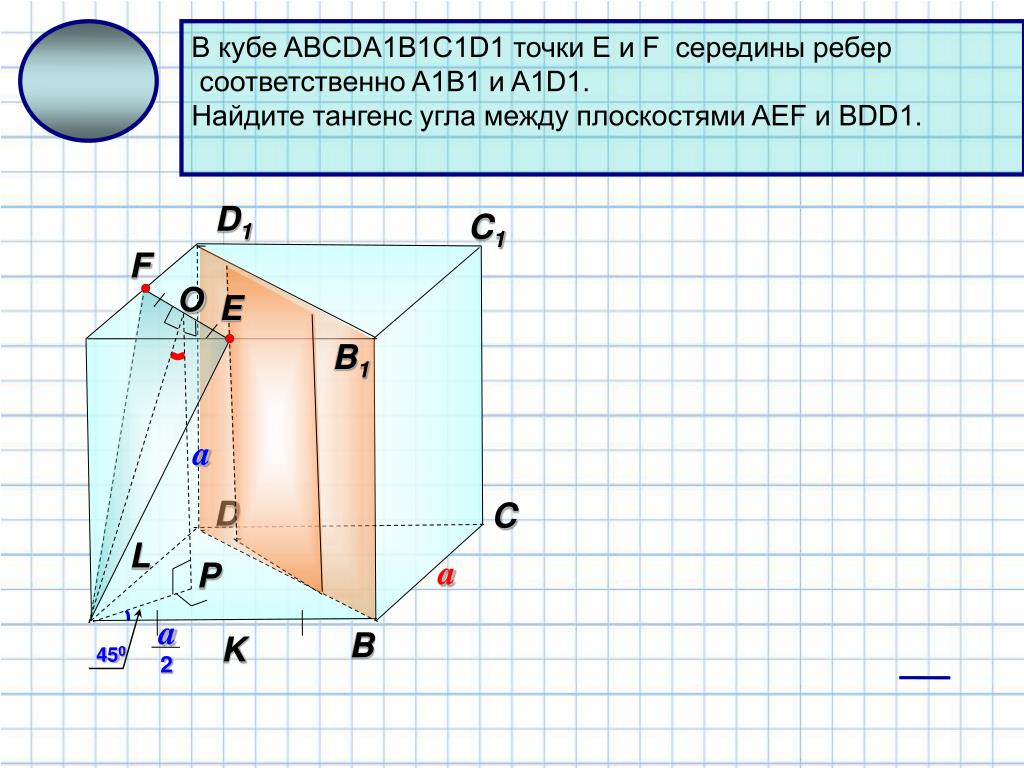
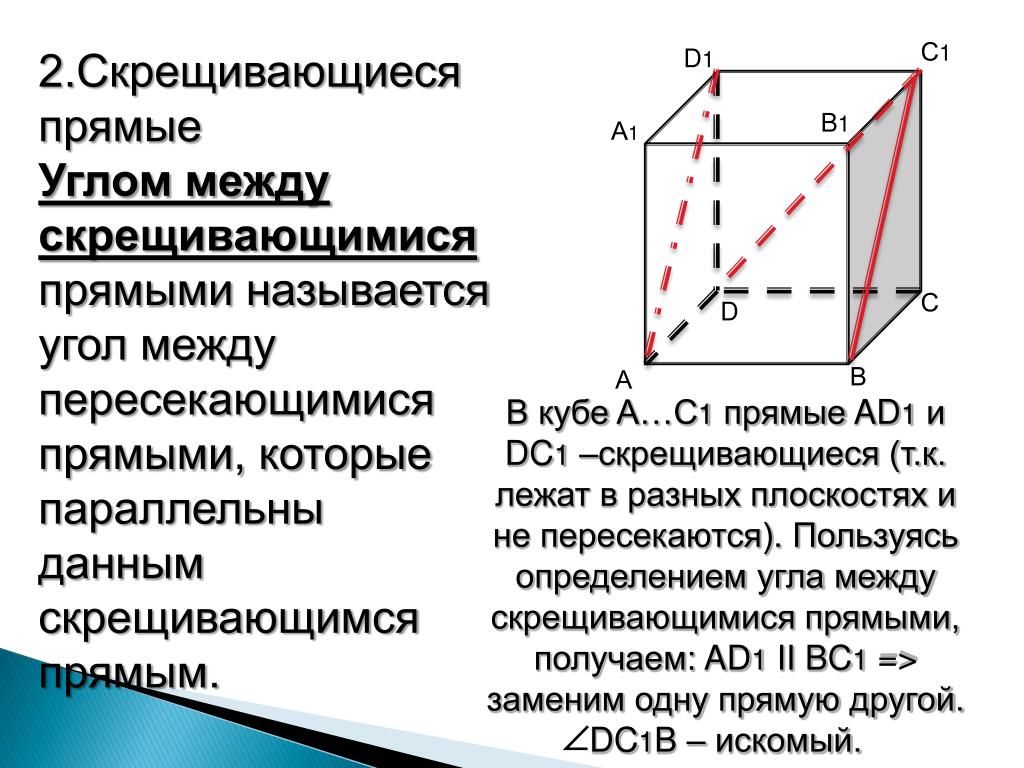
Важным методом является рассмотрение пересечений плоскостей с гранями Куба: если пересечения не меняются при движении вдоль одной оси, плоскости параллельны.

Для более сложных задач можно использовать метод векторных произведений, чтобы показать, что плоскости не пересекаются и расположены параллельно.

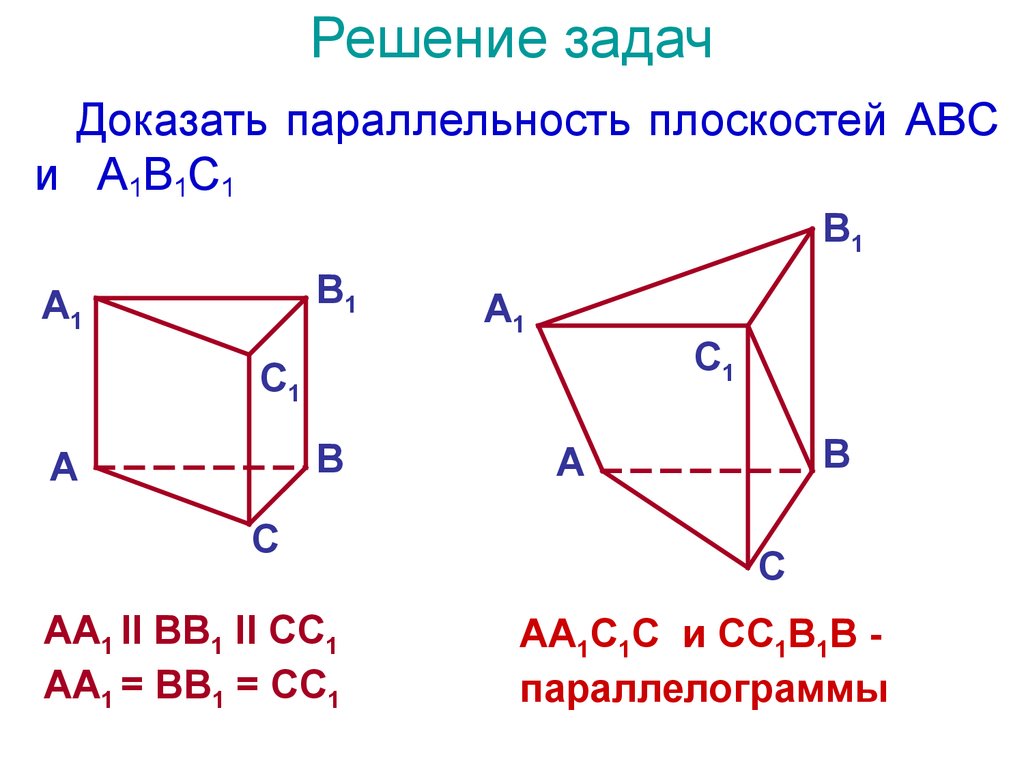
Если плоскости пересекаются в прямой, то они не могут быть параллельными. Это следует учитывать при решении задач на параллельность плоскостей.

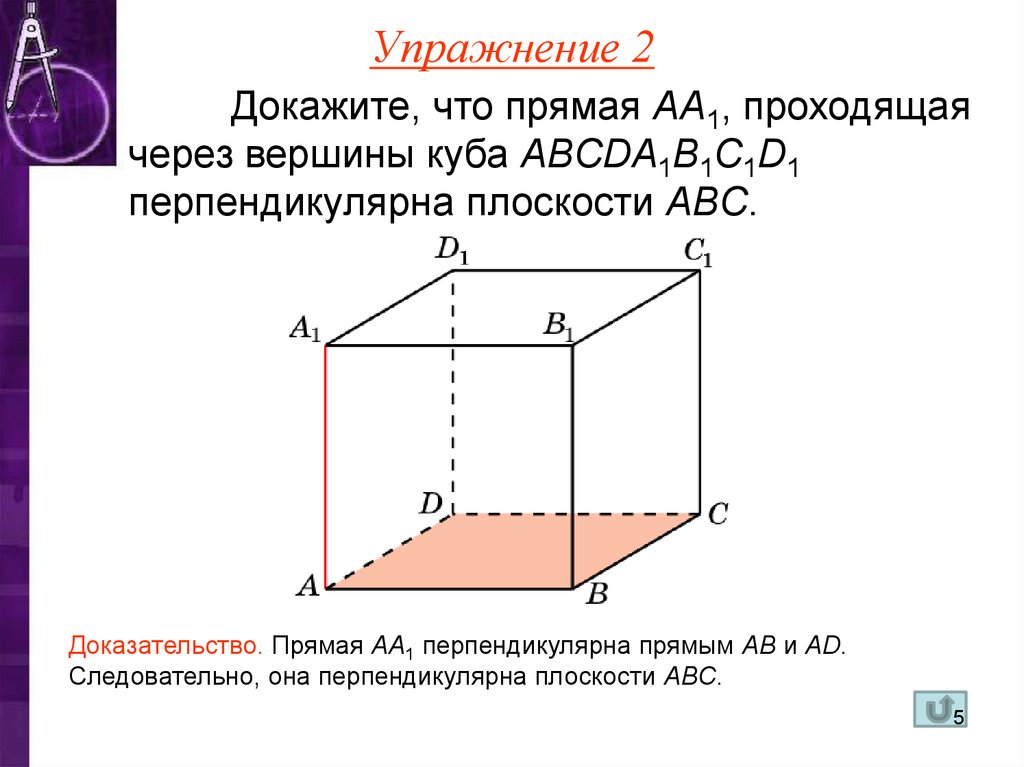
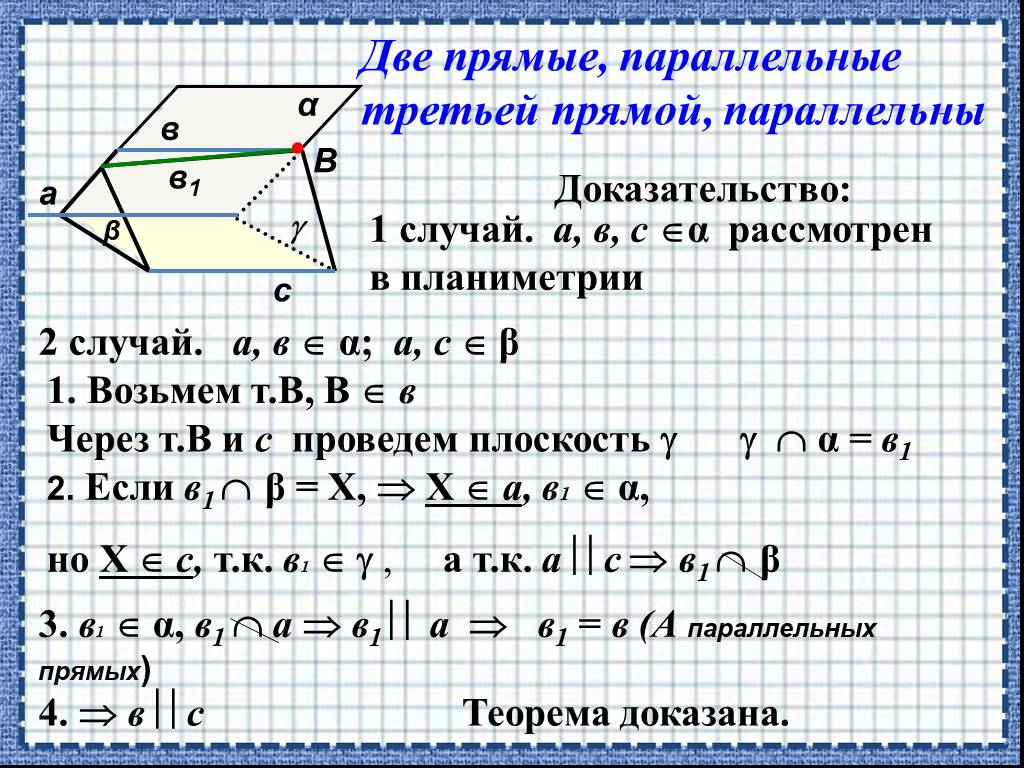
Использование диагоналей Куба и их свойств позволяет визуализировать отношения между плоскостями и их параллельность.

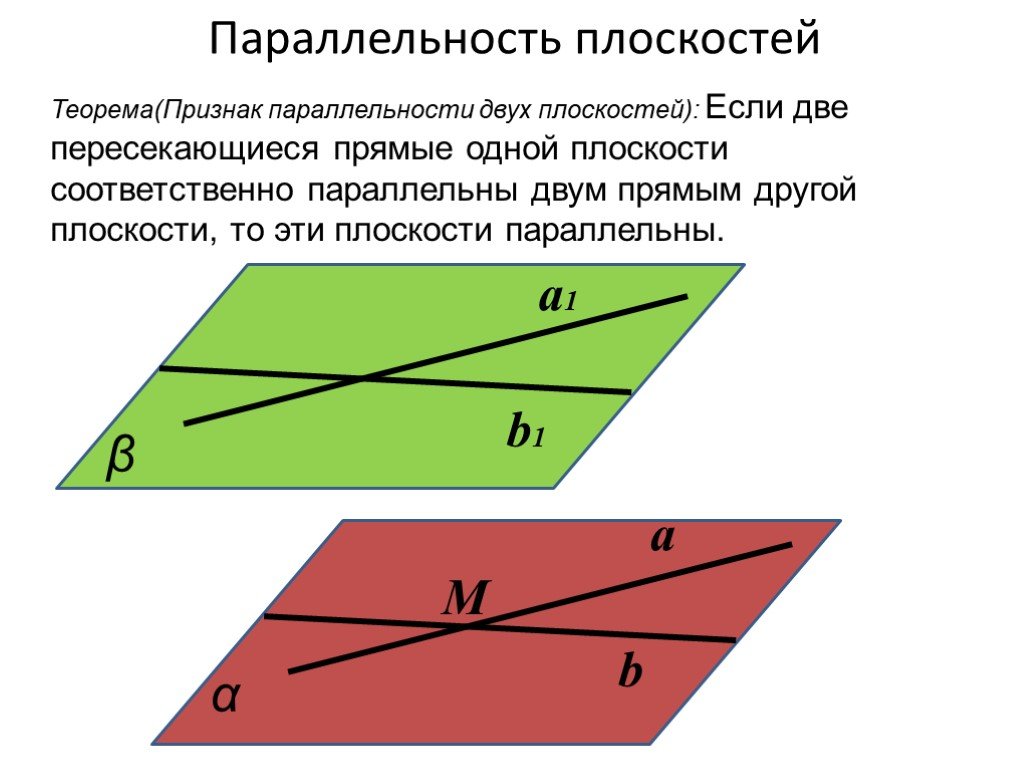
Для доказательства параллельности плоскостей в Кубе можно также использовать теоремы о прямых и плоскостях, такие как теорема о параллельности прямых, лежащих в параллельных плоскостях.

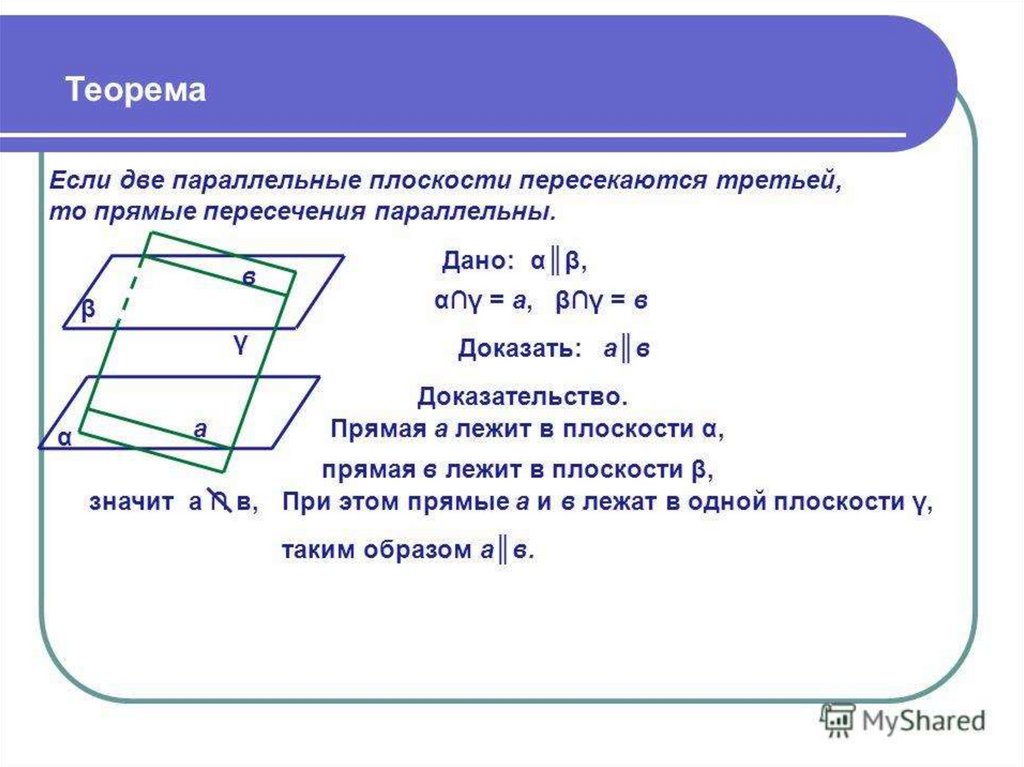
Обратите внимание на взаимное расположение плоскостей: если одна плоскость перпендикулярна двум пересекающимся прямым, а другая плоскость перпендикулярна этим же прямым, то плоскости параллельны.

На практике удобно использовать графические методы для проверки параллельности плоскостей: построив модель Куба, можно визуально оценить, параллельны ли плоскости.