Как правильно применять формулы первообразных функций: советы и рекомендации для студентов
На этой странице вы найдете подборку полезных советов и фотографий, которые помогут вам разобраться с формулами первообразных функций. Мы собрали информацию, которая будет полезна как новичкам, так и тем, кто хочет углубить свои знания в математике. Пошаговые объяснения и практические примеры помогут вам лучше освоить этот важный раздел интегралов.

При решении задач на нахождение первообразной старайтесь сначала проанализировать вид функции, чтобы выбрать наиболее подходящий метод интегрирования.

Смысл интеграла и производной. В помощь студенту


Не забывайте о правилах интегрирования стандартных функций, таких как степенные, тригонометрические и экспоненциальные функции.
Первообразная. 11 класс.


Практикуйтесь в использовании подстановки и интегрирования по частям — эти методы часто встречаются в сложных задачах.

ВСЕ О ФУНКЦИЯХ - №11 ЕГЭ , №18 ЕГЭ - Ильич ЕГЭ Профильная математика -

Если задача содержит дроби или сложные выражения, рассмотрите возможность разложения на простые дроби перед интегрированием.
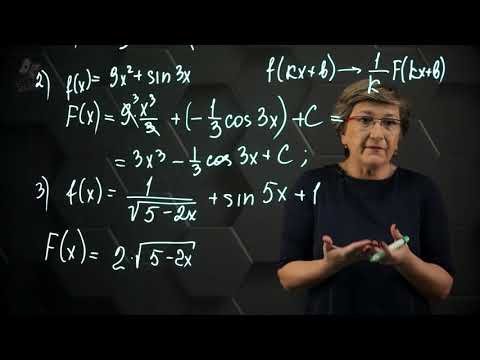
Первообразная. Практическая часть. 11 класс.

Обратите внимание на общие ошибки, такие как пропуск константы интегрирования или неправильная подстановка переменных.

Что такое первообразная функции
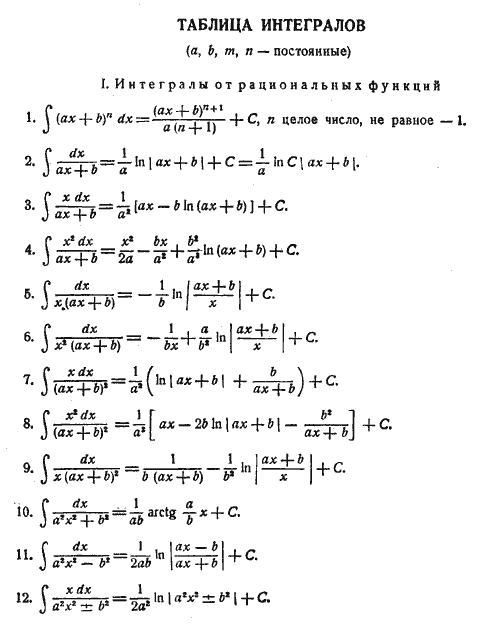
Используйте графики функций для лучшего понимания поведения первообразных, это поможет вам сориентироваться в решении задач.

Для проверки своих решений, сравнивайте результат с производной от найденной первообразной.

Первообразная. Практическая часть. 11 класс.

Помните, что для некоторых функций можно использовать таблицы первообразных, чтобы ускорить решение задач.

11 класс, 20 урок, Первообразная и неопределённый интеграл

РАЗБИРАЕМ ИНТЕГРАЛЫ ЧАСТЬ I #математика #егэ #огэ #Shorts #задачиегэ #формулы
Регулярно повторяйте изученный материал, чтобы закрепить знания о формулах и методах нахождения первообразных.

ПЕРВООБРАЗНАЯ ФУНКЦИИ решение примеров
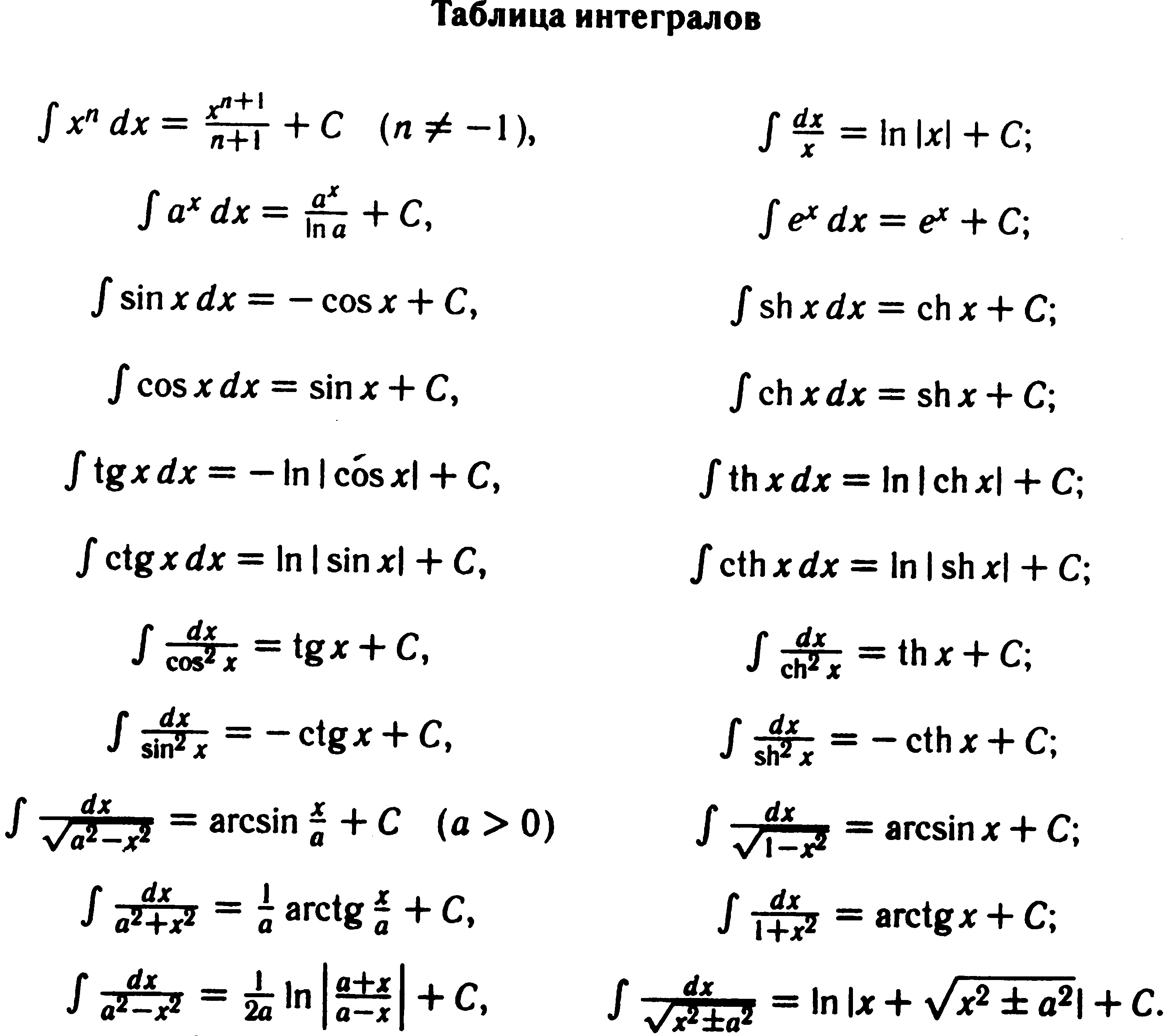
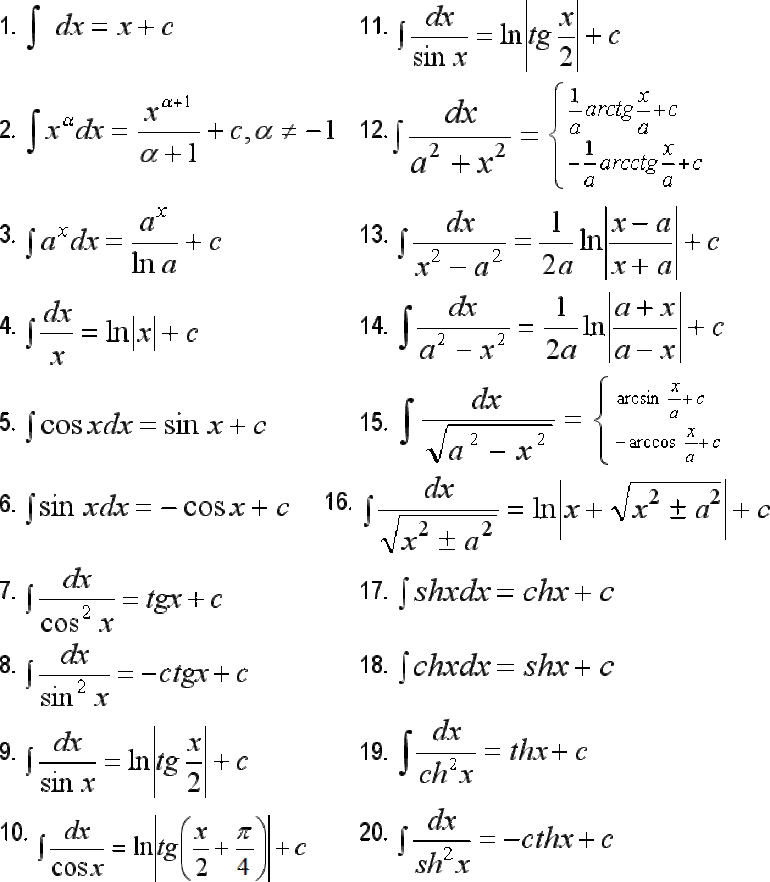
Не бойтесь ошибаться: ошибки — это неотъемлемая часть процесса обучения, и каждый неправильный шаг приближает вас к правильному решению.
Математика без ху%!ни. Интегралы, часть 1. Первообразная. Дифференцирование и интегрирование.
