Основы нахождения касательной линии с использованием производной функции
На данной странице представлена подробная информация о том, как найти формулу касательной к графику функции с использованием производной. Вы узнаете, как этот процесс связан с анализом функции и как правильно построить касательную линию в разных точках графика.
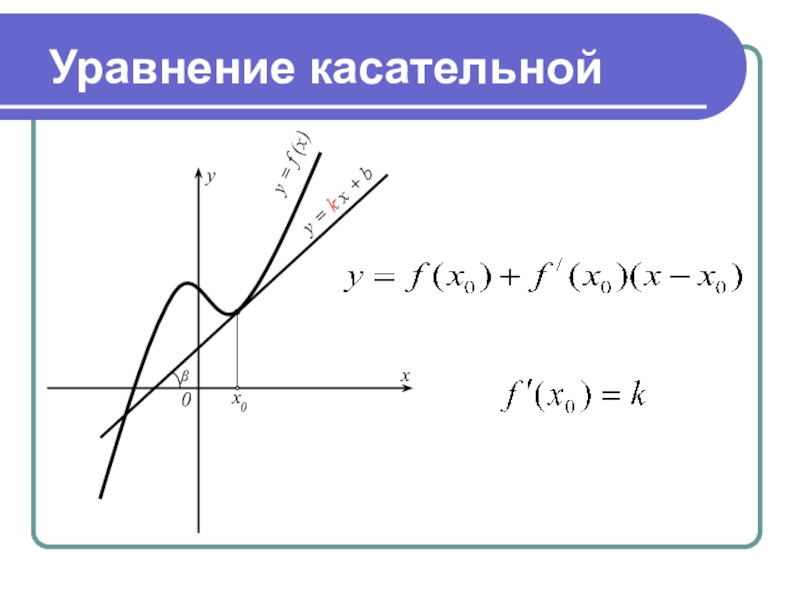

Для нахождения касательной важно правильно определить точку касания графика с прямой. Это точка, в которой график функции и касательная имеют одинаковое направление.

Производные с нуля до уровня ЕГЭ №8

При вычислении производной не забывайте о правилах дифференцирования для различных типов функций: степенных, тригонометрических и логарифмических.

Геометрический смысл производной - Касательная


Не путайте угловой коэффициент касательной с производной функции в данной точке. Производная в точке — это именно угловой коэффициент касательной линии.
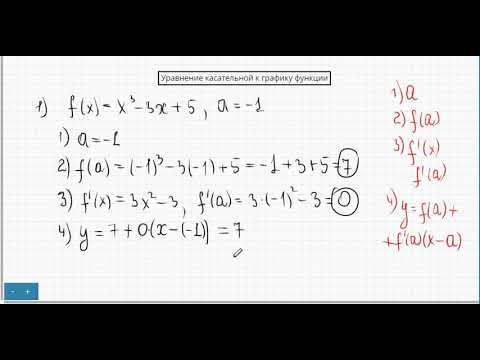
Уравнение касательной к графику функции

Если функция имеет сложную форму, попробуйте сначала упростить выражение, используя алгебраические преобразования, прежде чем дифференцировать.
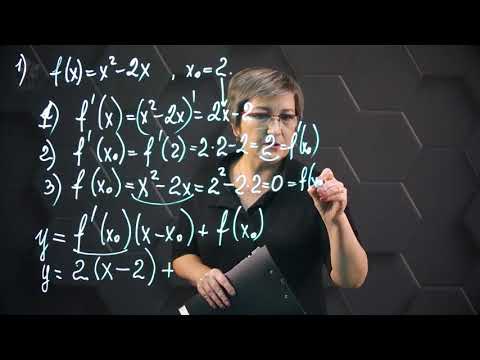
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.
Проверяйте вычисления через графическое представление. Иногда визуальная проверка помогает заметить ошибки при нахождении уравнения касательной.

Математика без Ху%!ни. Уравнение касательной.

Для точного нахождения касательной линии важно точно знать значения функции и её производной в нужной точке.
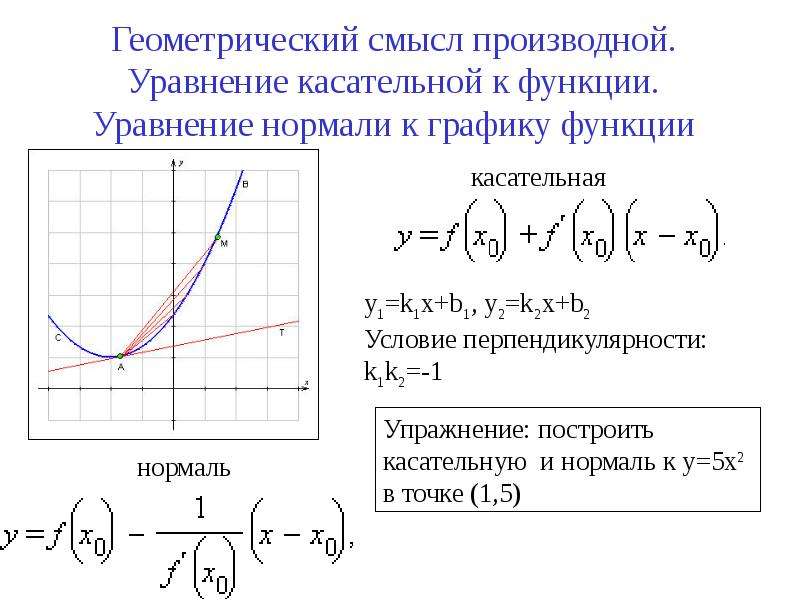
Обратите внимание, что касательная существует только в том случае, если производная функции в точке касания конечна. В противном случае касательная не будет определена.

Используйте правила дифференцирования для составных функций, такие как правило произведения и частного, если ваша функция имеет сложную структуру.

Уравнение касательной к графику функции - Алгебра 10 класс #45 - Инфоурок

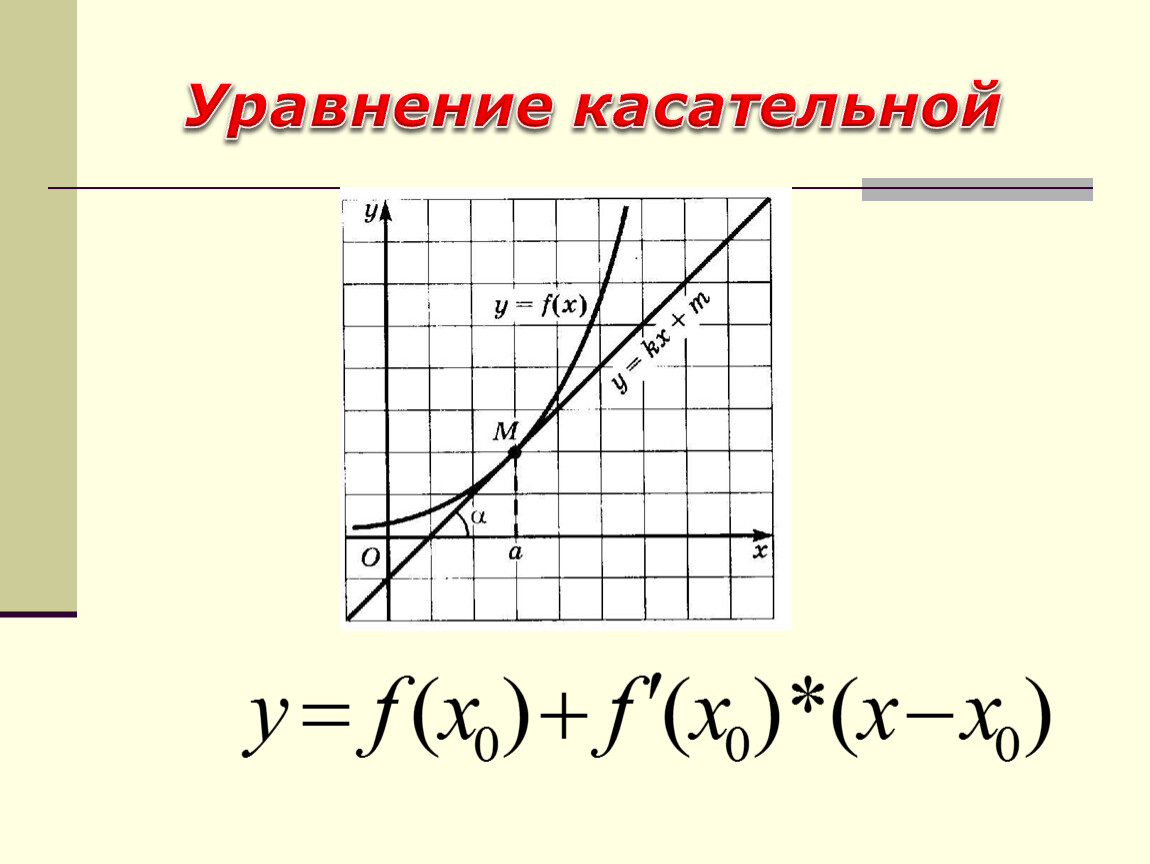
При работе с производной всегда учитывайте её значение в контексте задачи: она может быть использована для нахождения скорости изменения функции, а также для анализа её поведения.

Производная с нуля. Решаем 100+ задач из сборника Демидовича. Высшая математика
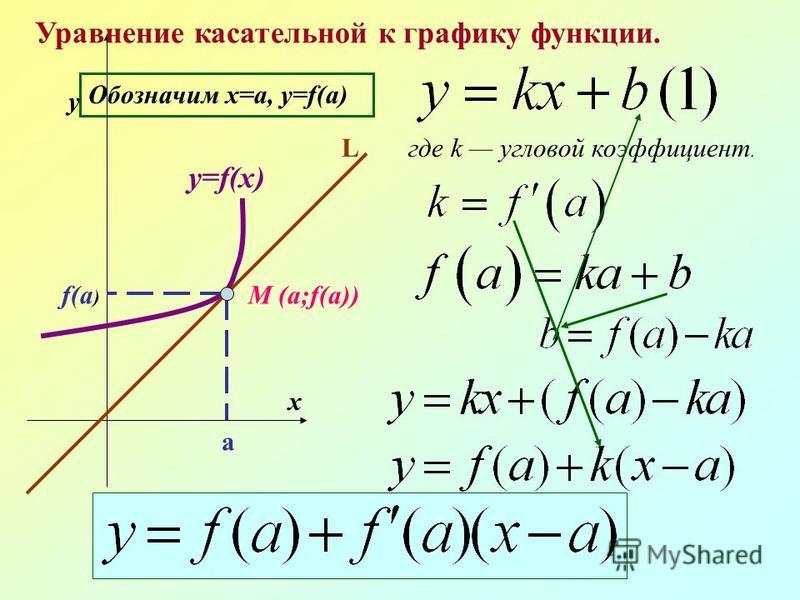

Для нахождения уравнения касательной нужно помнить, что её уравнение имеет вид: y - f(a) = f(a)(x - a), где a — точка касания графика функции.

10 класс, 43 урок, Уравнение касательной к графику функции


Как написать уравнения касательной и нормали - Математика