Основные принципы числовых последовательностей, ограниченных снизу, и их использование

Числовая последовательность, ограниченная снизу, играет важную роль в математическом анализе и теории чисел. Такие последовательности имеют нижнюю границу, которая обеспечивает их стабильность и помогает в различных вычислениях и доказательствах. В этой статье мы рассмотрим основные свойства этих последовательностей и предложим полезные советы для работы с ними.

Когда вы работаете с числовыми последовательностями, всегда проверяйте, есть ли у неё нижняя граница, чтобы избежать ошибок в дальнейших вычислениях.

Для определения нижней границы последовательности полезно использовать понятие инфимума, которое позволяет найти наименьшее возможное значение, к которому стремится последовательность.

В математике часто применяется принцип монотонности, который позволяет утверждать, что если последовательность монотонно возрастает и ограничена снизу, то она сходится.

Не забывайте, что если последовательность ограничена снизу, это не обязательно означает, что она сходится; она может быть расходимой, но всегда будет иметь предел сверху.

Для числовых последовательностей, ограниченных снизу, полезно знать свойства их предельных точек, поскольку это помогает в анализе их поведения на больших значениях.

Если вы хотите доказать, что последовательность сходится, проверьте, имеет ли она наименьшую возможную границу, к которой она стремится.

Для анализа последовательностей можно использовать теорему Больцано-Вейерштрасса, которая утверждает, что каждая ограниченная последовательность имеет хотя бы одну сходящуюся подпоследовательность.

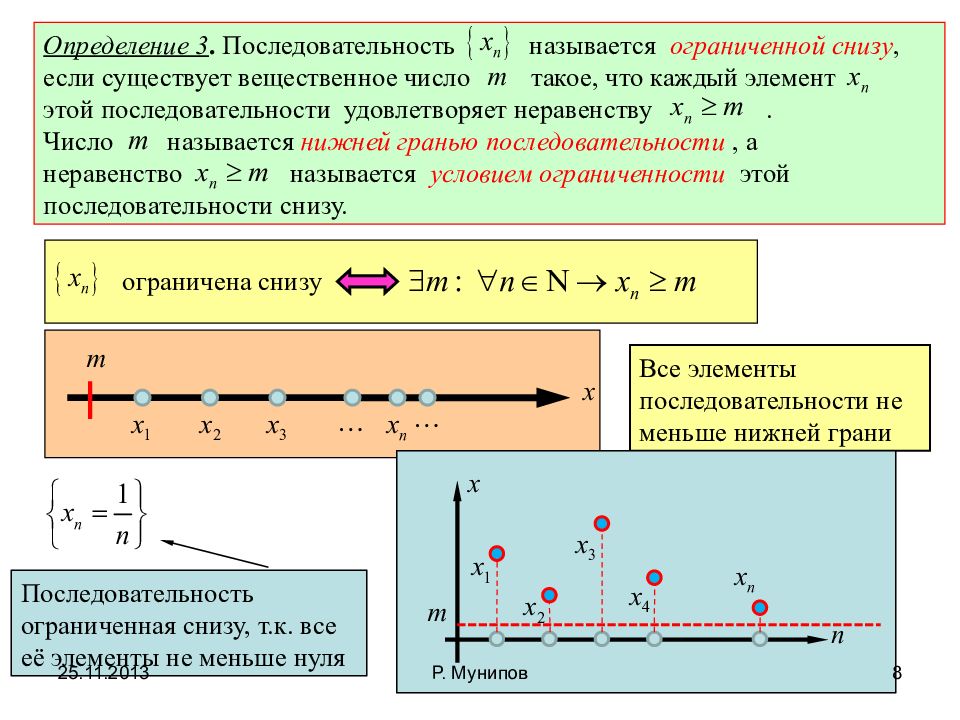
Понимание того, что последовательность ограничена снизу, помогает упростить доказательства в математическом анализе, например, при доказательствах теорем об ограниченности функций.

Если вам нужно вычислить предел последовательности, ограниченной снизу, попробуйте сначала найти её инфимум, а затем исследуйте её поведение при стремлении к бесконечности.

При работе с числовыми последовательностями важно учитывать их ограничения, чтобы избежать неверных интерпретаций при анализе их сходства или расходимости.