Как круги Эйлера помогают в алгебре логики: пошаговое руководство для новичков

Алгебра логики и круги Эйлера — мощные инструменты для решения логических задач. Эти графические представления помогают визуализировать сложные логические выражения и упрощают их анализ. В данной статье мы рассмотрим, как эффективно использовать круги Эйлера в логике, что позволит вам лучше понять основы и решить даже самые сложные задачи.

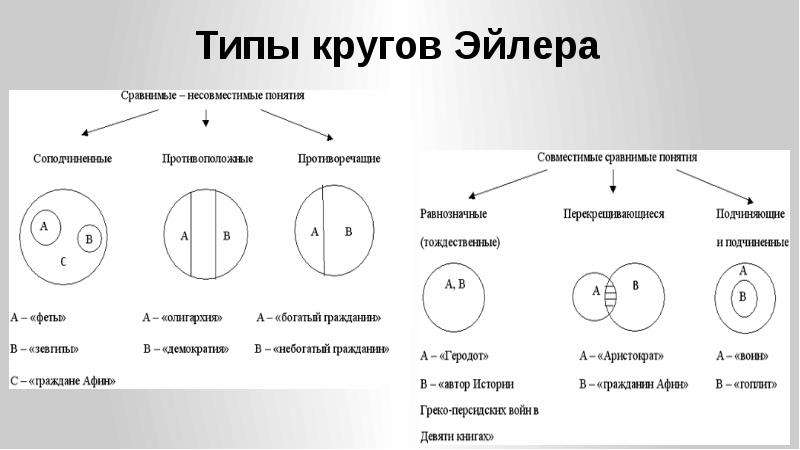
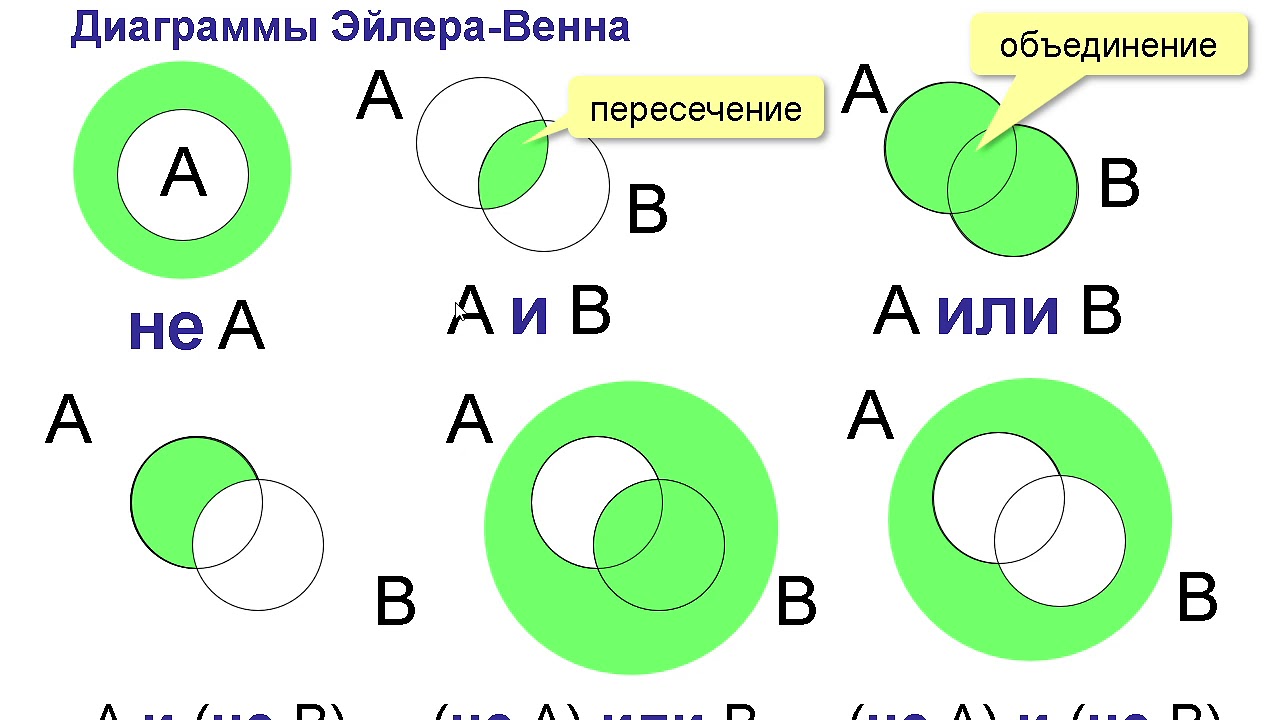
Для успешного применения кругов Эйлера важно понимать, как правильно интерпретировать пересечения множеств. Начните с простых примеров, чтобы привыкнуть к визуальному представлению логических операций.

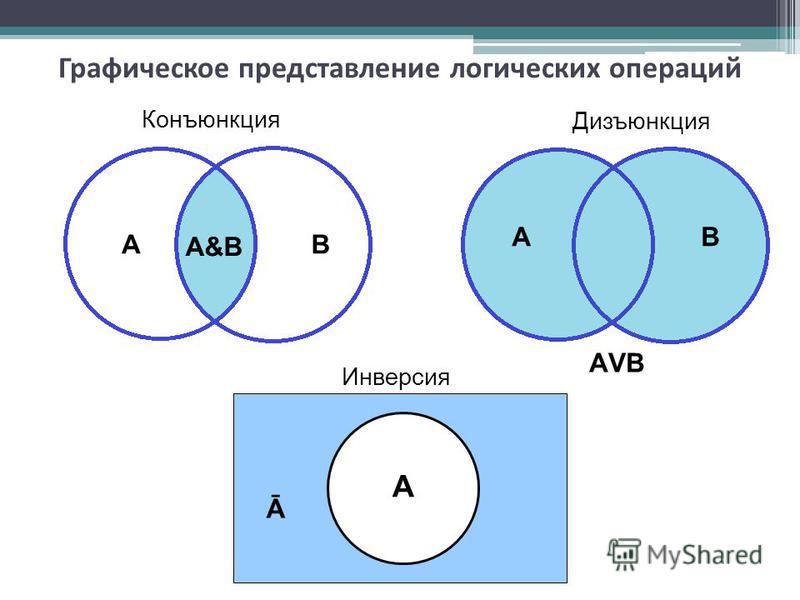
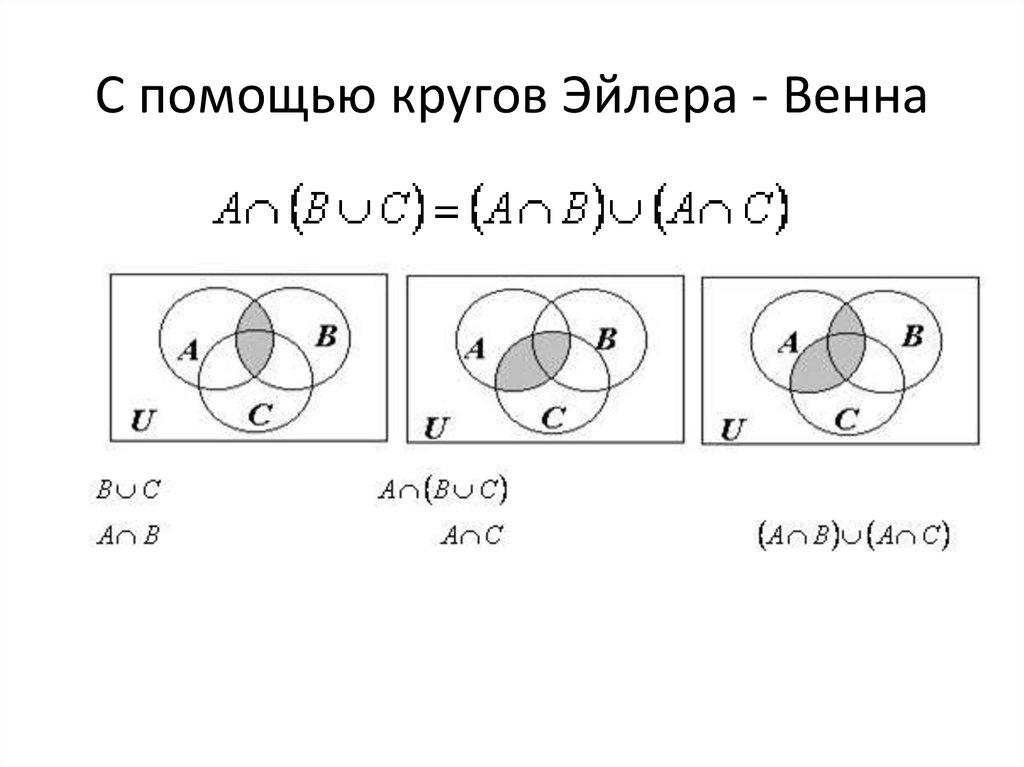
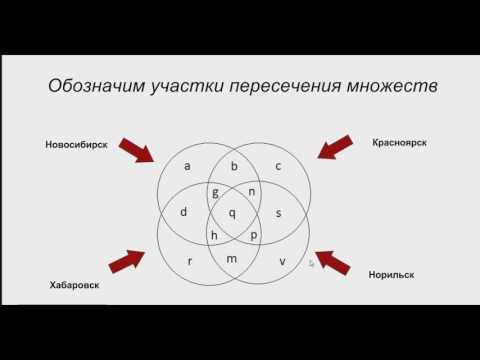
При работе с кругами Эйлера не забывайте учитывать все возможные пересечения между множествами. Каждое новое пересечение открывает новые возможности для решения задачи.

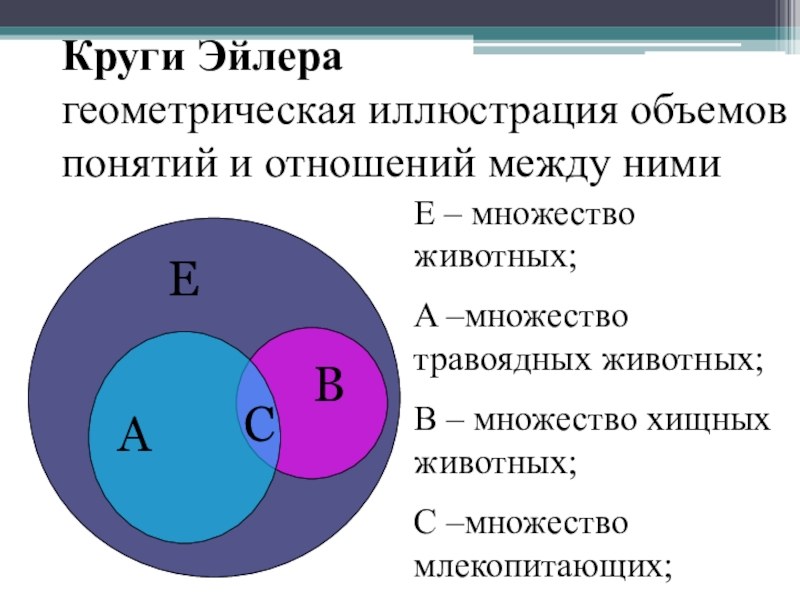
Для углубленного понимания алгебры логики рекомендуется изучать различные типы задач, в которых используются круги Эйлера. Это поможет вам увидеть разнообразие применения этого метода.

Не ограничивайтесь простыми примерами. Постепенно переходите к более сложным задачам, чтобы развивать логическое мышление и улучшать навыки работы с кругами Эйлера.

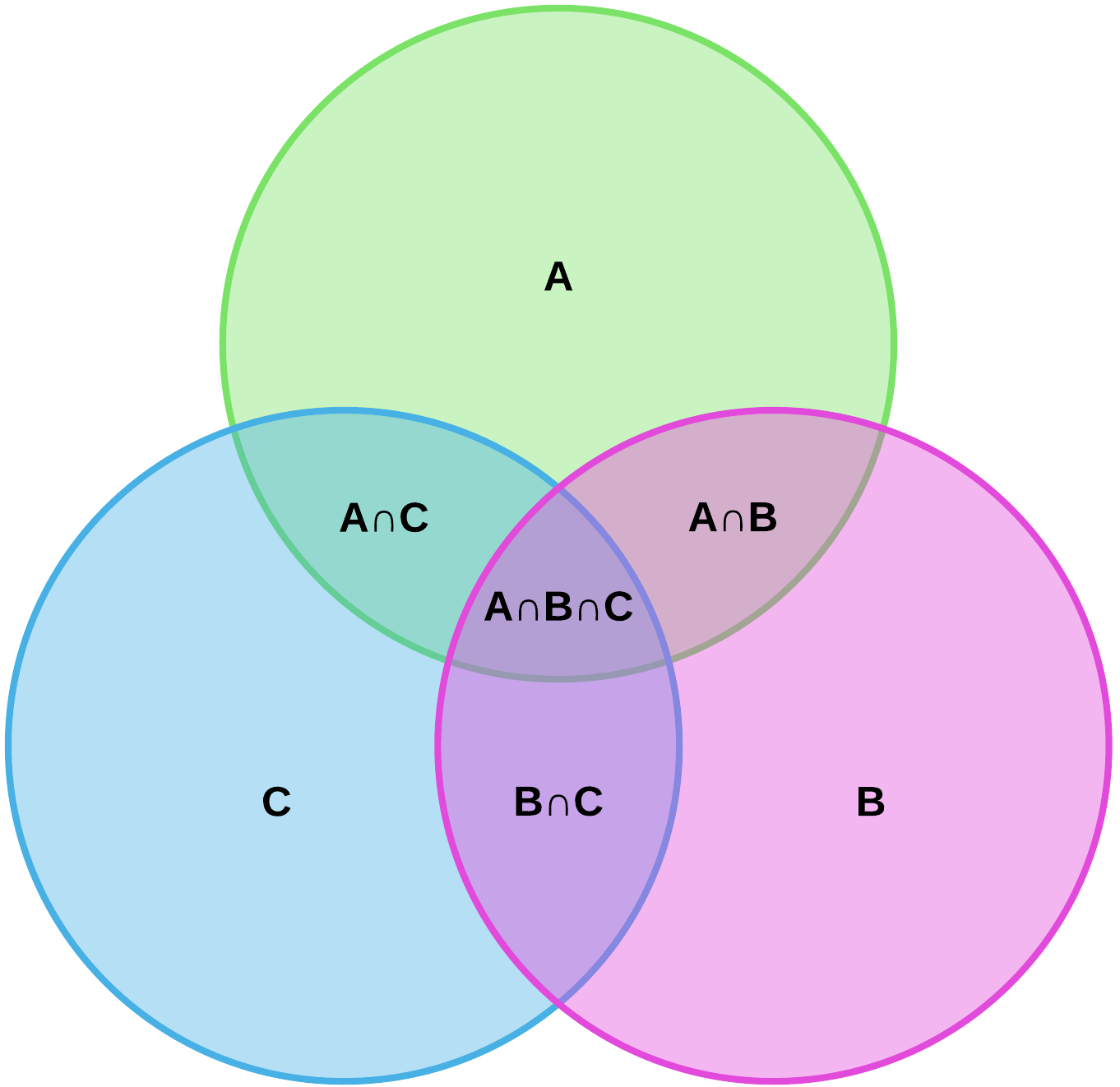
Попробуйте рисовать круги Эйлера на бумаге, чтобы наглядно понимать, как выглядят пересечения и объединения множеств. Это поможет вам лучше запомнить алгоритм решения задач.

Использование программных средств для построения кругов Эйлера может ускорить процесс решения задач. Найдите подходящие инструменты, чтобы сделать решение более удобным и точным.

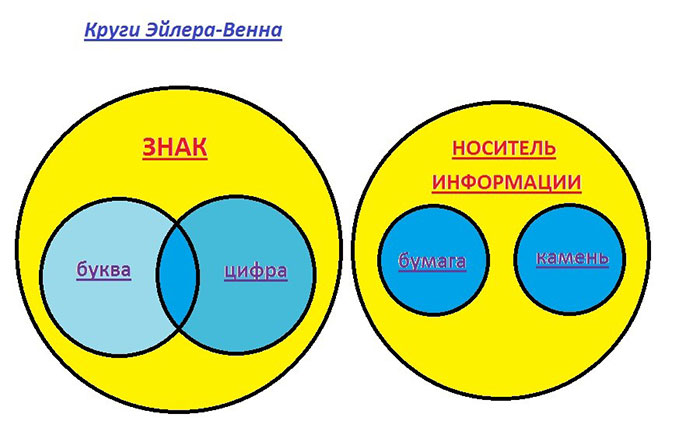
Не забывайте о важности точности в отображении множеств на диаграммах. Ошибки в расположении кругов могут привести к неверным выводам.

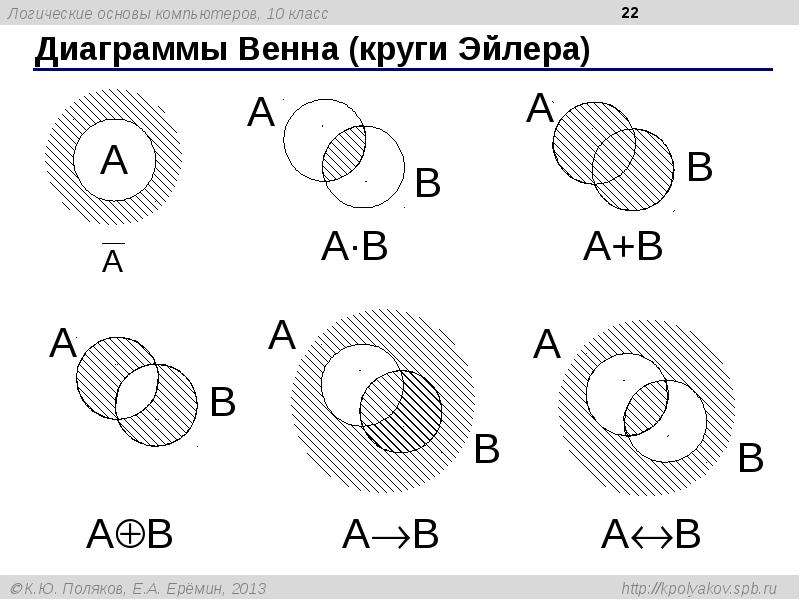
Регулярно проверяйте свои решения с помощью различных методов и подходов. Это поможет избежать ошибок и улучшит ваши навыки в области алгебры логики.

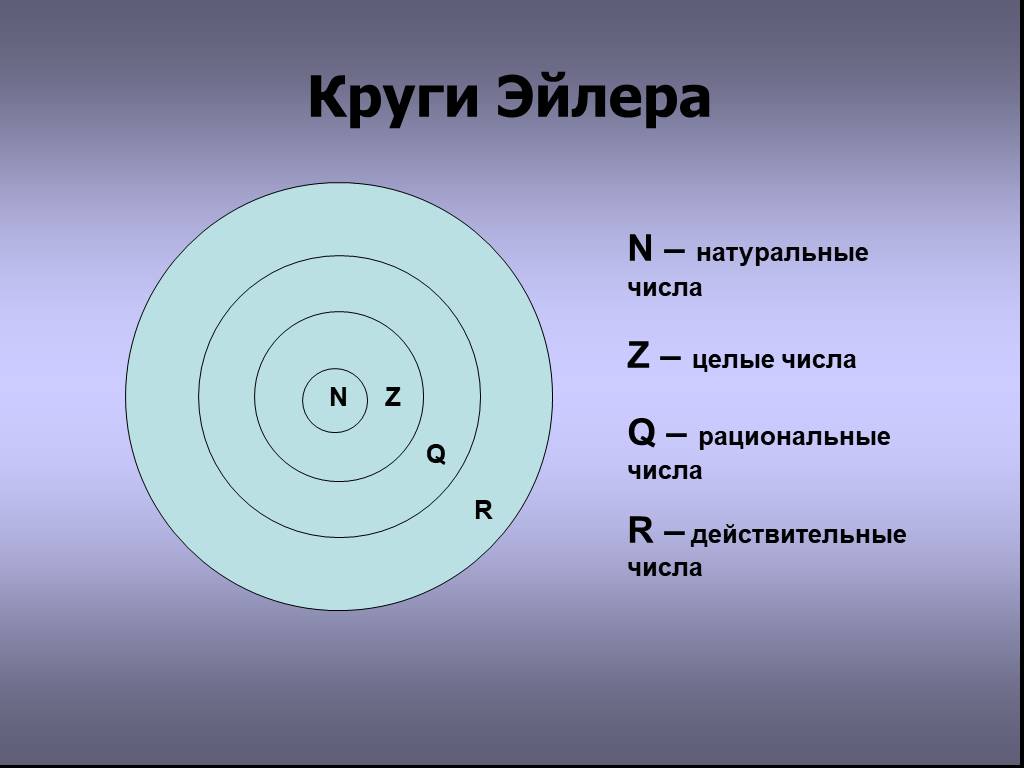
Практикуйтесь на задачах с несколькими множествами. Чем больше множеств, тем сложнее становится задача, и тем ценнее будет ваш опыт в использовании кругов Эйлера.

Не забывайте, что круги Эйлера — это только один из методов решения логических задач. Попробуйте комбинировать их с другими методами, чтобы достичь оптимальных результатов.