Как правильно понимать и применять два круга Эйлера в математике и логике
На этой странице вы найдете полное объяснение двух кругов Эйлера, их визуализацию и примеры применения. Мы разберем, как можно использовать эти круги для решения логических задач, а также как их применять в различных областях математики и науки.
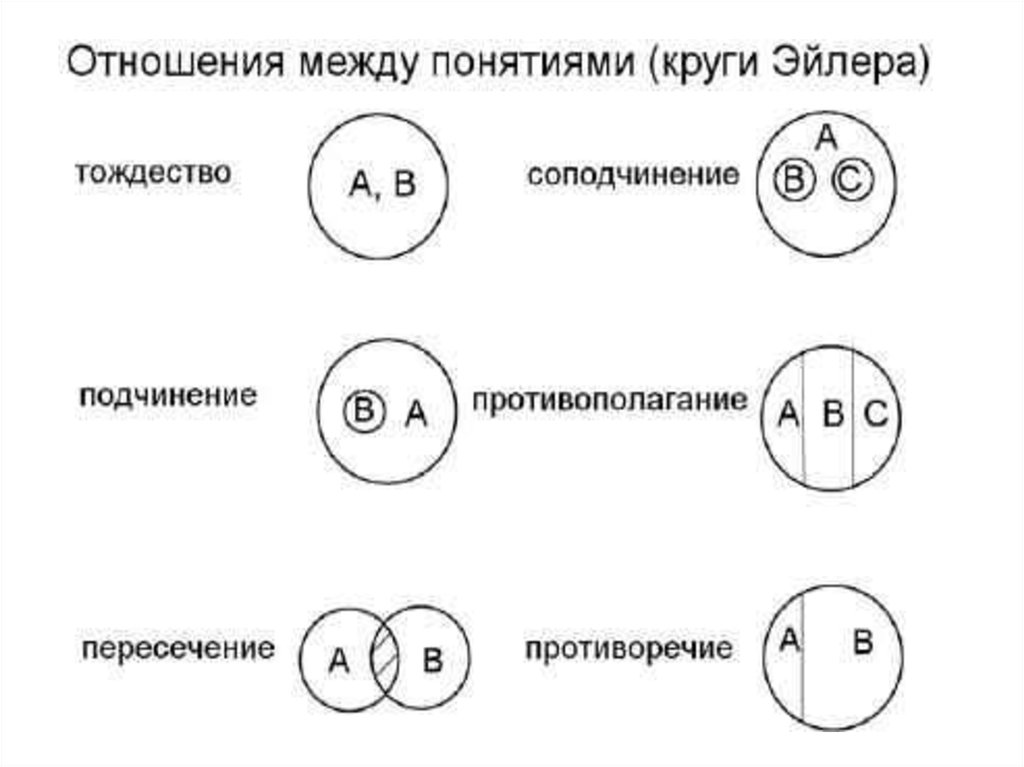

Для лучшего понимания концепции двух кругов Эйлера важно визуализировать их с помощью схем, чтобы наглядно увидеть пересечения и отношения между множествами.

Круги Эйлера. Логическая задача на множества. Иностранные языки

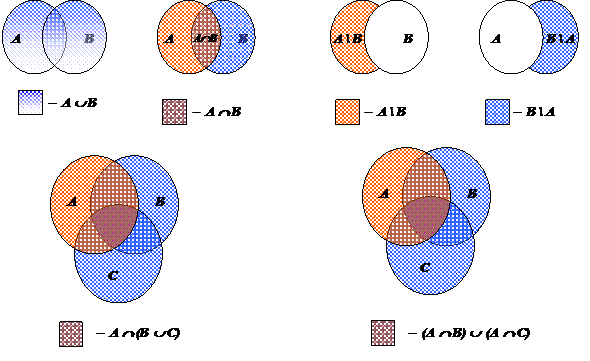
При решении задач с использованием кругов Эйлера всегда внимательно следите за правильностью логических операций при определении пересечений и объединений множеств.

Круги Эйлера за 3 минуты - ОГЭ по информатике 2024
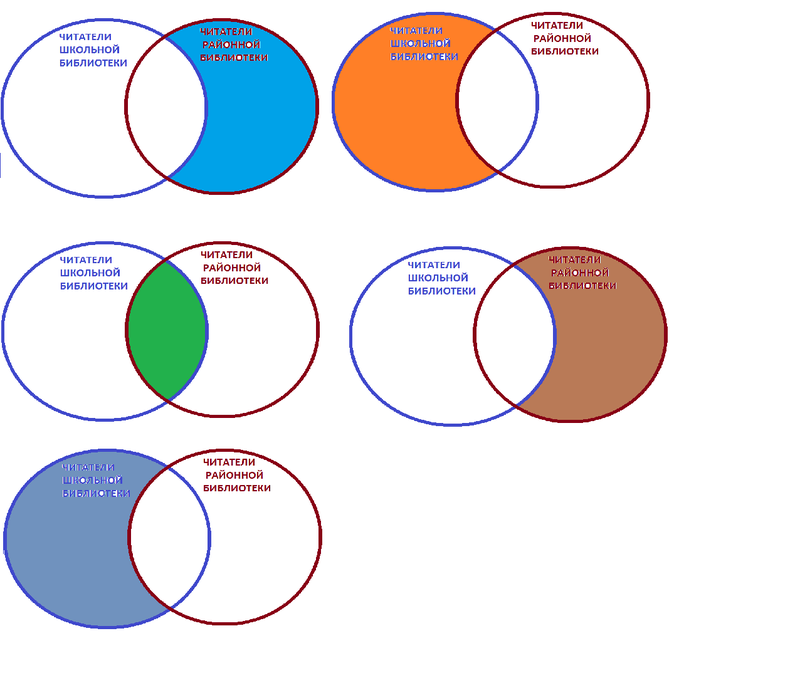
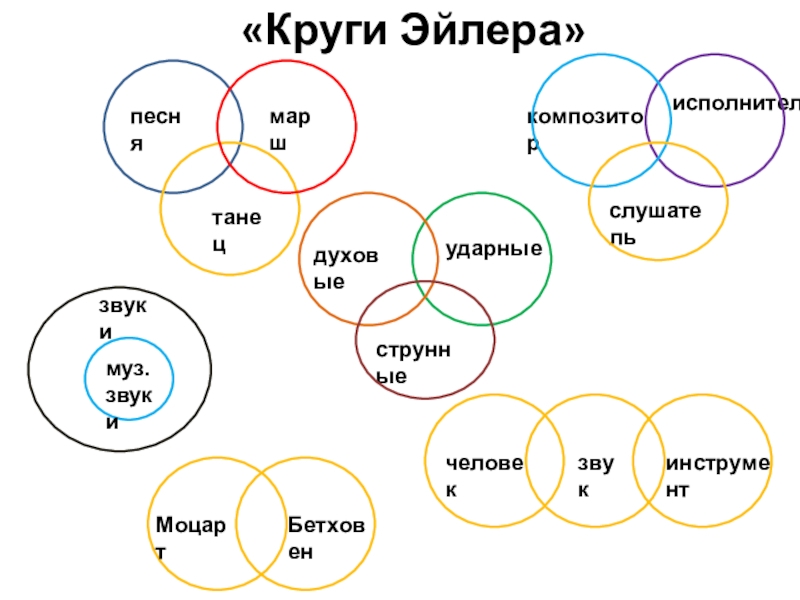
Не забывайте, что круги Эйлера можно использовать не только в математике, но и в других областях, например, в теории вероятностей или философии.
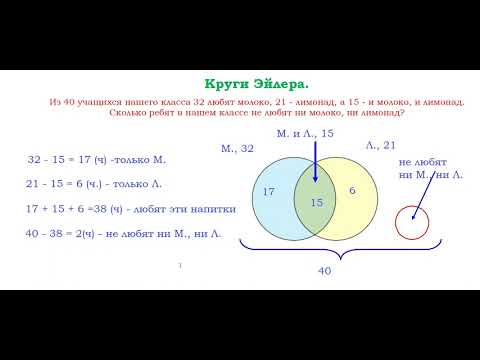
Круги Эйлера. Урок 2.
Для лучшего понимания рекомендую решить несколько практических задач, используя два круга Эйлера, чтобы закрепить теоретические знания на практике.

Задача об упаковке шаров – задача столетия, гипотеза Кеплера, «Нобель» по математике // Vital Math

Начинайте с простых примеров, постепенно переходя к более сложным, чтобы понять, как изменение условий влияет на пересечения множеств.

✅ Dwar/Двар - Рождественская Ель - Небесное усиление или Союз созвездий


Помните, что правильное отображение кругов Эйлера на бумаге помогает избежать ошибок в расчетах и логических выводах.
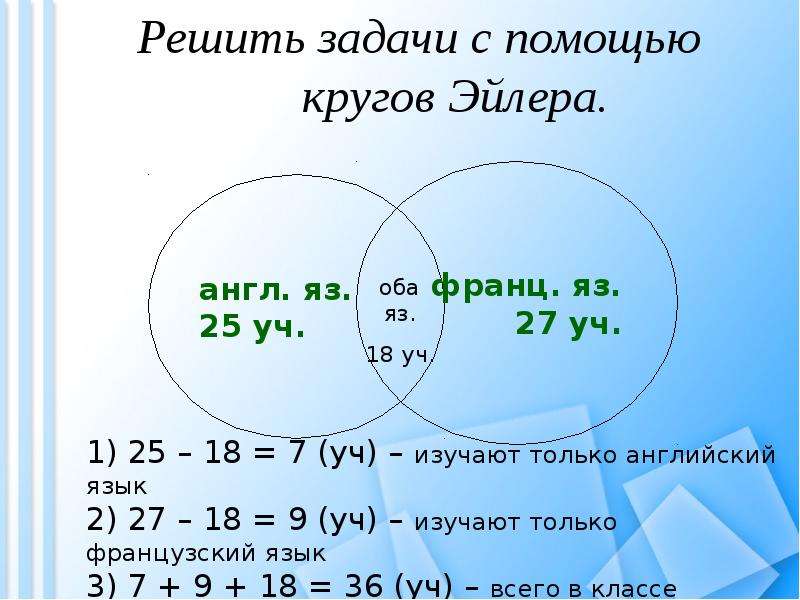
Используйте разные цвета или штриховки для обозначения различных областей кругов Эйлера, чтобы лучше различать части множества.
ЭЙЛЕР. Грандиозное математическое наследие
Важно учитывать, что два круга Эйлера могут описывать как отношения между двумя множествами, так и более сложные взаимодействия в контексте многократных пересечений.

Самый короткий тест на интеллект Задача Массачусетского профессора

Для более глубокого понимания можно изучить примеры из реальной жизни, где используется аналогичная логика, например, в анализе данных или в принятии решений.


Не забывайте, что круги Эйлера — это мощный инструмент для визуализации взаимосвязей и упрощения сложных логических задач.

Круги Эйлера в реальной жизни. Математика на QWERTY