Пошаговый разбор уравнений с функцией tg(x)
На этой странице вы найдете полезные советы и фотографии, которые помогут разобраться с решением уравнений, содержащих тангенс, и освоить основные методы работы с ними.



Перед началом решения уравнения tg(x) = A определите область допустимых значений.

Простейшее тригонометрическое уравнение tgx=a


Помните, что функция тангенса периодическая с периодом π, что важно учитывать при записи общего решения.
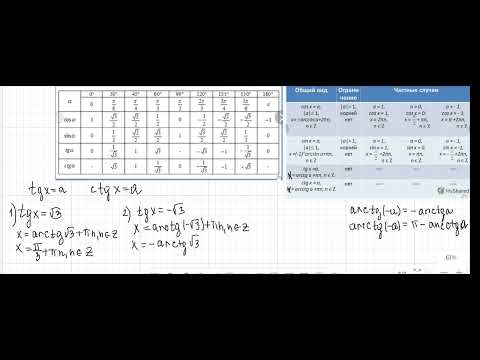
Решение уравнений вида tgx=a и ctgx=a

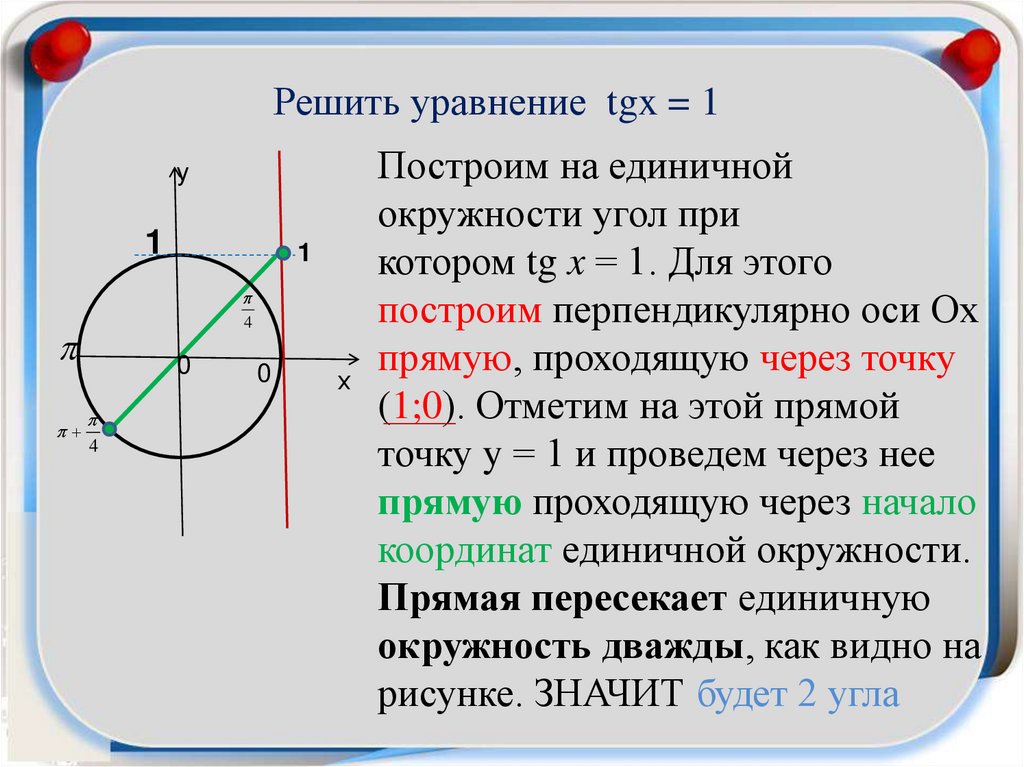
Убедитесь, что знаменатель не равен нулю, если тангенс представлен в виде дроби.

Решение уравнений вида tg x = a и ctg x = a

Если значение A выходит за пределы области значений тангенса, то уравнение не имеет решений.
Устная задача с собеседования в МФТИ


Используйте основное тригонометрическое тождество для упрощения сложных уравнений.
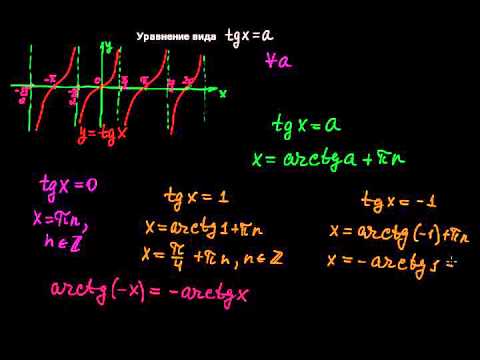
§161 Уравнения вида tg x=a

Решая tg(x) = A, запишите общее решение: x = arctg(A) + πn, где n — любое целое число.
Для проверки правильности решения подставьте найденные значения x в исходное уравнение.

10 класс. Решение уравнений tg x =a
Внимательно следите за единицами измерения углов: градусы или радианы.
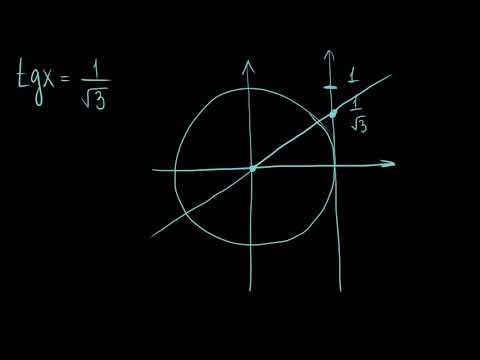
Как решать tgx=a
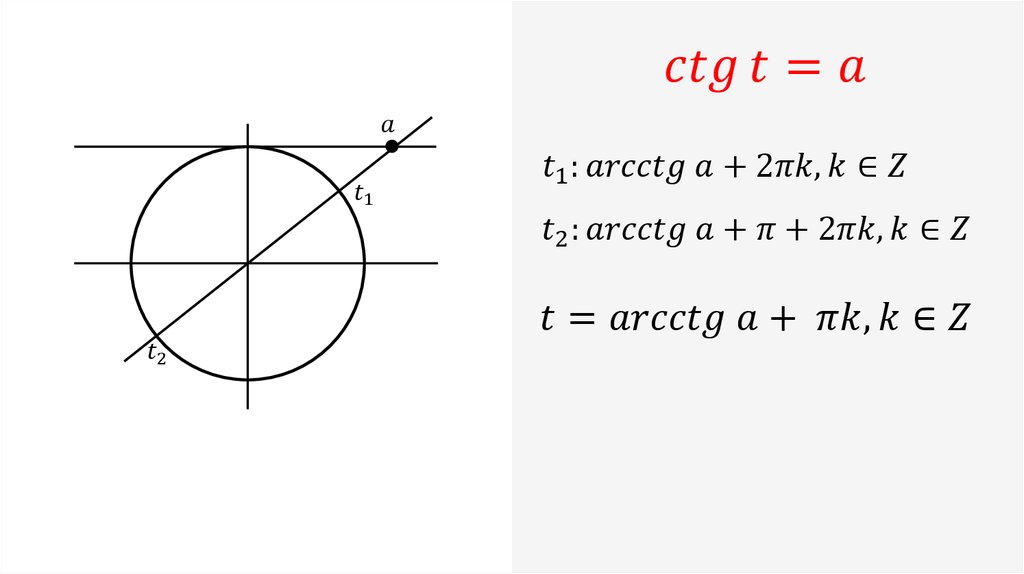

Используйте графики функций, чтобы визуализировать решение уравнения.

Если уравнение сложное, разбейте его на несколько более простых частей и решайте поэтапно.

Решение тригонометрических уравнений (тангенс) . tg x = a