Как построить уравнение секущей прямой для функции: пошаговое руководство
Уравнение секущей к графику функции помогает исследовать поведение функции в окрестности конкретных точек. Секущая линия пересекает график функции в двух различных точках, и её уравнение важно для анализа изменений функции, нахождения производной и понимания касательных. В этой статье представлены полезные советы по нахождению уравнения секущей линии и его применению на практике.
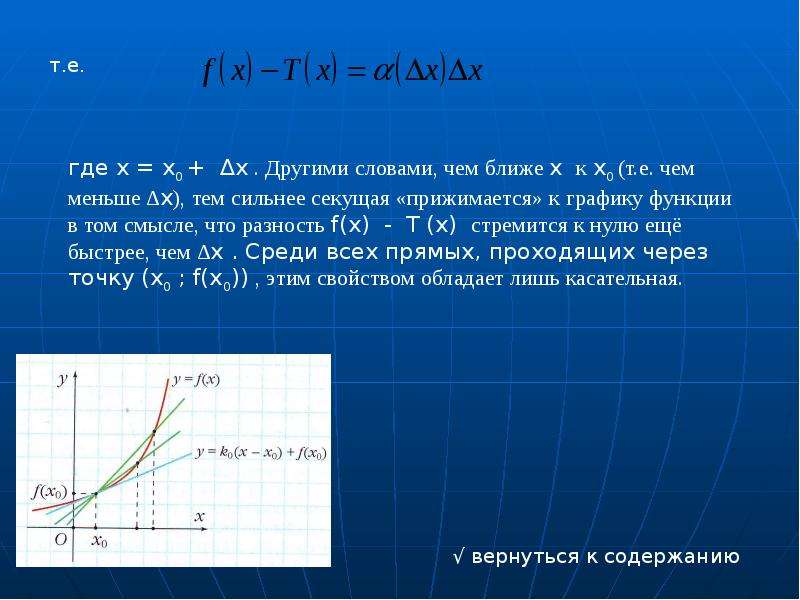
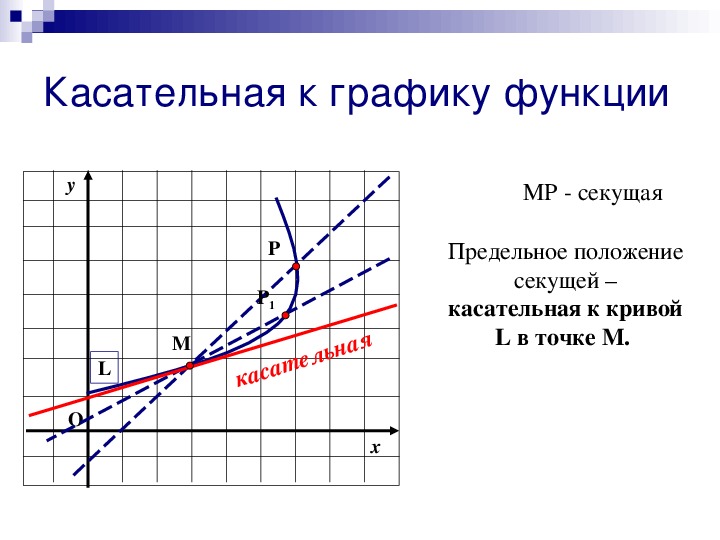
Для нахождения уравнения секущей линии выберите две точки на графике функции, через которые будет проходить секущая.
Касательная к графику функции в точке. 10 класс.
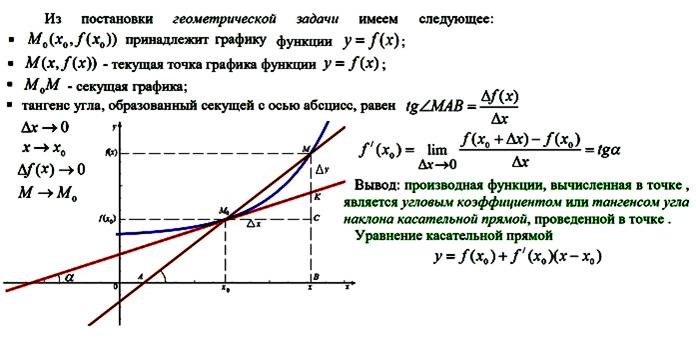
Используйте формулу углового коэффициента: m = (f(x2) - f(x1)) / (x2 - x1), где x1 и x2 — это абсциссы выбранных точек.

Уравнение нормали и касательной к графику функции: Математический анализ для Data Science
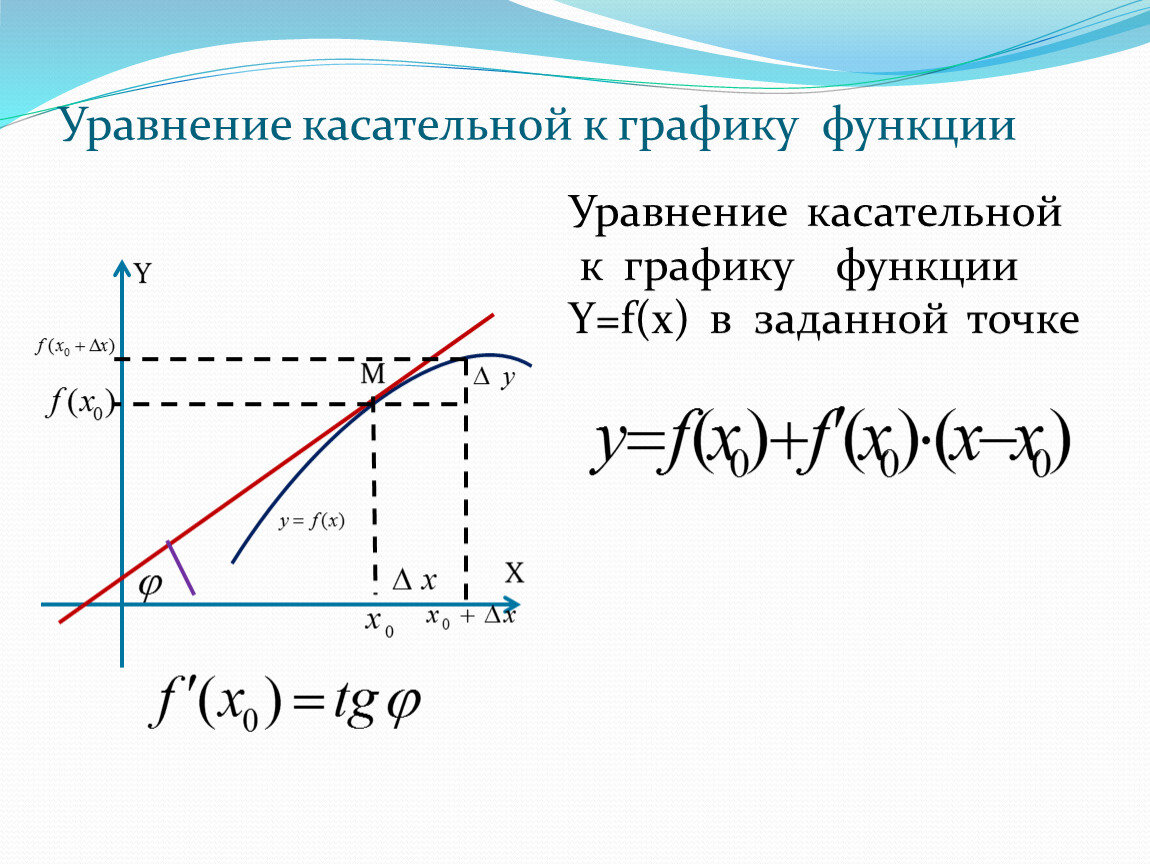
После нахождения углового коэффициента подставьте его в уравнение прямой в виде y - y1 = m(x - x1), где (x1, y1) — это одна из точек секущей.

Уравнение касательной

Помните, что для точности необходимо работать с координатами точек, которые точно лежат на графике функции.

Уравнение касательной к графику функции - Алгебра 10 класс #45 - Инфоурок
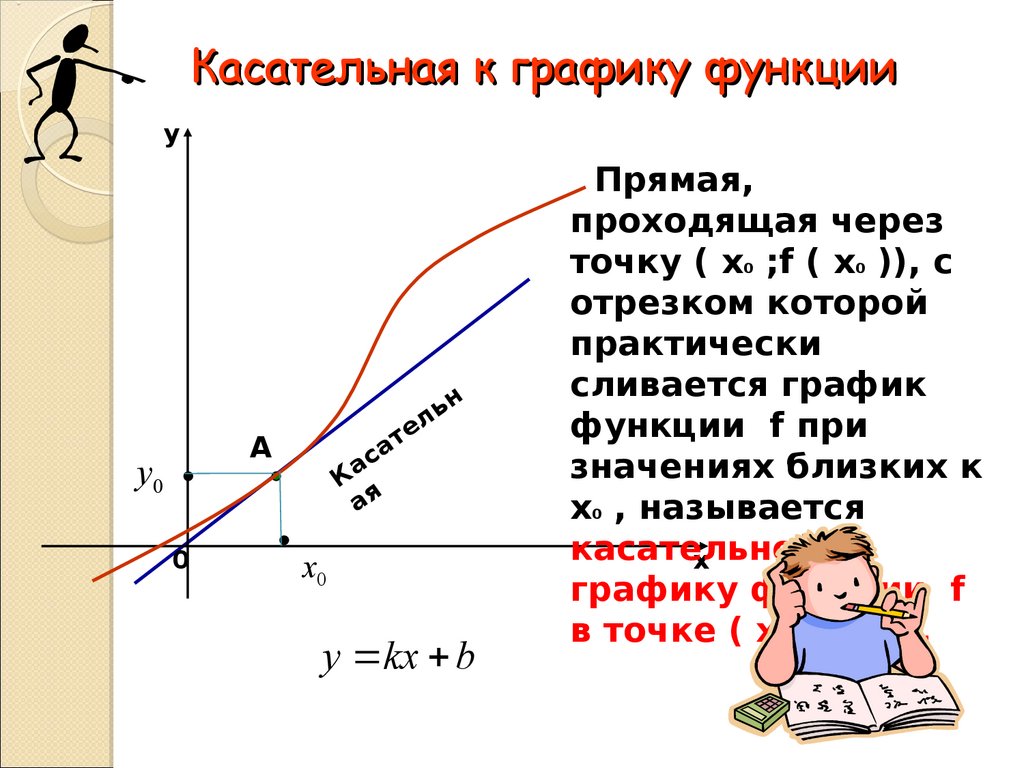
Не забывайте, что секущая линия приближает поведение функции в окрестности выбранных точек, но не всегда точно отражает её форму.
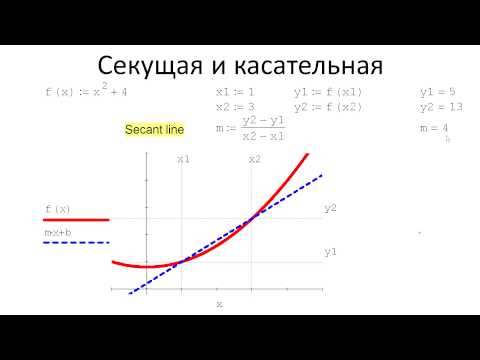
0102. Графики на плоскости: секущая и касательная
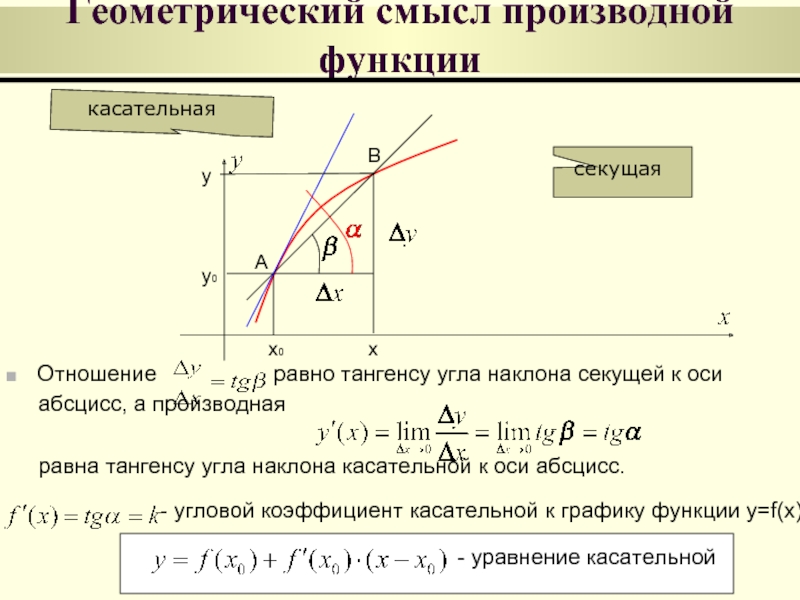
Если вам нужно построить несколько секущих, меняйте позиции точек и пересчитывайте угловой коэффициент.
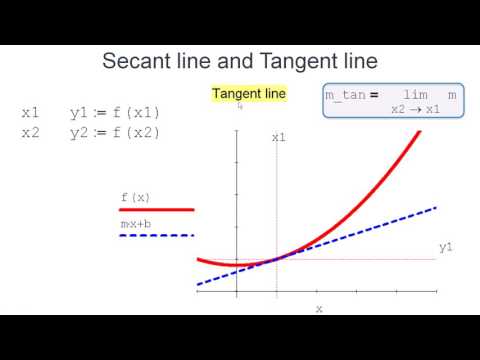
Секущая и Касательная
Для вычисления производной функции с помощью секущей линии можно использовать предел углового коэффициента при стремлении разности координат точек к нулю.

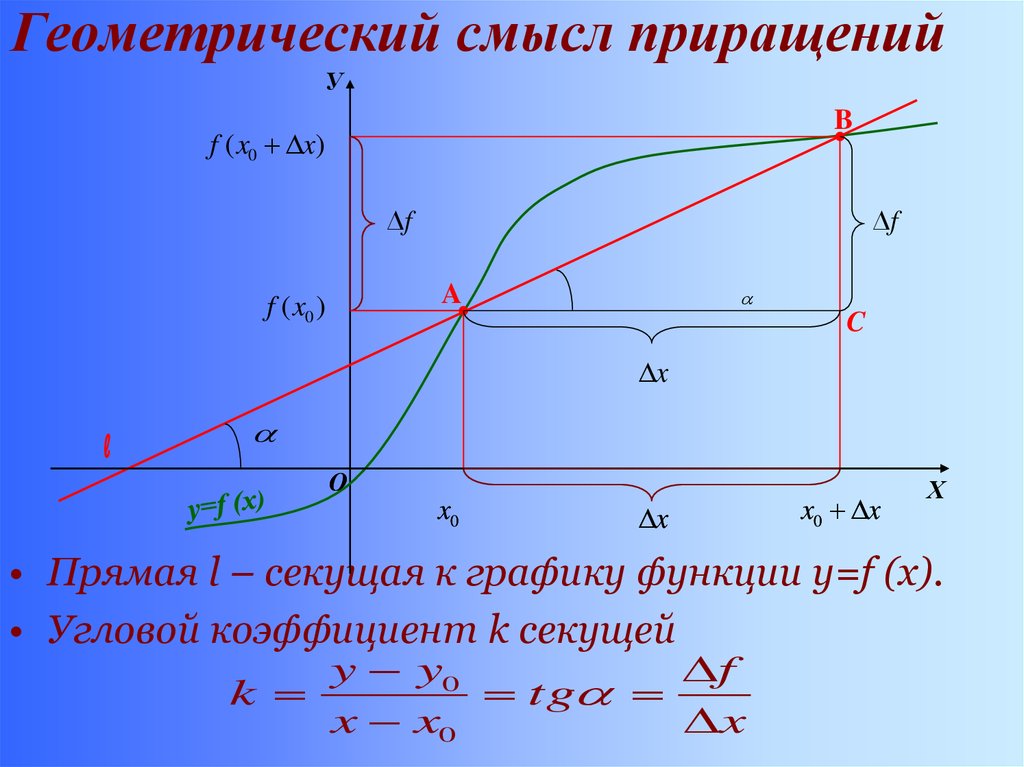
При приближении точек друг к другу угловой коэффициент секущей будет стремиться к значению производной функции в этой точке.

Геометрический смысл производной - Касательная

УРАВНЕНИЕ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ #maths #derivatives
В случае с нелинейными функциями секущие линии могут давать разные угловые коэффициенты в разных точках, что помогает понять изменения функции.

Тщательно проверяйте расчёты углового коэффициента и точность подставляемых координат, чтобы избежать ошибок в построении секущей линии.
