Треугольник Паскаля: от теории до пятого уровня
Треугольник Паскаля — это математическая конструкция, представляющая собой треугольную таблицу биномиальных коэффициентов. На этой странице собраны полезные советы и наглядные фотографии для изучения первых пяти рядов.


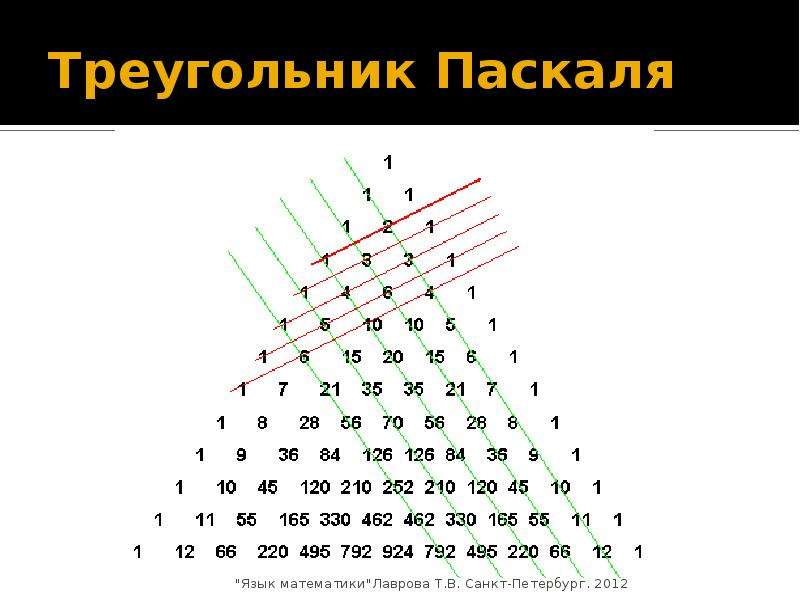
Начните с понимания принципа построения треугольника: каждая ячейка является суммой двух элементов выше.

Числа сочетаний. Треугольник Паскаля - Ботай со мной #059 - Борис Трушин -
Обратите внимание на симметрию треугольника: элементы зеркально отображаются относительно центральной оси.

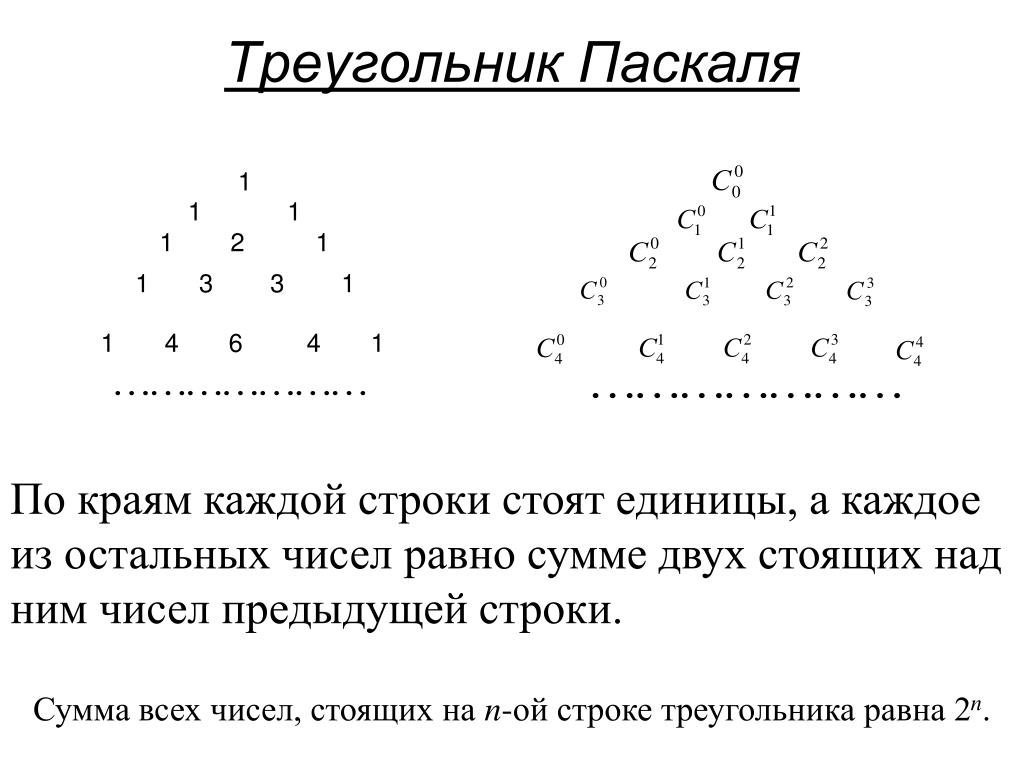
Треугольник Паскаля

Изучите первый и последний элементы каждого ряда: они всегда равны единице.

5 Треугольник Паскаля по модулю два
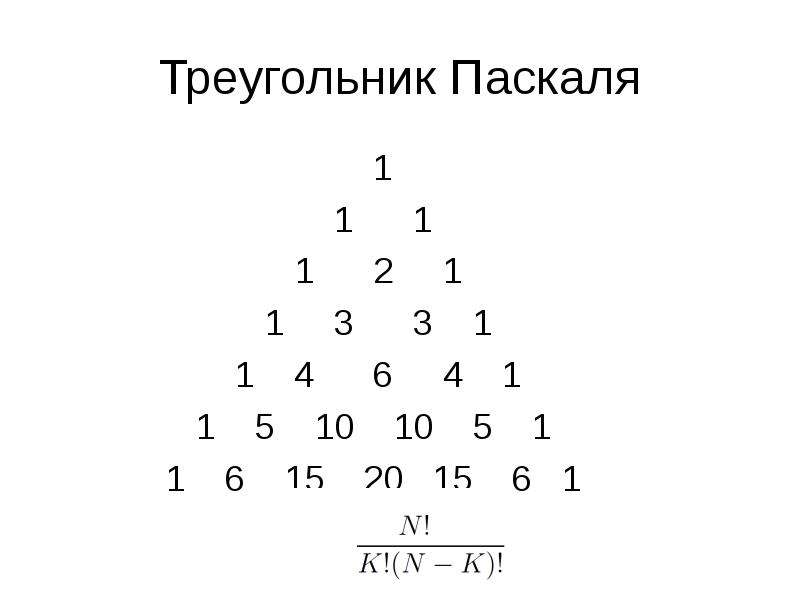
Попробуйте найти закономерность в числе элементов в каждом ряду: их количество равно номеру ряда плюс один.

Число Бога. Неопровержимое доказательство Бога; The number of God. The incontrovertible proof of God

Используйте треугольник для нахождения биномиальных коэффициентов в разложении (a + b)^n.

Полный Коран в исполнении Мишари Рашид Аль-Афаси 3-1

Рассмотрите связь треугольника Паскаля с числами Фибоначчи: сумма диагоналей связана с этим числовым рядом.

Удивительный треугольник Паскаля - Лекции по математике – Яков Ерусалимский - Научпоп - НаукаPRO
Обратите внимание на центральные элементы четных рядов: они дают информацию о комбинациях.
Попробуйте самостоятельно построить треугольник до пятого ряда, чтобы лучше усвоить принцип.

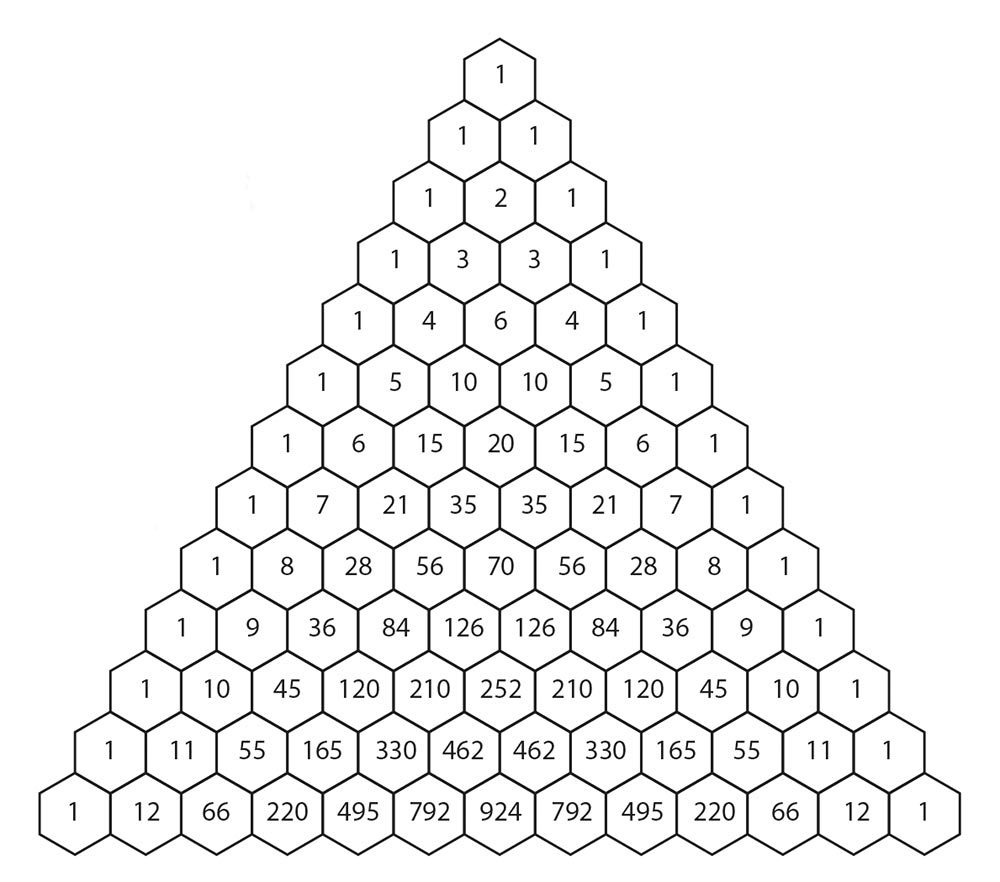
Треугольник Паскаля
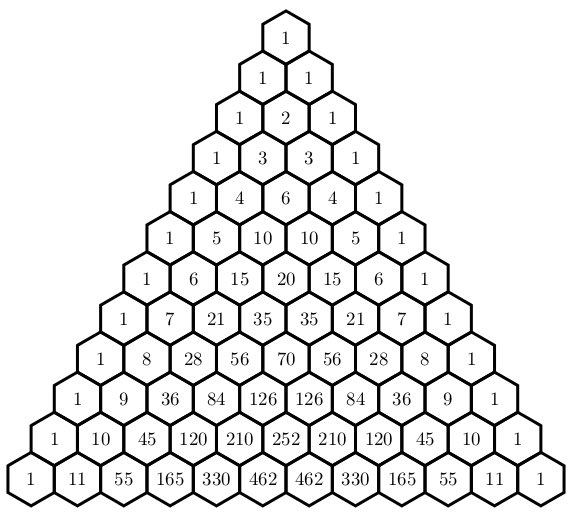

Используйте цветовую маркировку для выделения разных рядов и понимания закономерностей.

Как из треугольника Паскаля сделать ковёр Серпинского?

Запомните, что треугольник Паскаля помогает решать задачи по комбинаторике и теории вероятностей.

Бином Ньютона и треугольник Паскаля - Учитель года Москвы — 2020

Зачем нужен треугольник Паскаля (спойлер: для формул сокращённого умножения)