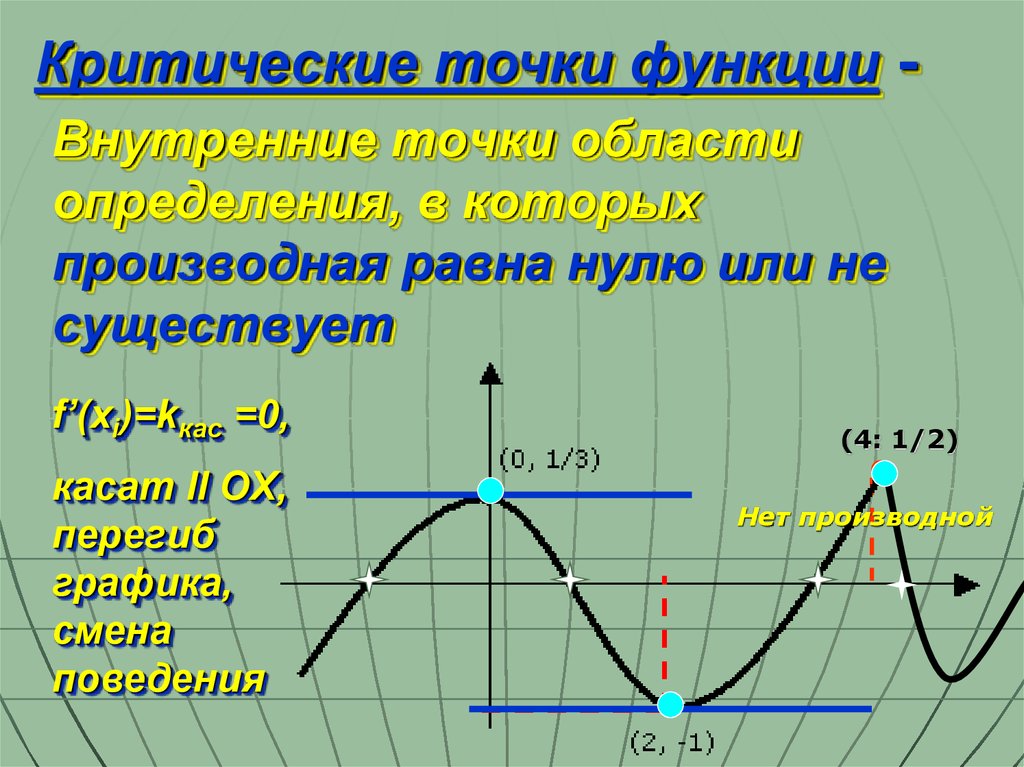
Разбор точек с нулевой производной функции: советы и примеры
В этой статье вы найдете объяснение, как определить точки, в которых производная функции равна нулю, а также практические советы для их вычисления и анализа. Подборка фото и иллюстраций поможет лучше понять тему.
Перед поиском точек нулевой производной найдите область определения функции.
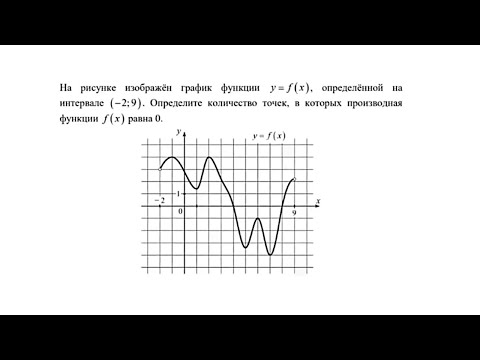
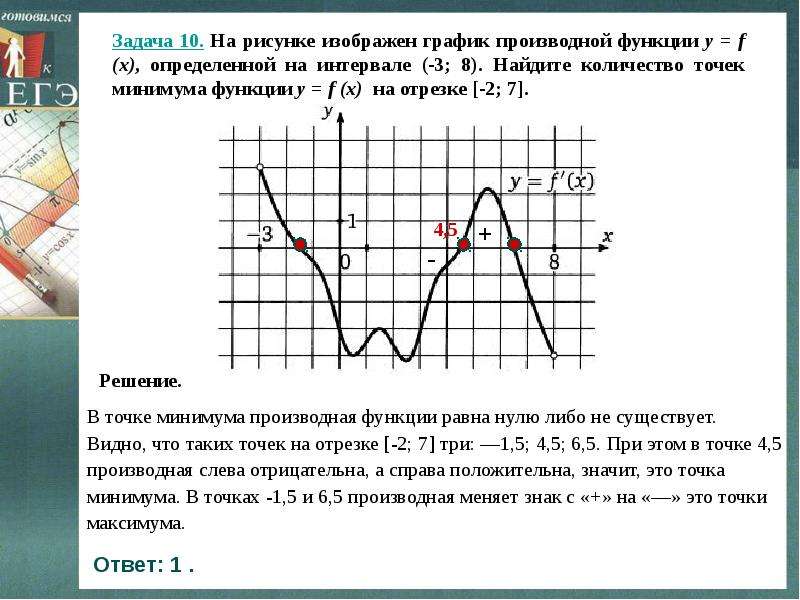
Задание 4, найти точки в которых производная функции равна нулю
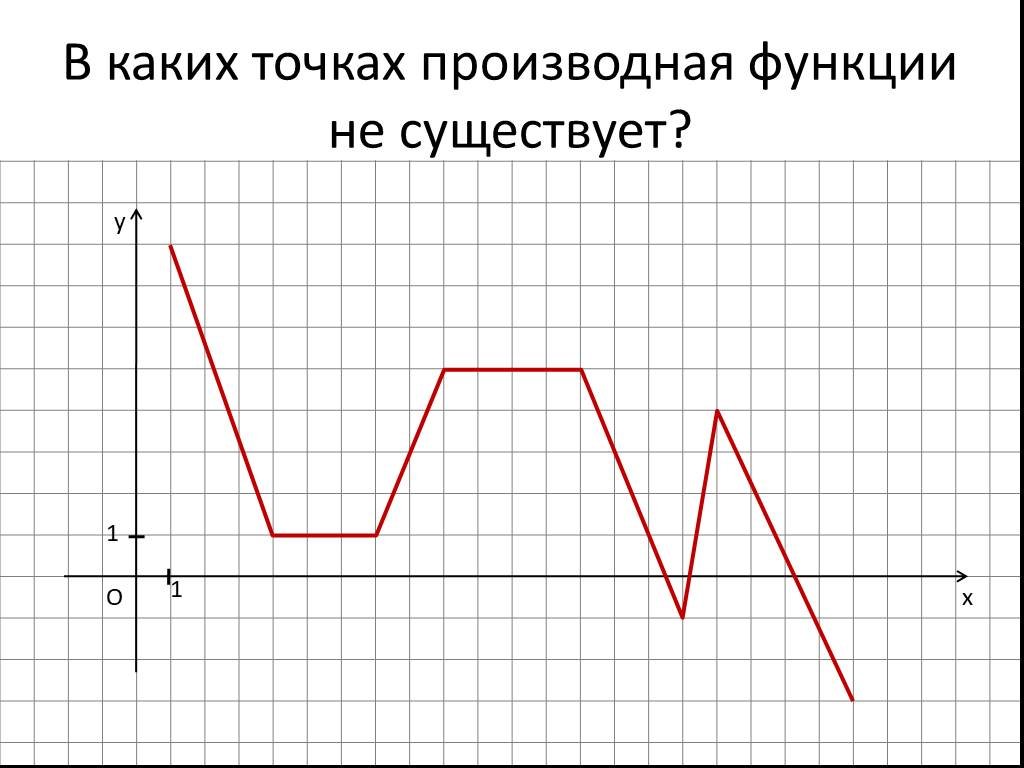
Выполните дифференцирование функции, чтобы получить её производную.

Общая схема исследования функции и построение ее графика
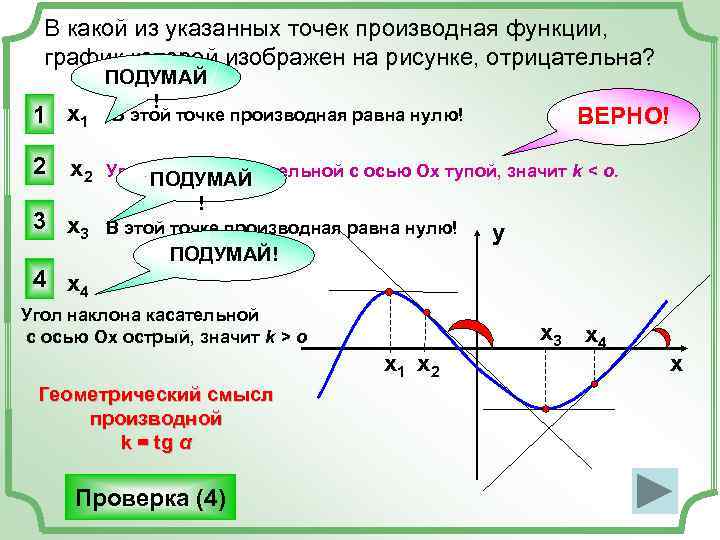
Приравняйте производную к нулю и решите полученное уравнение для нахождения критических точек.

4. Вычисление производных примеры. Самое начало.
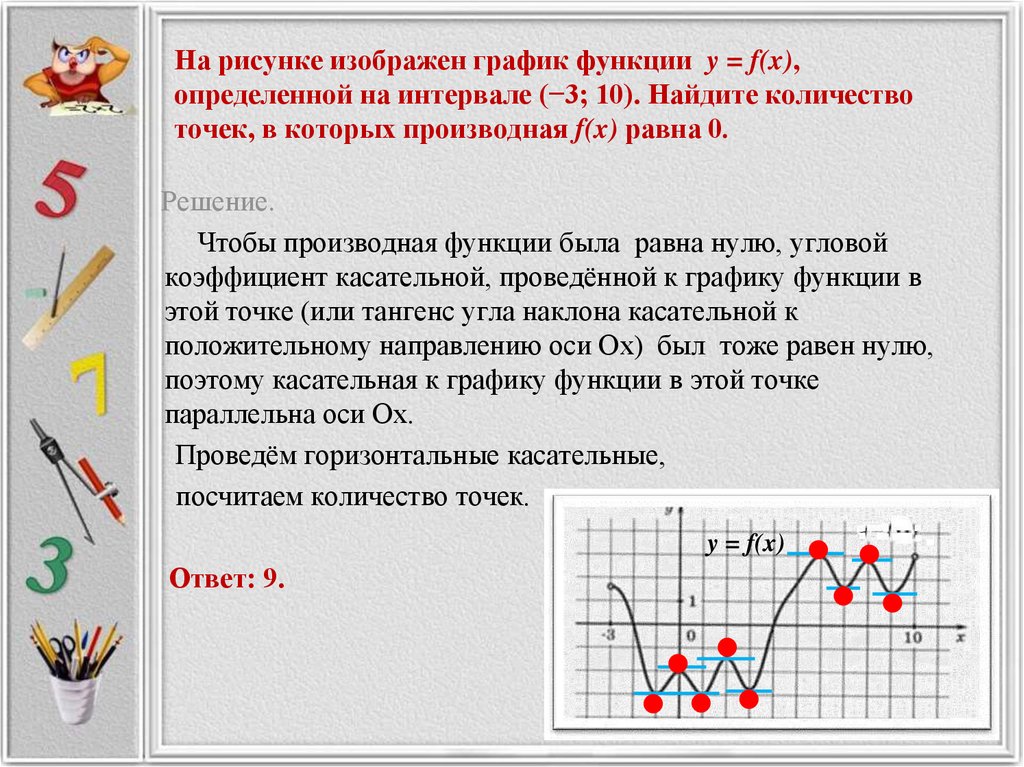
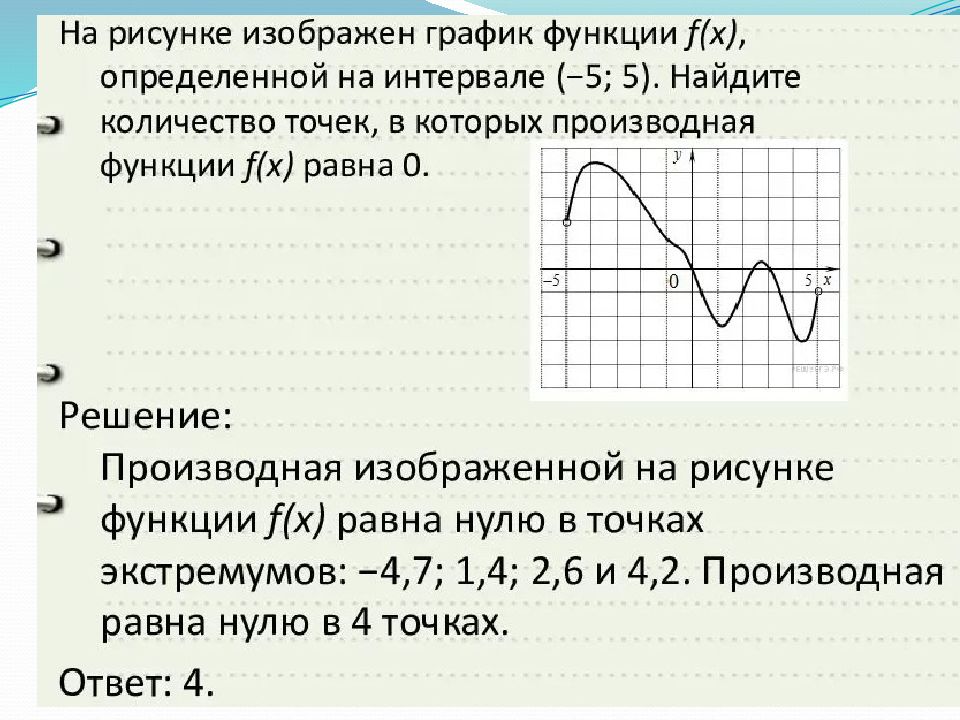
Проверьте каждую найденную точку на принадлежность области определения функции.

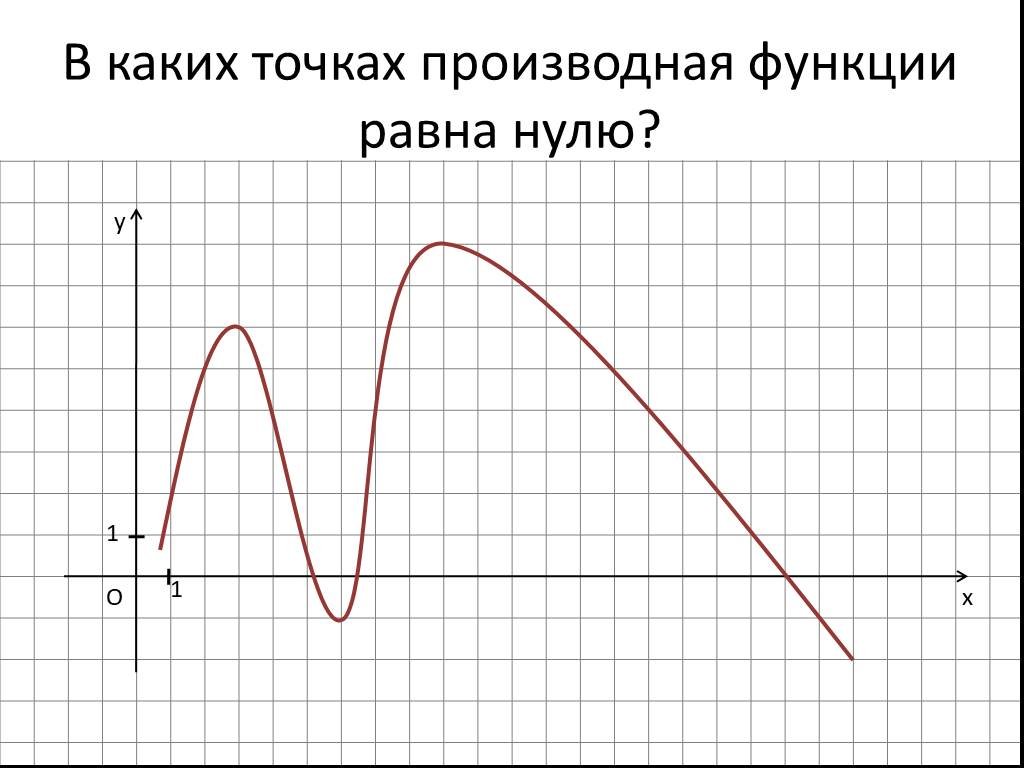
Как найти нули функции? #shorts
Используйте второй производной или метод анализа знаков для проверки характера критических точек (минимум, максимум, перегиб).

Консультация к коллоквиуму по квантовой физике, Глазков В.Н., 07.12.2024
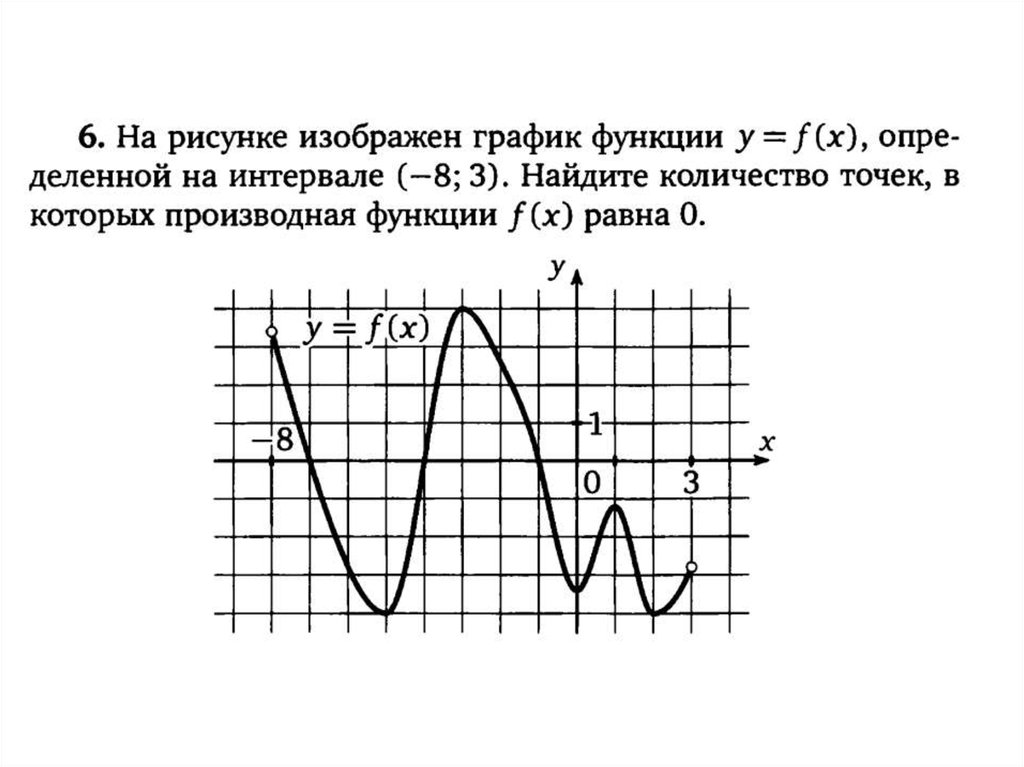
Для сложных функций рассмотрите использование численных методов нахождения нулей производной.
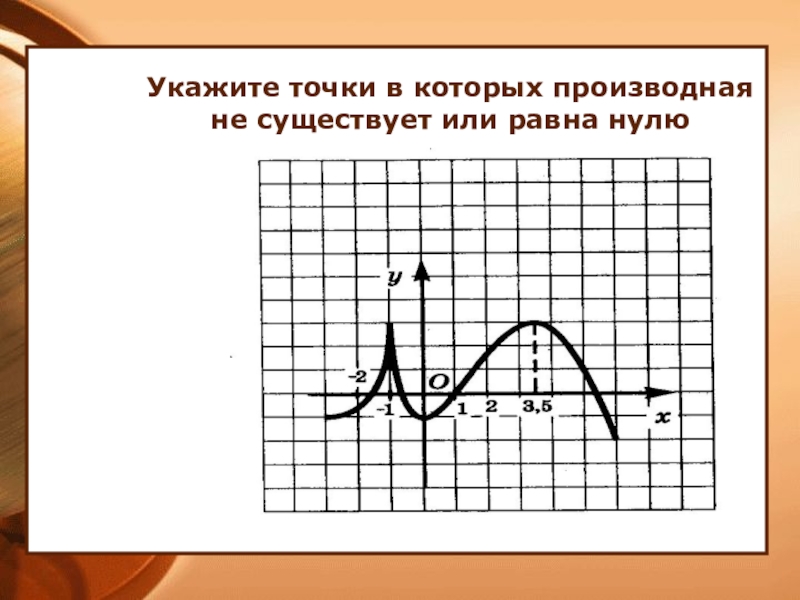
Не забывайте учитывать возможные ошибки в расчетах, особенно при работе с дробными или иррациональными выражениями.
Постройте график функции для визуального анализа её поведения в окрестности найденных точек.
Проверьте, могут ли точки с нулевой производной быть точками экстремума или перегиба.
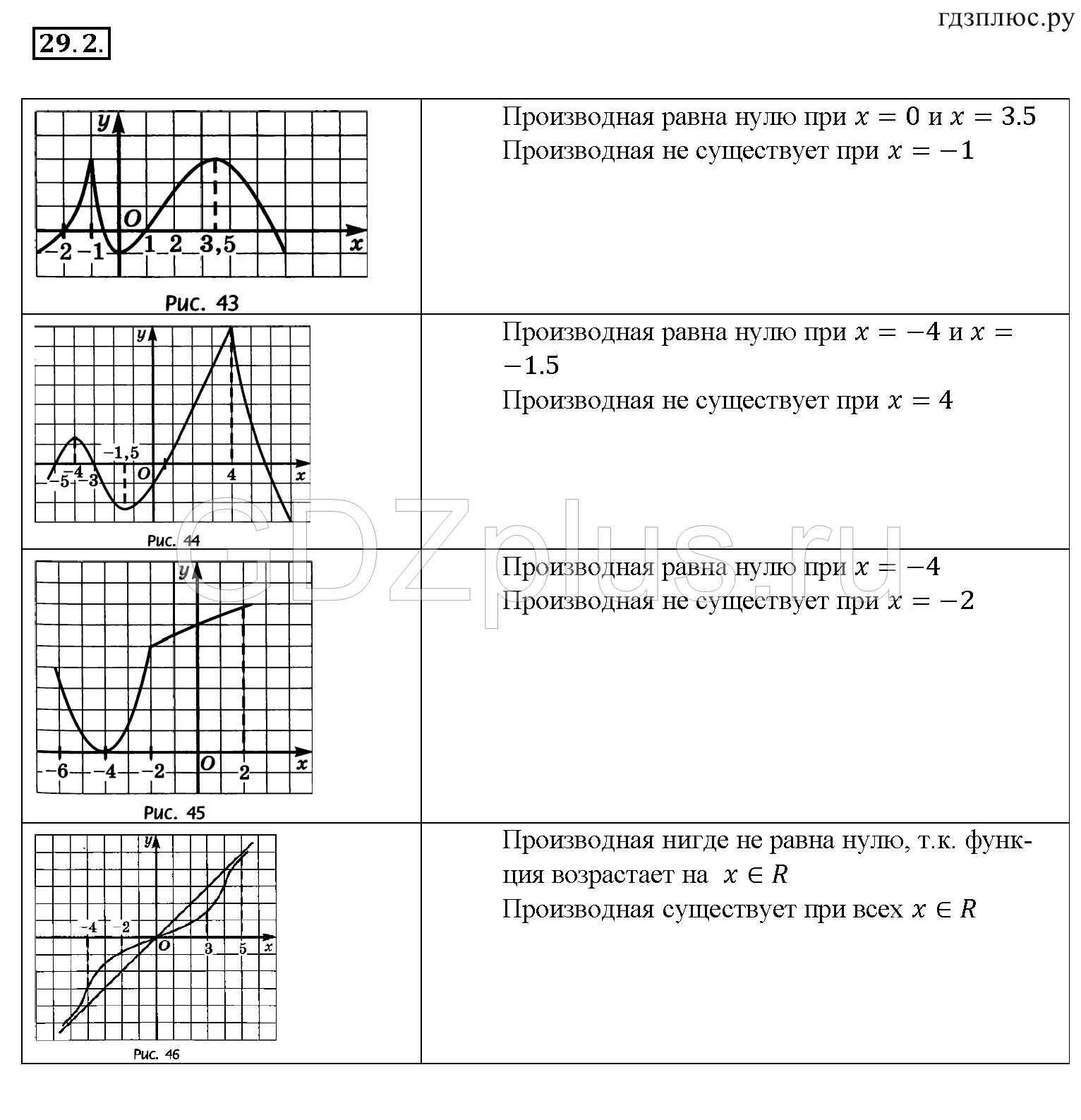
Убедитесь, что критические точки интерпретируются правильно в контексте задачи или приложения.
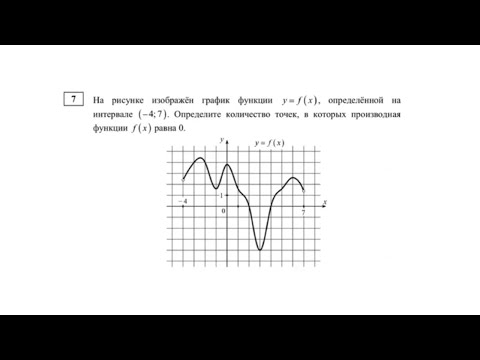
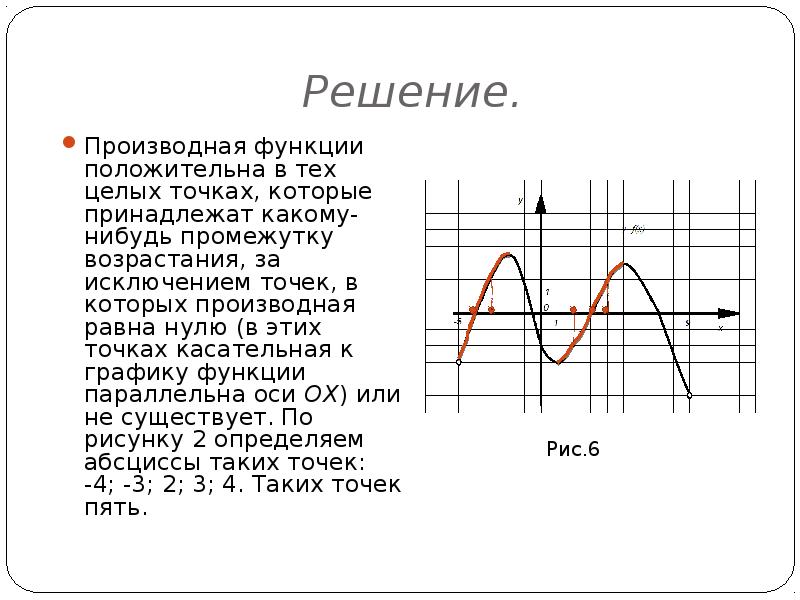
Задание 7, найти количество точек, в которых производная функции равна 0