Типы функций принадлежности и их роль в теории нечетких множеств
Функции принадлежности являются важной частью теории нечетких множеств. Они определяют степень принадлежности элементов множеству и играют ключевую роль в обработке нечеткой информации. В этом разделе мы рассмотрим различные типы функций принадлежности, их особенности и применение в задачах, связанных с нечеткой логикой.
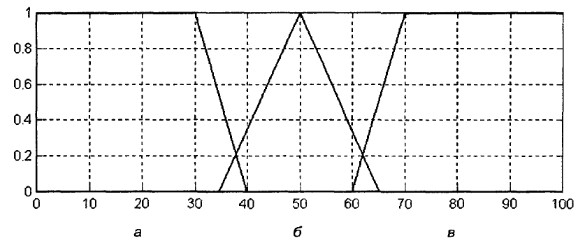

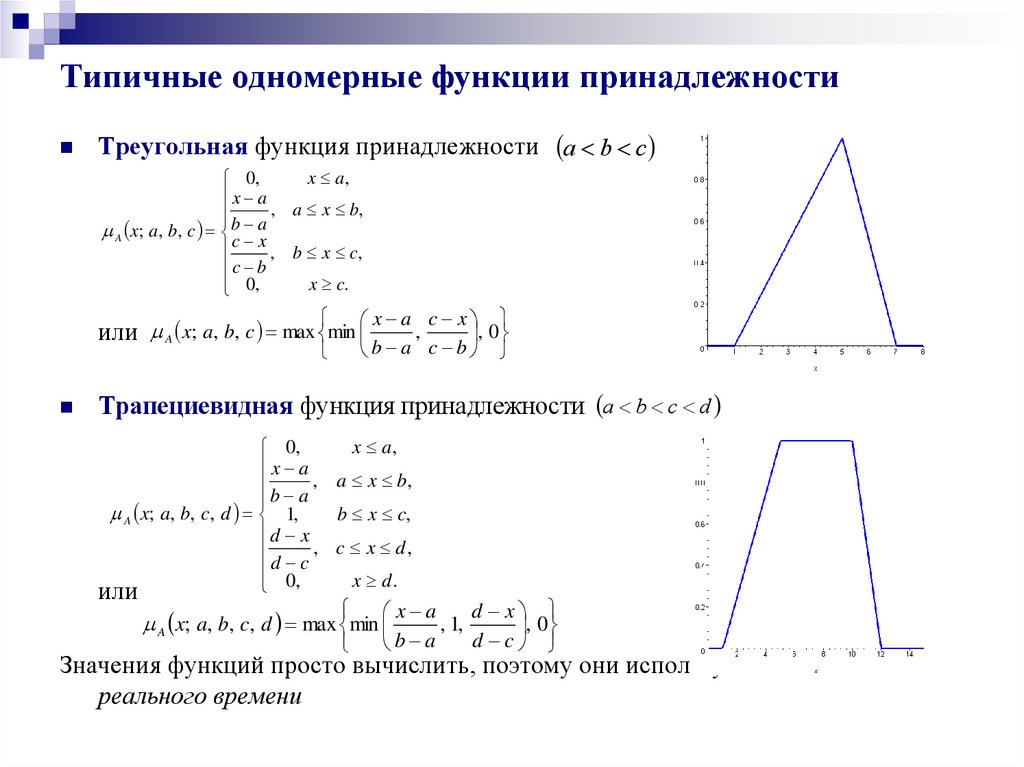
При выборе типа функции принадлежности для конкретной задачи важно учитывать степень неопределенности, с которой вы работаете. Некоторые типы функций подходят для более четких данных, а другие – для более неясных или размытых ситуаций.

Wolframalpha: аналитическое задание функций принадлежности нечётких множеств

Использование гладких функций принадлежности, например, гауссовых или треугольных, может помочь в моделировании ситуаций, где неопределенность должна быть представлена плавно и без резких изменений.

Чем различаются характеристическая функция и функция принадлежности? Душкин объяснит
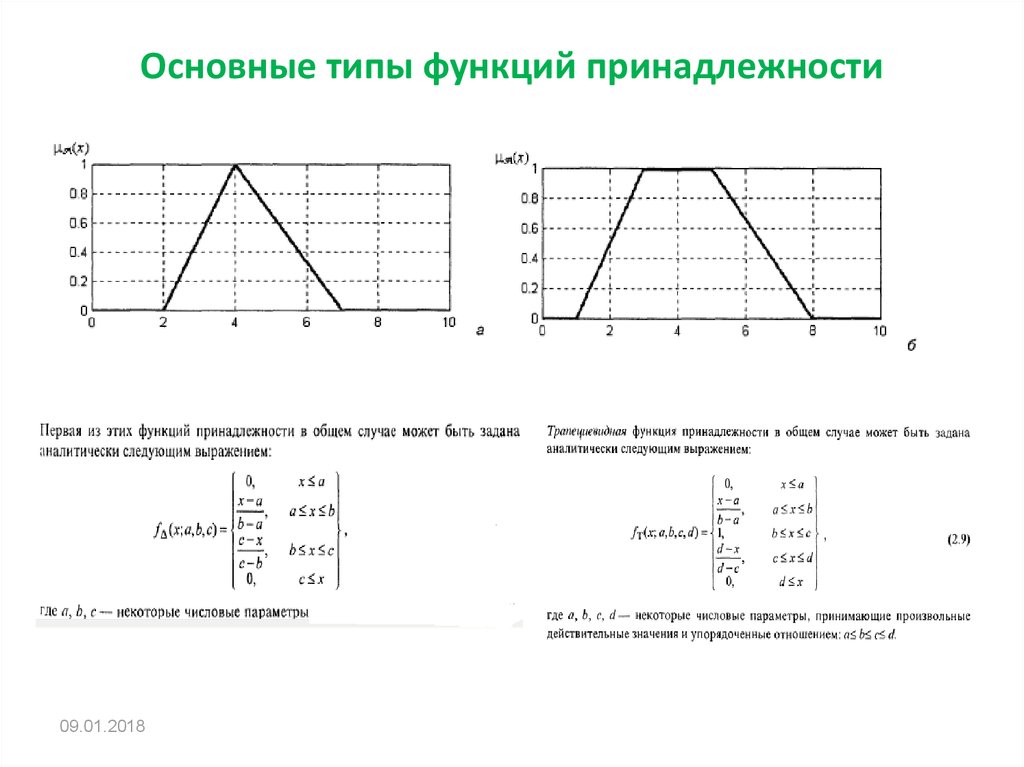

Для задач, где требуется четкое разделение на категории, могут подойти жесткие функции принадлежности, такие как ступенчатые функции.
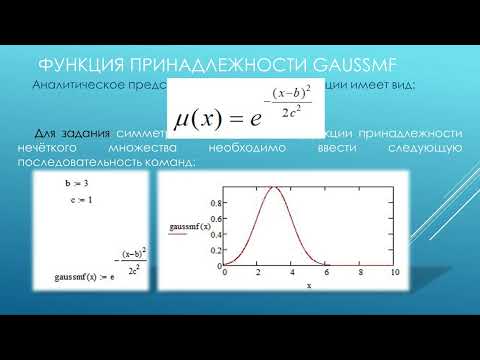
Построение в Mathcad функций принадлежности нечётких множеств
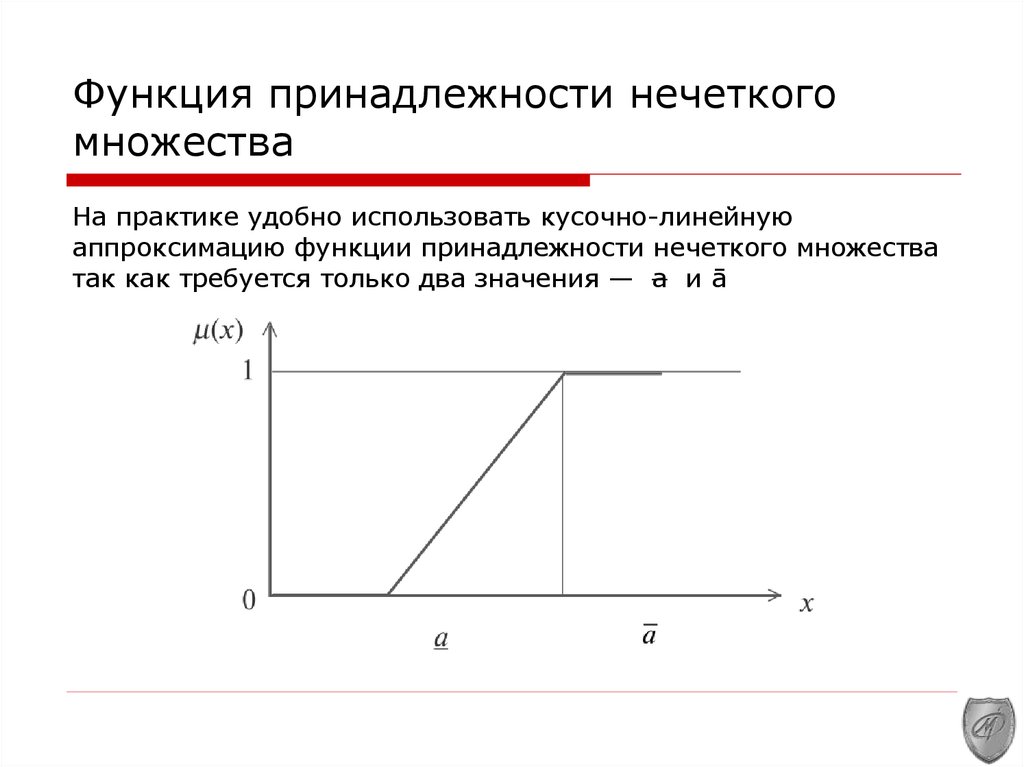
Важно помнить, что выбор функции принадлежности зависит от контекста: для описания феноменов с непрерывной природой лучше использовать гладкие функции, а для дискретных состояний — более жесткие.

Применение теории нечетких множеств к моделированию в экономике
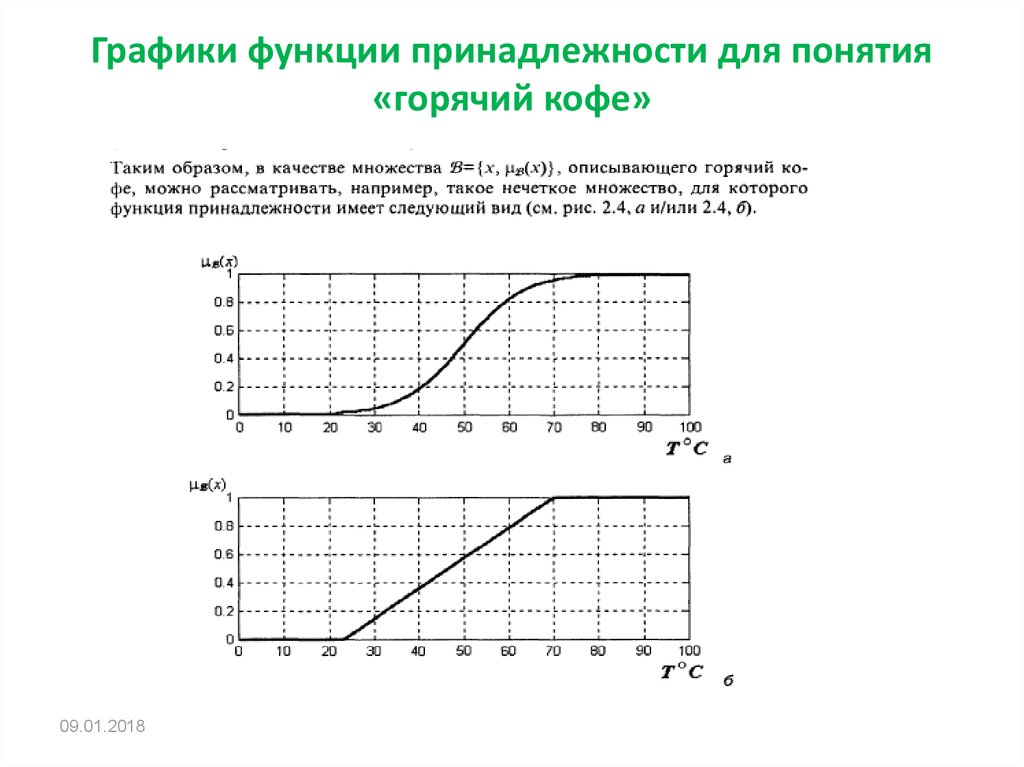
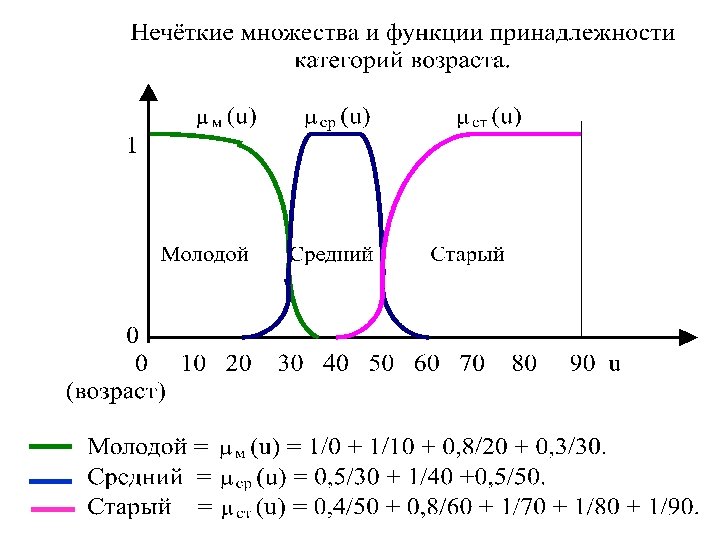
Использование комбинированных функций принадлежности может помочь более точно моделировать сложные системы с различными типами неопределенности.

лекция \
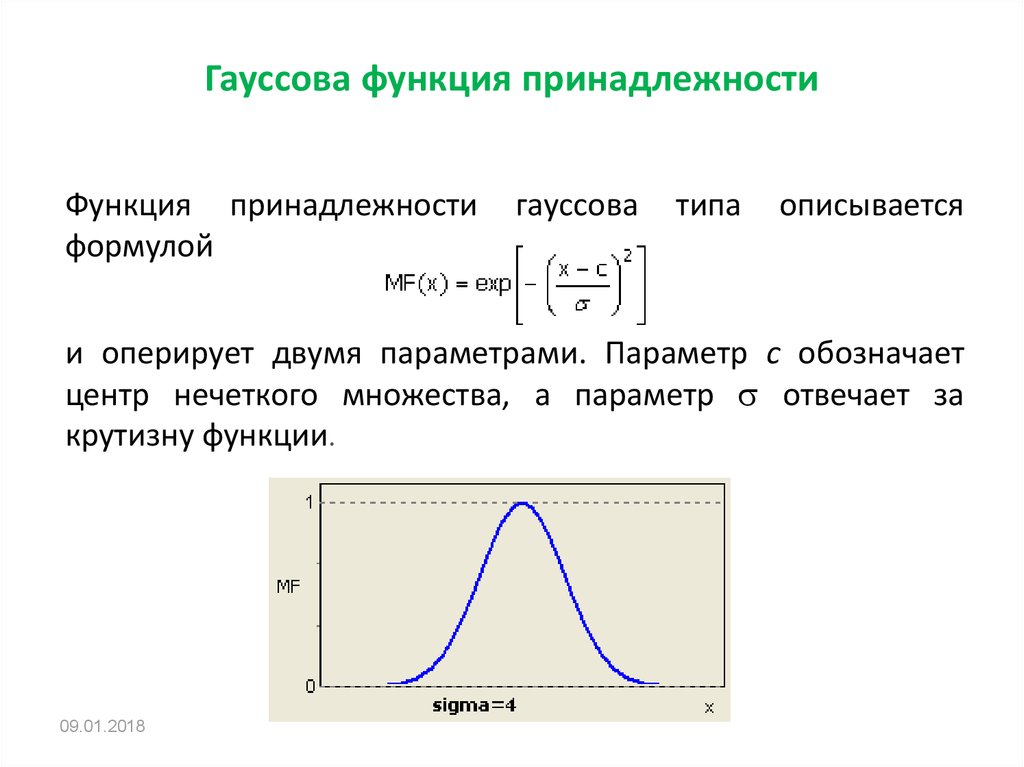
Для оптимизации вычислений и ускорения обработки данных рекомендуется использовать простые, но эффективные функции принадлежности, такие как треугольные или прямоугольные.

Функции принадлежности, основанные на логарифмических или экспоненциальных формулах, могут быть полезны при моделировании процессов с быстро изменяющимися степенями неопределенности.
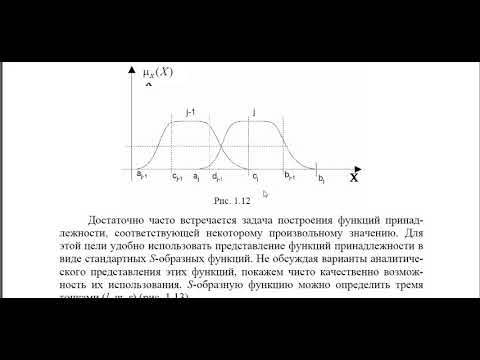
Ч 3 Функции принадлежности
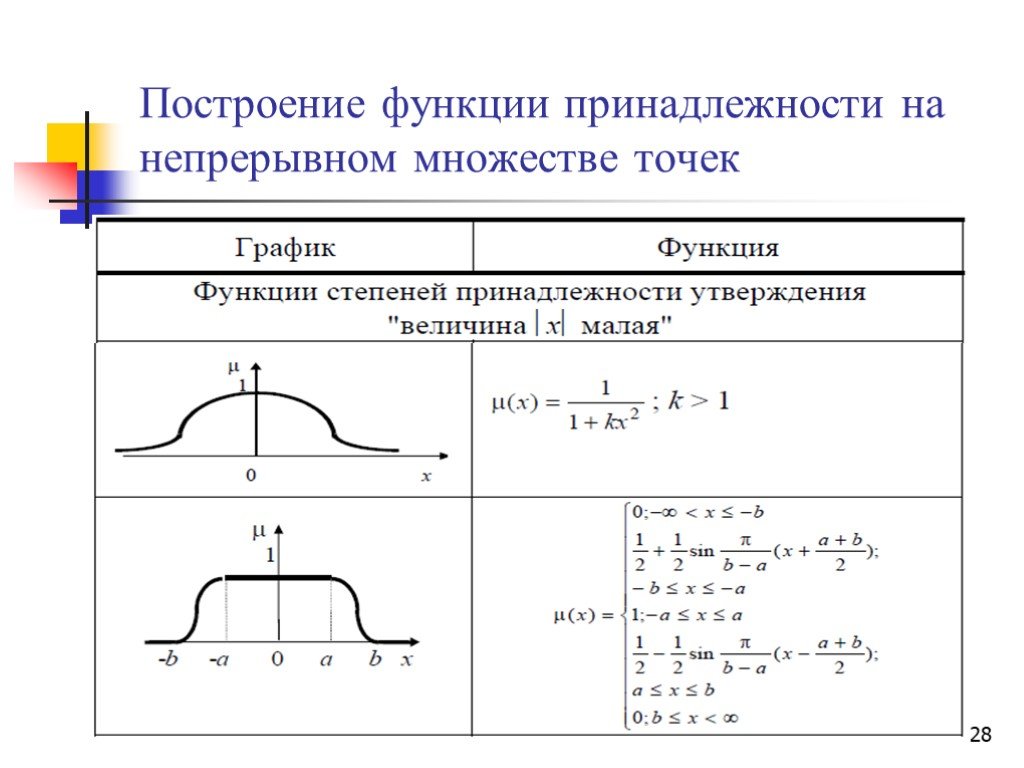

Что такое нечёткие переменные? Душкин объяснит
Функции принадлежности нечётких множеств в Mathcad
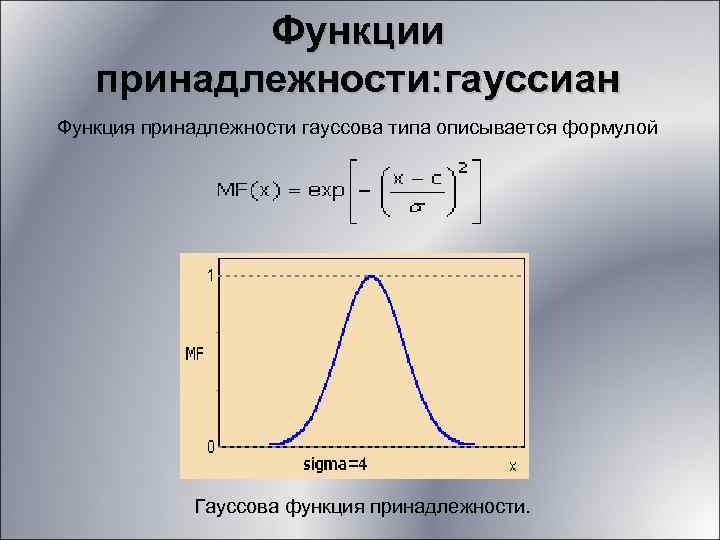

Обратите внимание на интерпретируемость функций принадлежности. В некоторых случаях, когда важна наглядность, проще использовать функции с очевидными геометрическими свойствами, такими как прямые или кривые линии.

R-анализ. Куча-3. Нечёткость

Постоянно анализируйте результаты применения функций принадлежности. В зависимости от контекста можно адаптировать или изменять выбор функции для улучшения точности и устойчивости модели.