Как теория Ляпунова помогает исследовать устойчивость решений в нелинейных системах
Теория Ляпунова является важным инструментом для анализа устойчивости динамических систем. Она позволяет предсказать поведение системы на основе её математической модели, определяя, как маленькие отклонения от равновесия могут повлиять на дальнейшее развитие процессов. В этой статье представлены примеры применения теории Ляпунова, которые помогут лучше понять, как она используется в реальных задачах.



При решении задач на устойчивость динамических систем всегда обращайте внимание на наличие векторных полей и их производных. Это поможет выявить точки равновесия.

Великий русский математик, академик Ляпунов, создатель теории устойчивости движения

Для точной оценки устойчивости системы, помимо теории Ляпунова, полезно использовать численные методы и симуляции.

Soothing music for nerves🌿 healing music for the heart and blood vessels, relaxation, music for soul
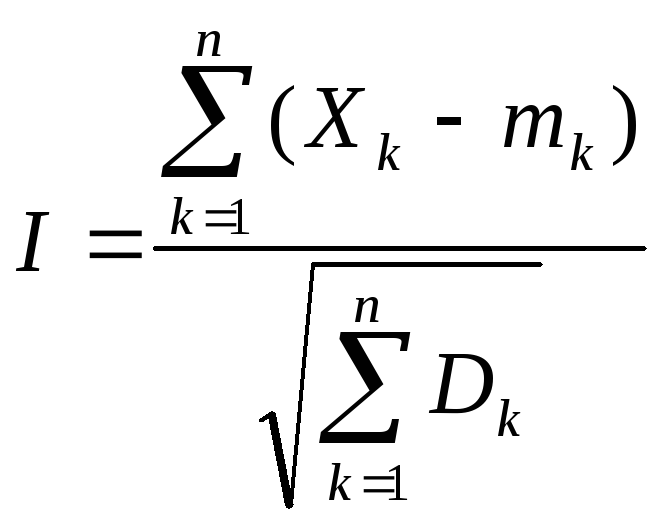
Обратите внимание на теорему Ляпунова, которая помогает установить локальную устойчивость системы при малых отклонениях.

РК6. Основы теории управления. Устойчивость САУ: основные понятия и теоремы Ляпунова
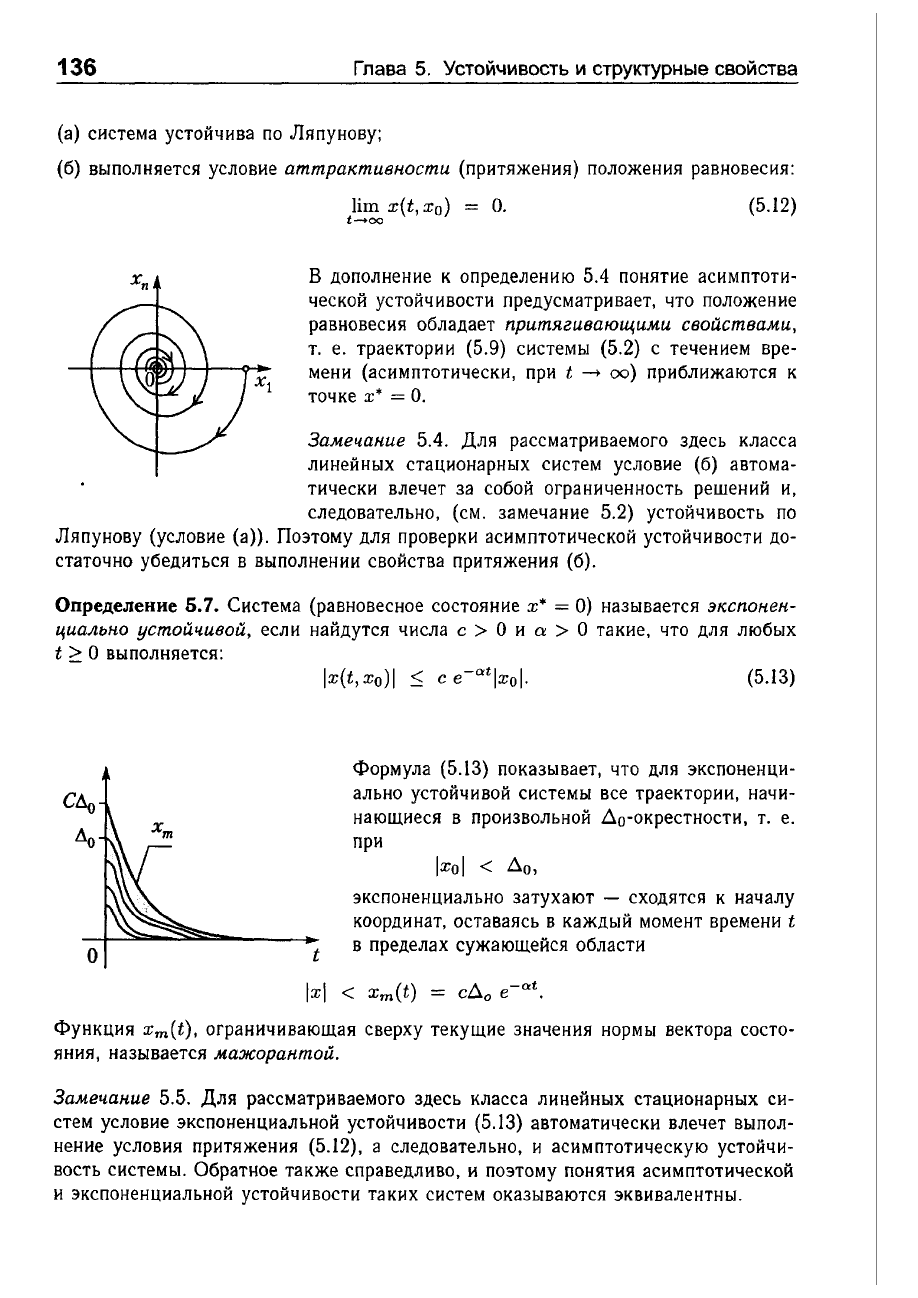
Не забывайте, что теория Ляпунова не всегда даёт полное решение, поэтому часто приходится использовать её в сочетании с другими методами анализа.

СЕМЬ ВЕЛИЧАЙШИХ ПРОБЛЕМ ТЫСЯЧЕЛЕТИЯ!

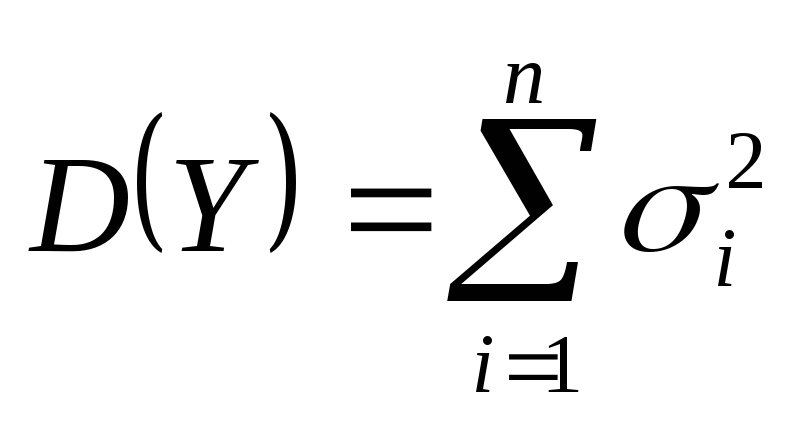
Если система нелинейная, старайтесь сначала линеаризовать её около равновесной точки, чтобы применить теорему Ляпунова более эффективно.
Основы второго метода Ляпунова


Важным моментом является выбор функции Ляпунова, которая должна быть положительно определённой и её производная — отрицательной.

Для сложных систем, в которых невозможно найти явную функцию Ляпунова, можно использовать численные методы для её приближенного построения.
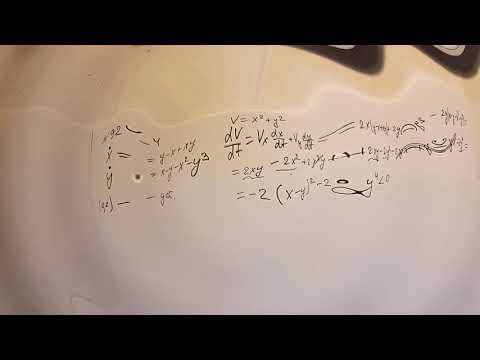
Функция Ляпунова 2 Примеры


Используйте примеры из теории Ляпунова в учебных задачах, чтобы развивать интуицию для более сложных приложений в инженерии и физике.

Функция Ляпунова 1 Теорема Ляпунова

Теория автоматического управления. Лекция 3. Второй метод Ляпунова
Не забывайте, что для глобальной устойчивости системы необходимо выполнить дополнительные проверки, выходящие за рамки стандартных методов.


Регулярно обновляйте знания о новых методах, основанных на теории Ляпунова, так как она активно развивается и находит новые применения в различных областях науки и техники.

Теория автоматического управления. Лекция 4. Поиск функций Ляпунова



Устойчивость по Ляпунову