Все важные теоремы о смежных и вертикальных углах для школьников 7 класса
На этой странице собраны основные теоремы о смежных и вертикальных углах, которые изучаются в 7 классе в рамках курса геометрии. Здесь вы найдете полезные советы, иллюстрации и подробные объяснения, которые помогут вам разобраться в этих важных концепциях и успешно подготовиться к урокам и экзаменам.
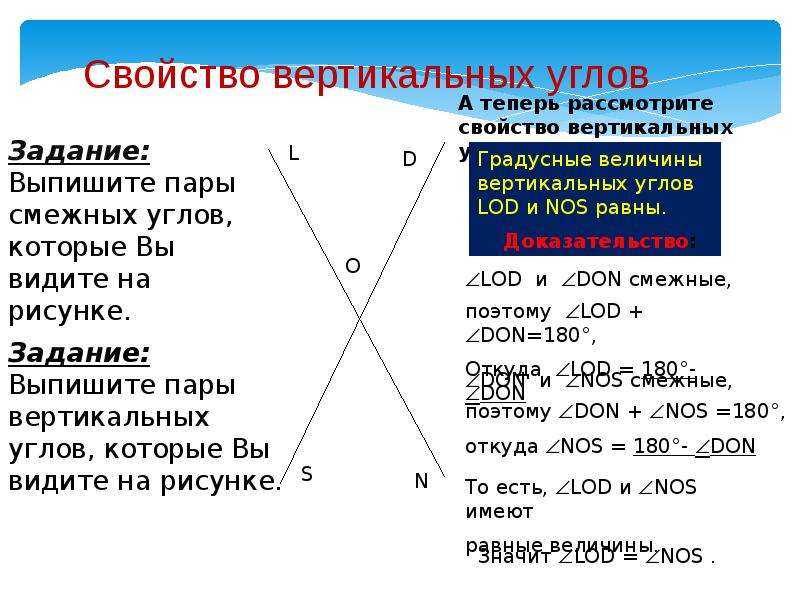

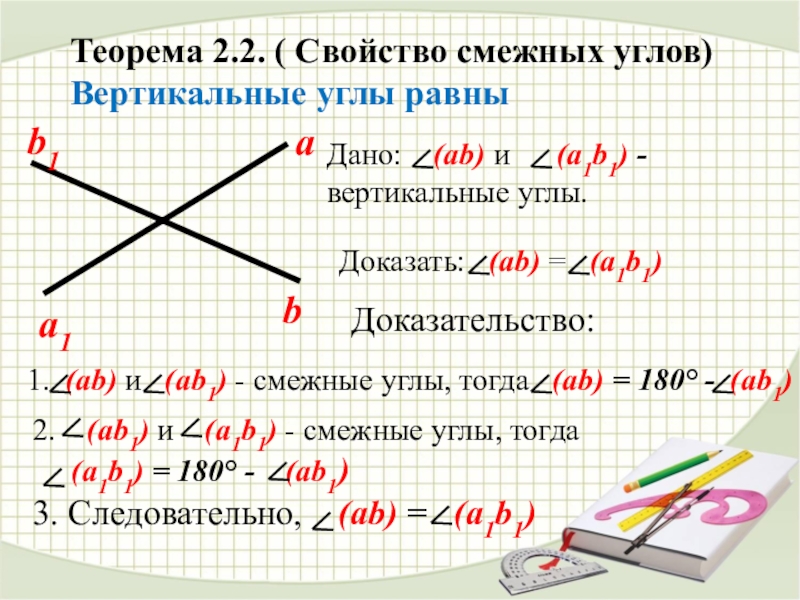
Для лучшего понимания смежных углов представьте себе два луча, исходящих из одной точки — угол между ними будет изменяться, а сумма смежных углов всегда равна 180°.

Основные понятия геометрии. Смежные и вертикальные углы. Часть 2. DİM 2023


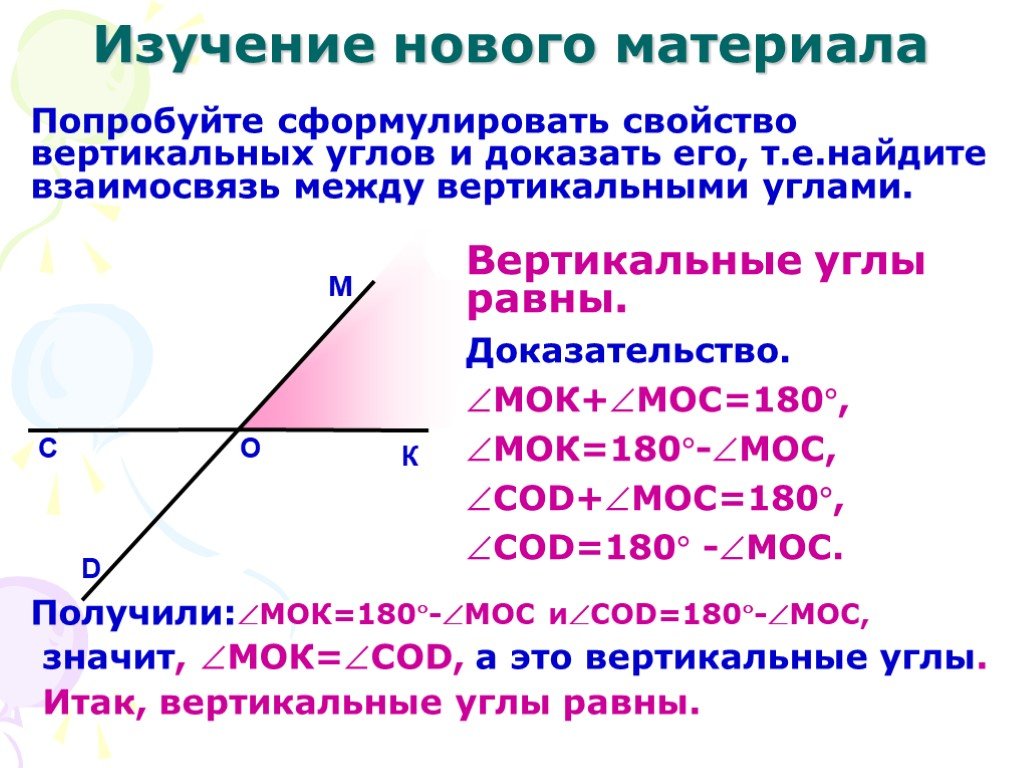
Не забывайте, что вертикальные углы всегда равны. Чтобы запомнить, попробуйте представить их как зеркальное отражение, где угол с одной стороны равен углу с другой.

Вертикальные углы. 7 класс.
Практикуйте решение задач с углами на практике — рисуйте фигуры, чтобы наглядно видеть, как работают теоремы о смежных и вертикальных углах.
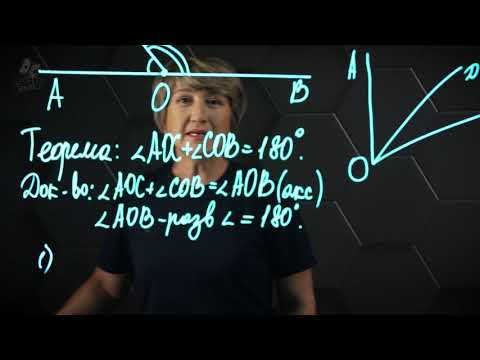
Смежные углы. 7 класс.
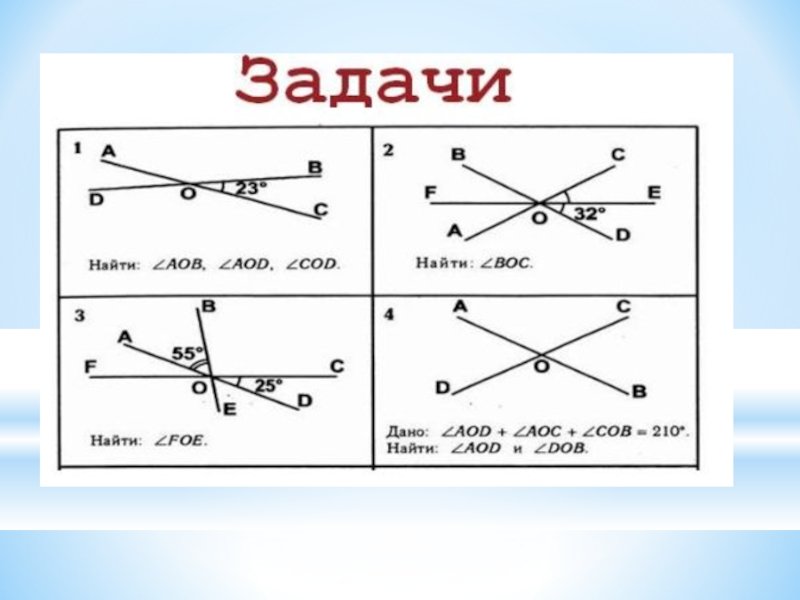

Обратите внимание на то, что смежные углы могут быть как острыми, так и тупыми. Углы, которые вместе составляют 180°, называются смежными.
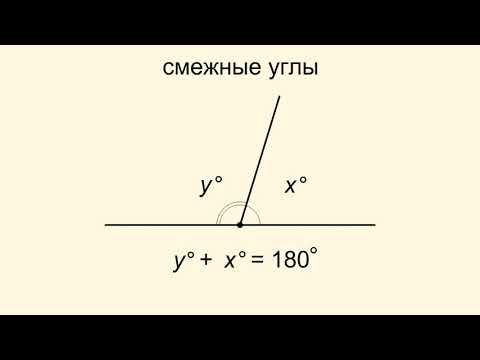
Смежные углы
Когда решаете задачи, всегда проверяйте, не образуют ли углы на рисунке пару смежных или вертикальных углов, это поможет упростить решение.

ГЕОМЕТРИЯ 7 КЛАСС: Смежные и Вертикальные Углы // Свойства углов

Используйте геометрические фигуры, чтобы легче понять теоремы: проведите лучи и линии, чтобы увидеть, как работают углы и их отношения.

Смежные и вертикальные углы. Аксиомы и теоремы


Запомните ключевое правило: если два угла смежные, их сумма всегда равна 180°. Это поможет вам правильно находить неизвестные углы.

Для теоремы о вертикальных углах важным моментом является то, что противоположные углы всегда равны, что может быть использовано для вычислений в задачах.

7 класс, 11 урок, Смежные и вертикальные углы

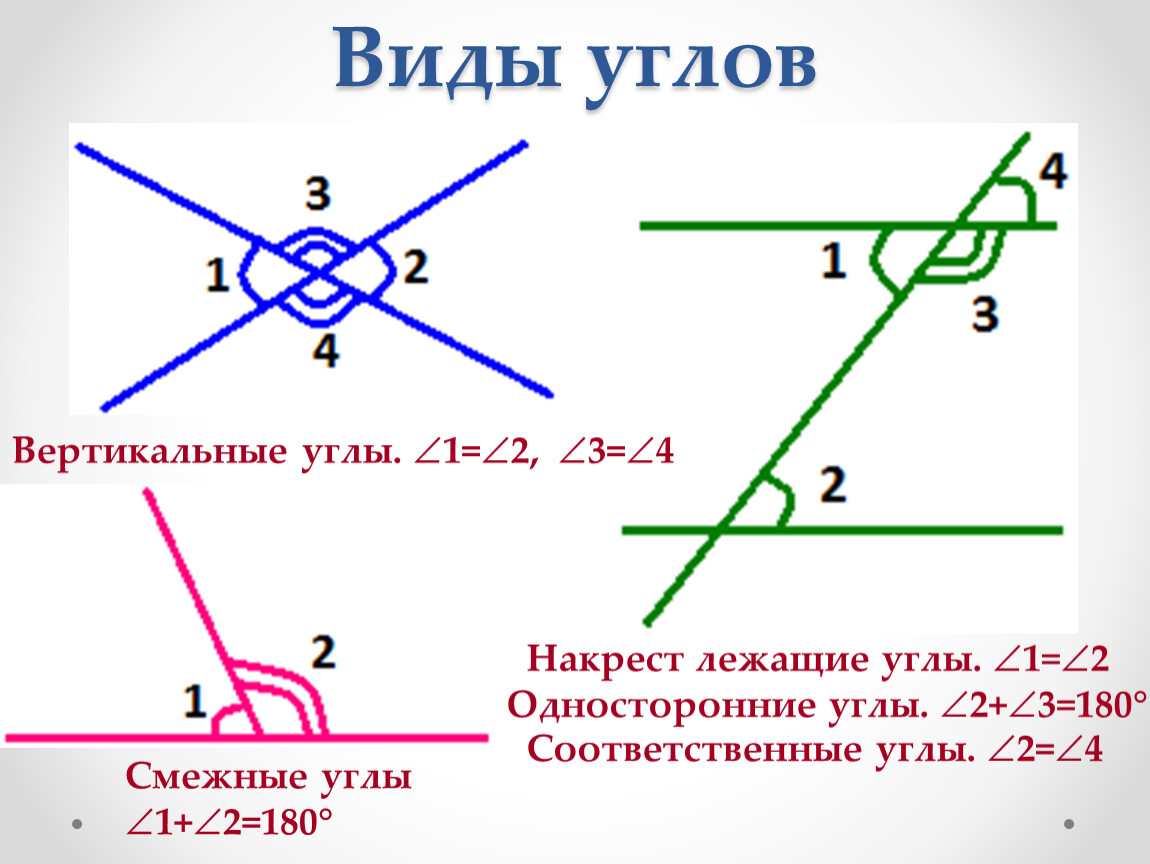
Не забывайте, что смежные углы могут образовываться не только прямыми линиями, но и другими фигурами, например, углами пересекающихся прямых.
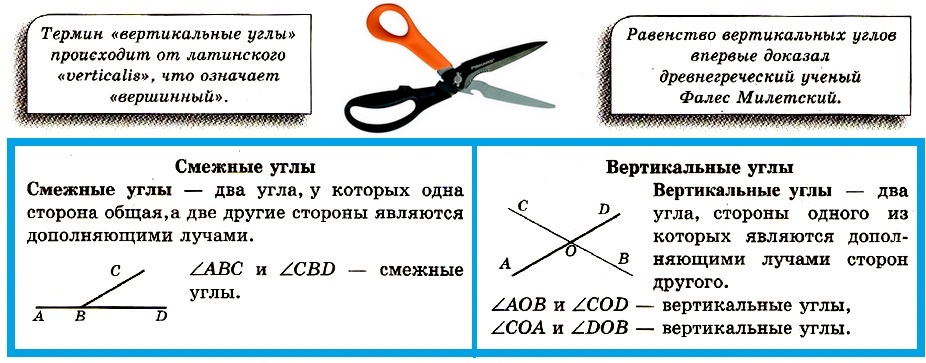
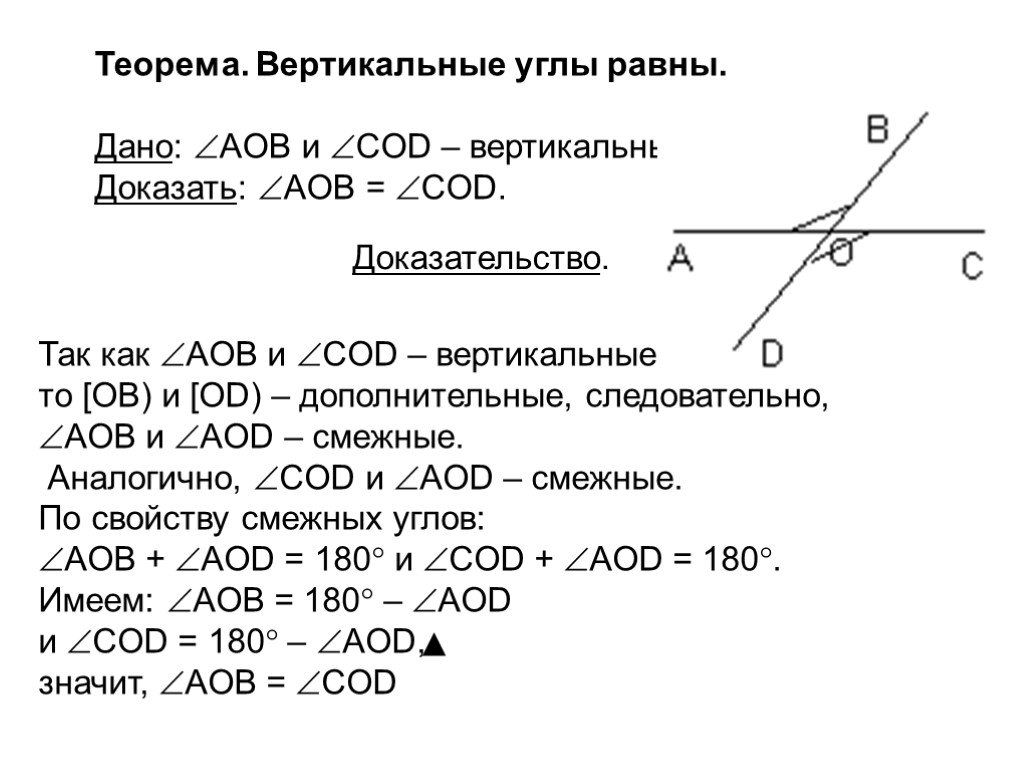
Чтобы быстрее решать задачи, запоминайте, что угол между двумя пересекающимися прямыми всегда может быть представлен через вертикальные углы, которые равны между собой.

SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы - Математика TutorOnline

Смежные и вертикальные углы. Практическая часть - решение задачи. 7 класс.