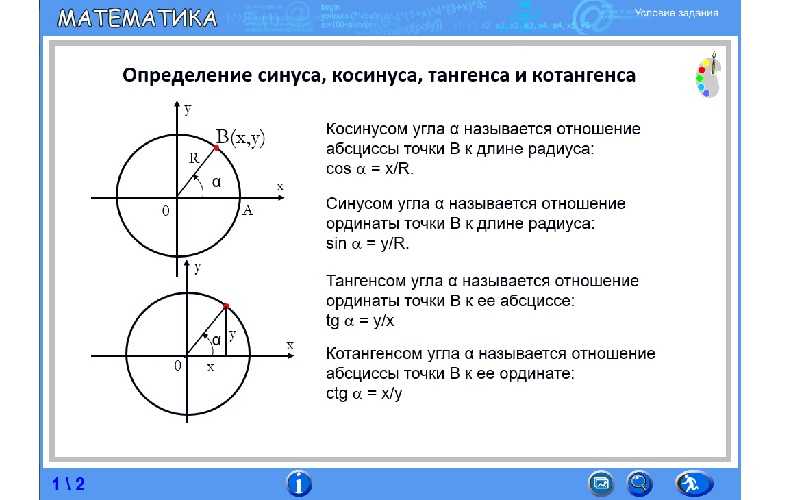
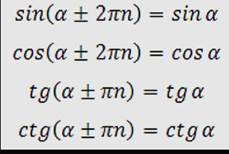Основные свойства тригонометрических функций синуса, косинуса, тангенса и котангенса
На этой странице собраны основные свойства тригонометрических функций синуса, косинуса, тангенса и котангенса. Мы предлагаем полезные советы и методики, которые помогут вам глубже понять и применять эти функции при решении математических задач. Эти знания полезны как для школьников, так и для студентов, а также для тех, кто готовится к экзаменам.
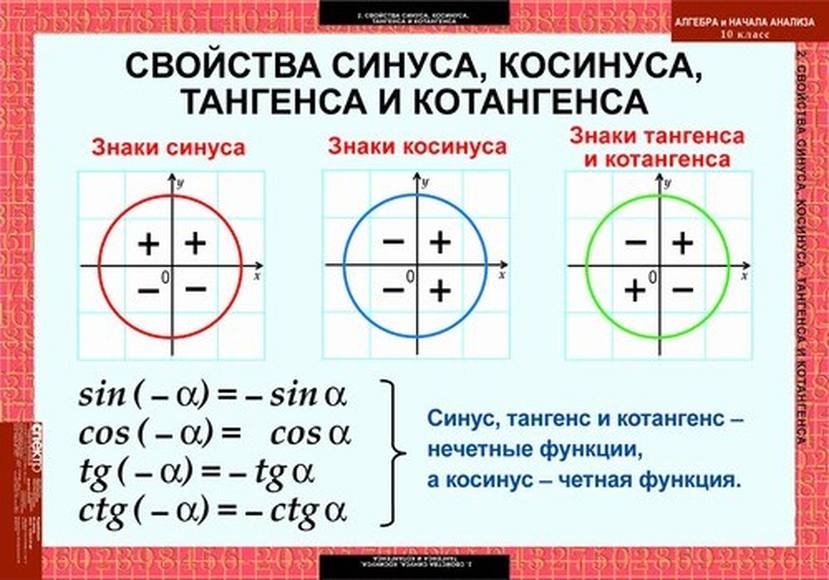

Для запоминания значений тригонометрических функций на определенных углах используйте ассоциации с координатами на единичной окружности.

10 класс. Синус и косинус. Тангенс и котангенс. Часть 1. Свойства синуса и косинуса
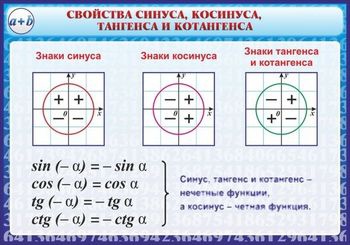
При решении задач на нахождение значений тригонометрических функций на разных углах важно учитывать периодичность этих функций.

Синус, косинус, тангенс, котангенс за 5 МИНУТ
Не забывайте, что синус и косинус являются функциями с одинаковым периодом, а тангенс и котангенс имеют период 180° или π.

ТРИГОНОМЕТРИЯ с нуля — Синус, косинус, тангенс и котангенс острого угла
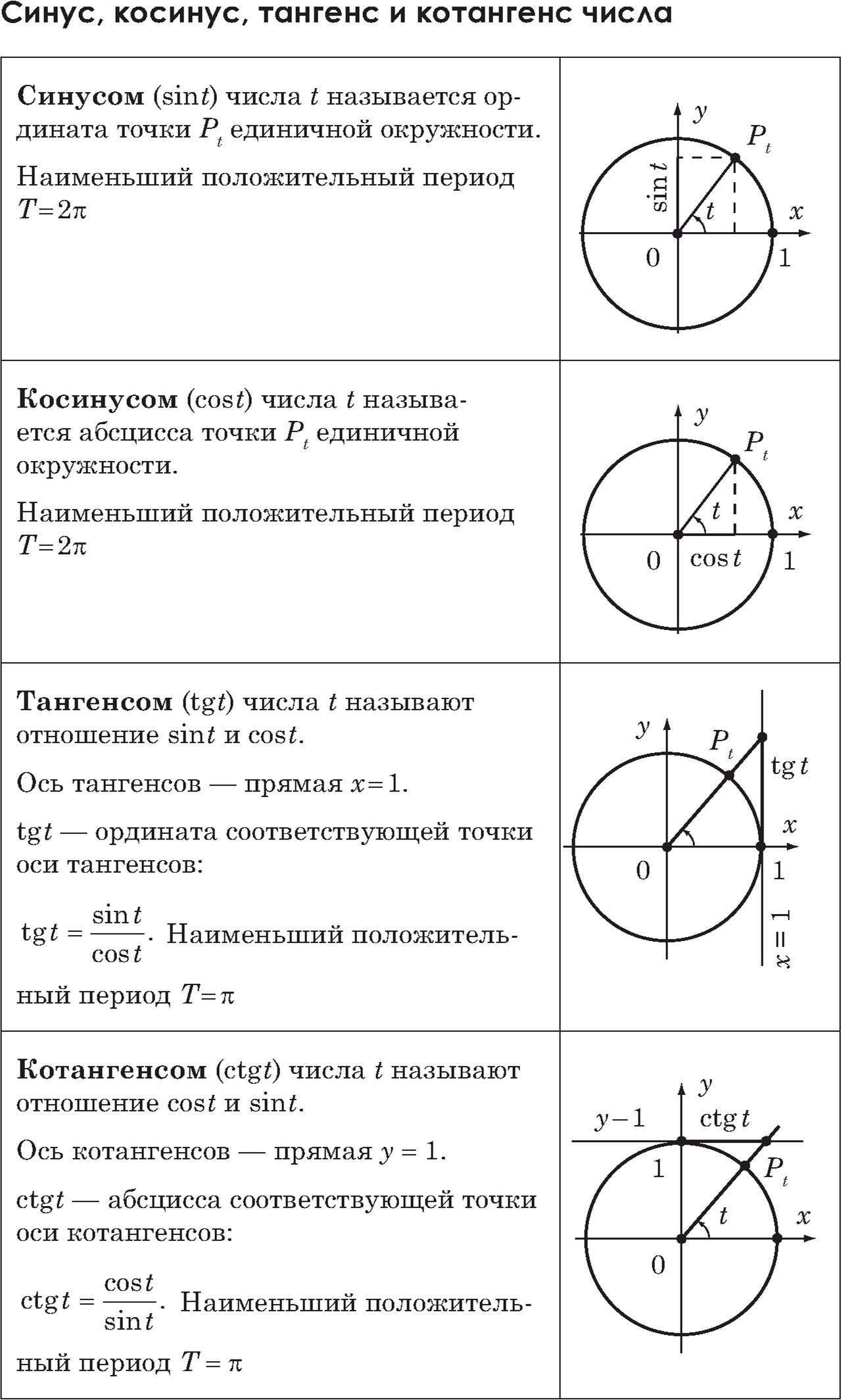
Для упрощения выражений с тригонометрическими функциями часто используется формула приведения.

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Синус, Косинус, Тангенс, Котангенс // Подготовка к ЕГЭ по Математике
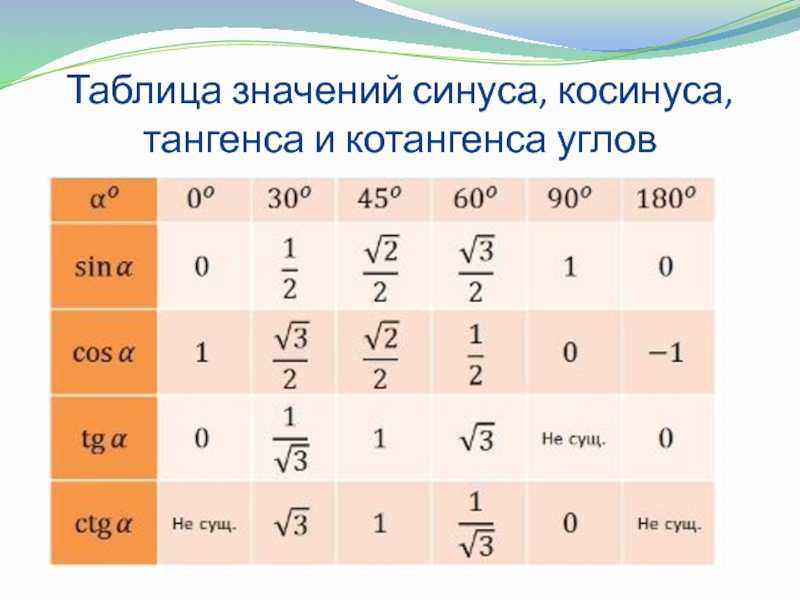
Понимание геометрической интерпретации тригонометрических функций помогает лучше осваивать их свойства.

10 класс, 16 урок, Функции y=sinx, y=cosx, их свойства и графики

Для эффективного решения уравнений с тригонометрическими функциями используйте идентичности и преобразования тригонометрических функций.
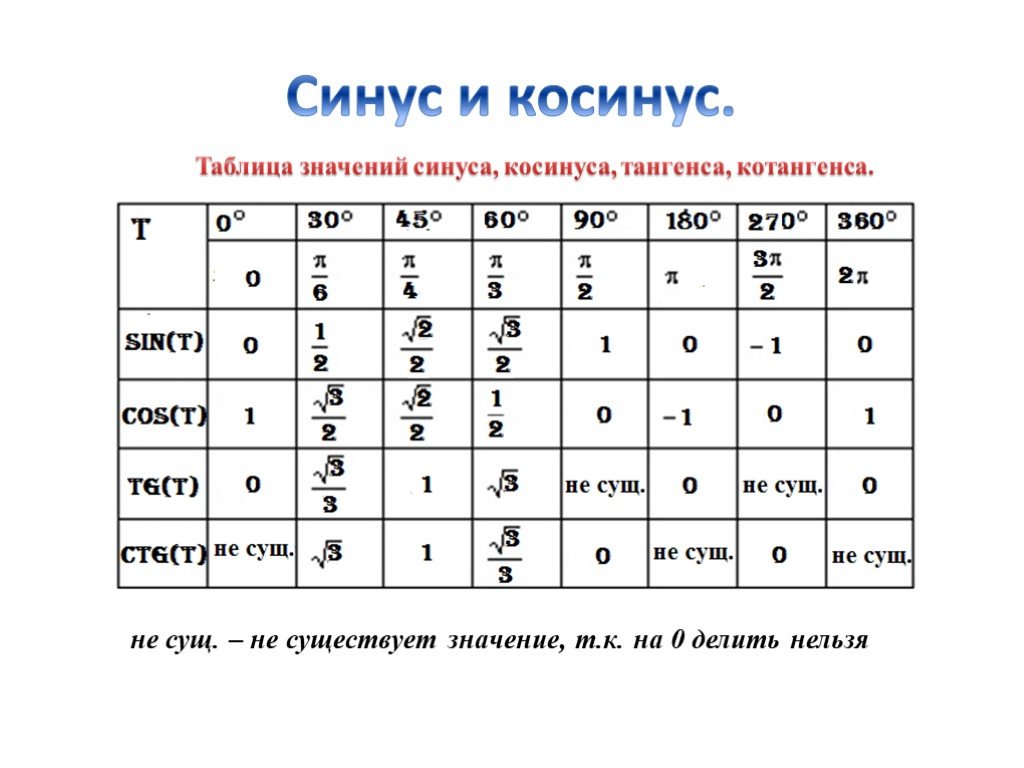
Запомните основные тождества для синуса, косинуса, тангенса и котангенса, такие как Pythagorean identity.

Зачем нужны тангенсы?


Регулярно решайте практические задачи для закрепления теории и выявления закономерностей в тригонометрических функциях.
Тангенс и котангенс могут быть представлены как отношение синуса и косинуса, что поможет упростить вычисления.


Если вам сложно запомнить все формулы, попробуйте использовать графики, которые наглядно покажут поведение этих функций на различных интервалах.