Разбор свойств параболы в квадратичных функциях с примерами
На этой странице вы найдете подборку фотографий и полезные советы, которые помогут разобраться в свойствах параболы, изучить поведение графика квадратичной функции и понять основные особенности ее построения.

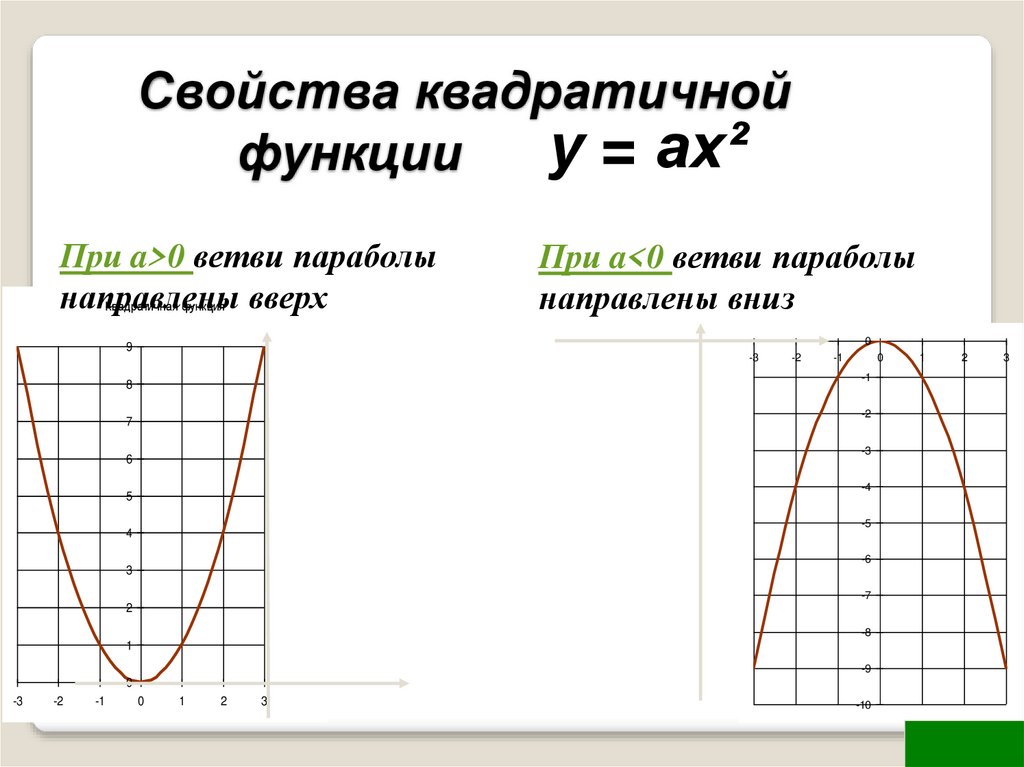
Определите направление ветвей параболы: если коэффициент перед x² положительный, ветви направлены вверх, если отрицательный — вниз.

А вы знали эти свойства параболы?


Вершина параболы — это ключевая точка, которую можно найти по формуле: x = -b/(2a).
Квадратичная функция и ее график. 8 класс.

График квадратичной функции симметричен относительно вертикальной прямой, проходящей через вершину.

ОБЪЯСНЕНИЕ ГРАФИКА ПАРАБОЛЫ 😉 ЧАСТЬ I #shorts #егэ #огэ #математика #проценты
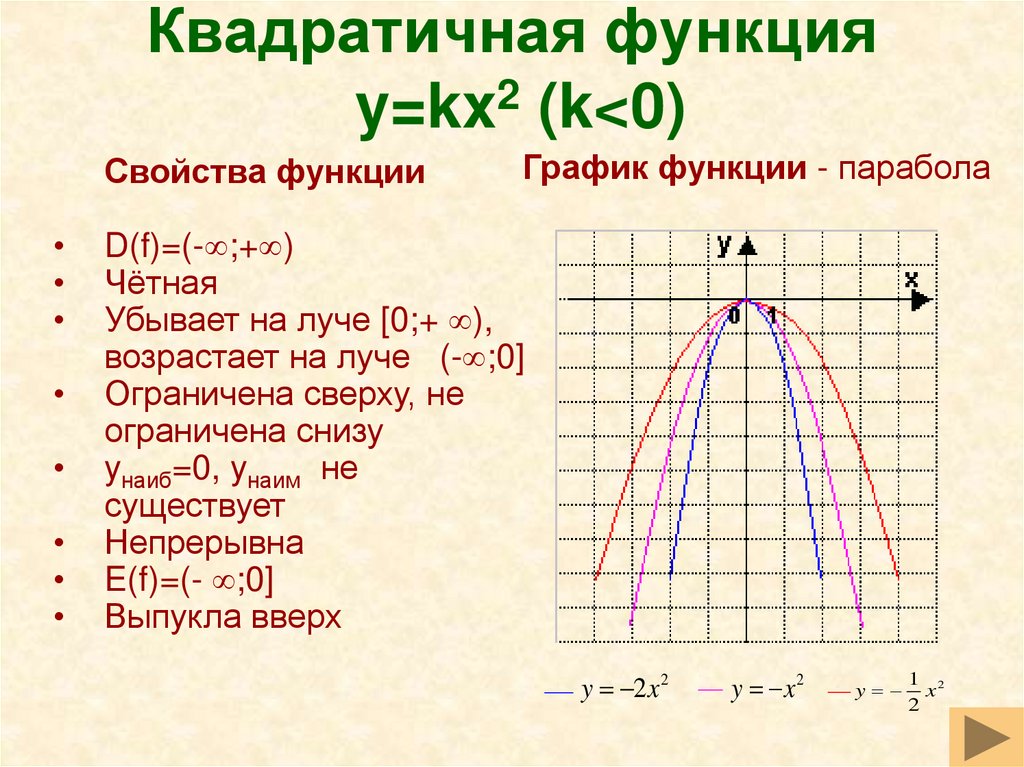
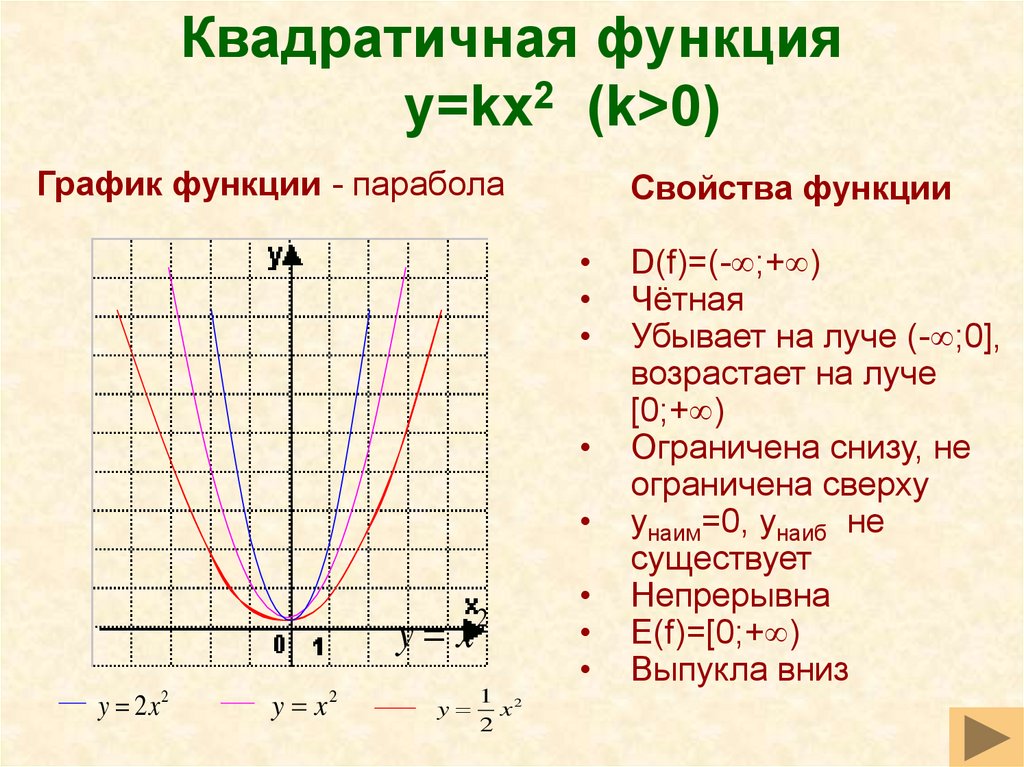
Для точного построения параболы найдите координаты вершины и нескольких точек по обе стороны от нее.

ГРАФИК КВАДРАТИЧНОЙ ФУНКЦИИ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэ
При анализе свойств параболы обратите внимание на значения коэффициентов a, b и c в уравнении y = ax² + bx + c.

ТЕПЕРЬ ТЫ ЛЕГКО ПОЙМЕШЬ свойства квадратичной функции — Парабола
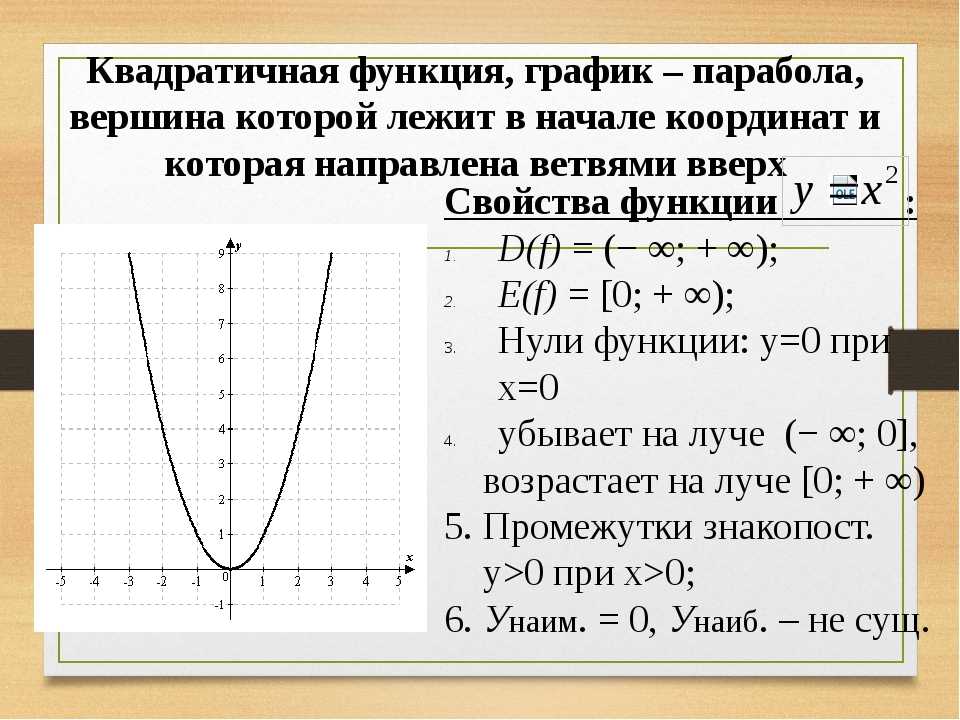
Парабола имеет одну точку минимума или максимума, которая совпадает с вершиной графика.
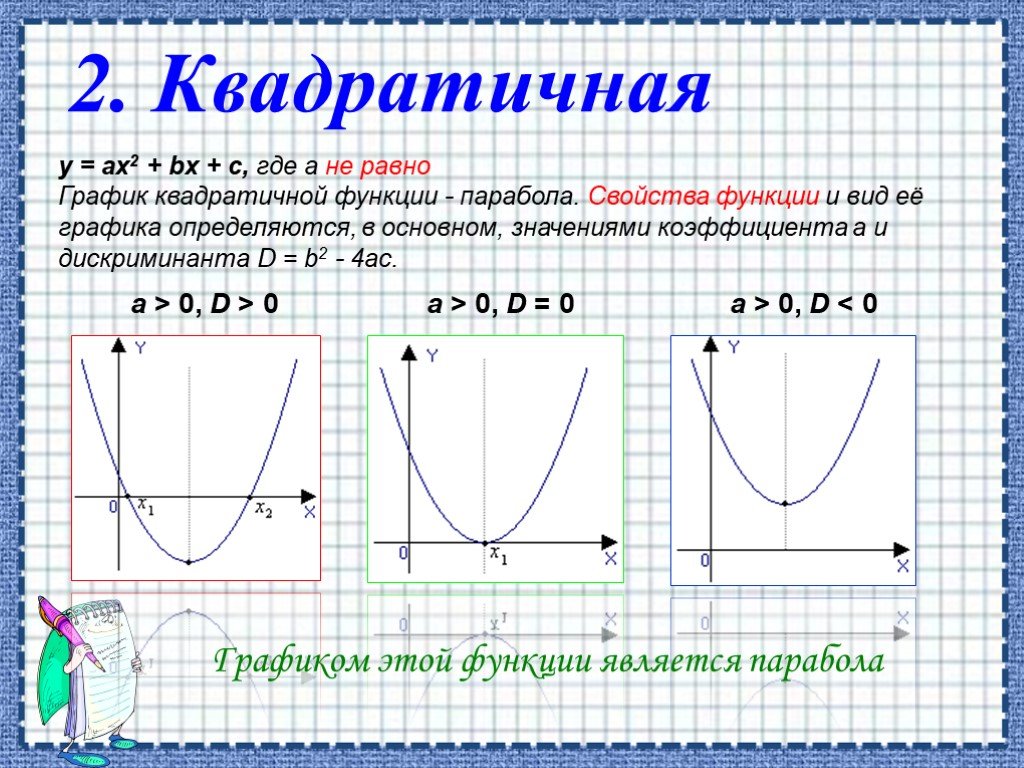
Область определения квадратичной функции — вся числовая прямая.

ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график Парабола
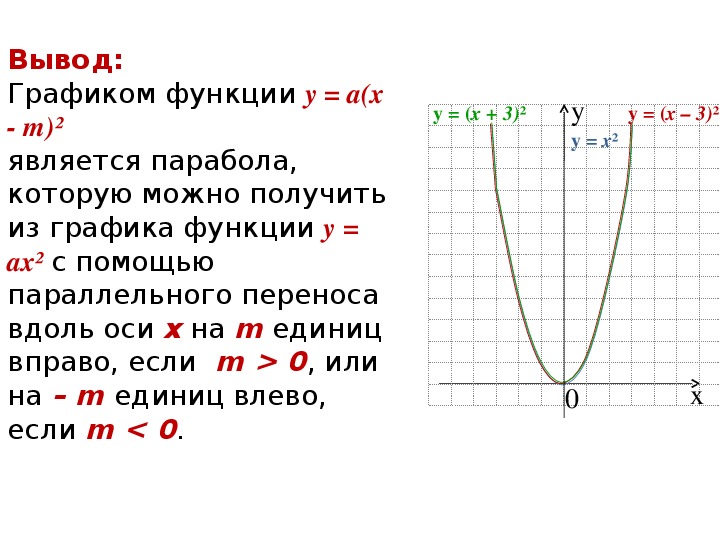
Область значений функции зависит от направления ветвей: при ветвях вверх y ≥ y₀, при ветвях вниз y ≤ y₀ (где y₀ — координата вершины).

УЧИМСЯ ПОНИМАТЬ ПАРАБОЛУ. Свойства и лайфхаки квадратичной функции


Для проверки построенного графика используйте подстановку нескольких значений x в исходное уравнение.

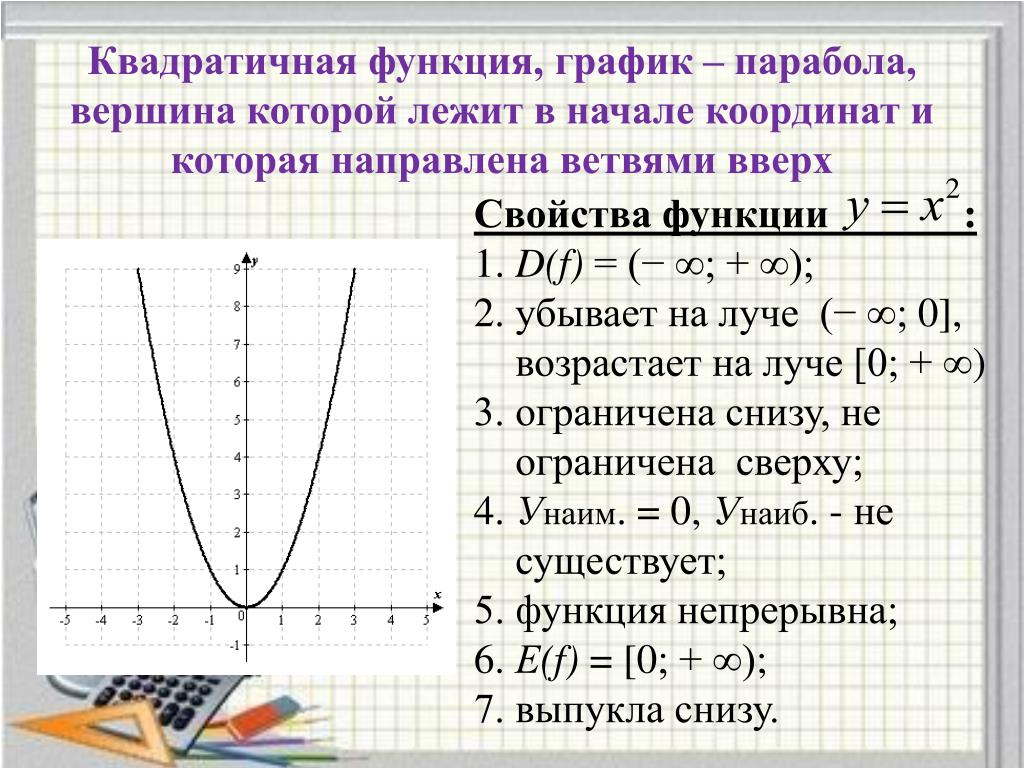
При решении задач с параболой всегда обращайте внимание на точность вычислений коэффициентов и координат ключевых точек.
