Особенности и характеристики диагоналей квадрата: что важно знать
Диагонали квадрата играют ключевую роль в его геометрических свойствах. Они не только равны по длине, но и пересекаются под прямым углом, делая квадрат уникальной фигурой. Узнайте больше о этих важных характеристиках и их применении в задачах.
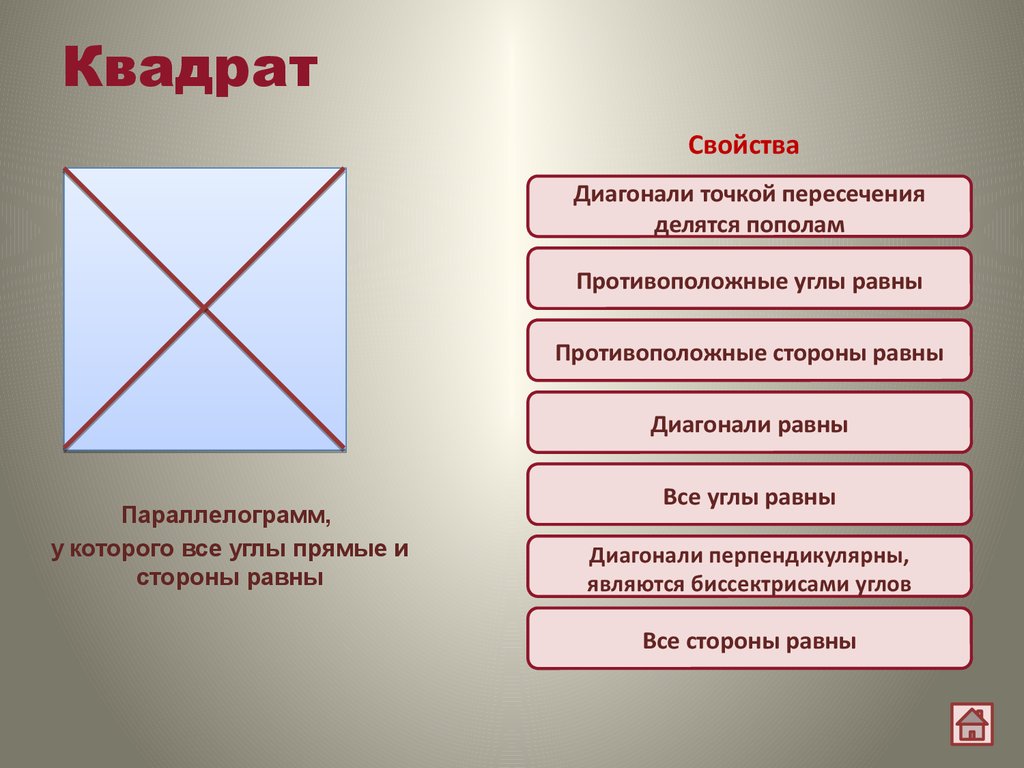
При вычислении длины диагонали квадрата можно воспользоваться теоремой Пифагора, поскольку диагональ является гипотенузой прямоугольного треугольника, образованного двумя сторонами квадрата.

Прямоугольник . Квадрат. Периметр. Свойства диагоналей. Математика. 5 класс.
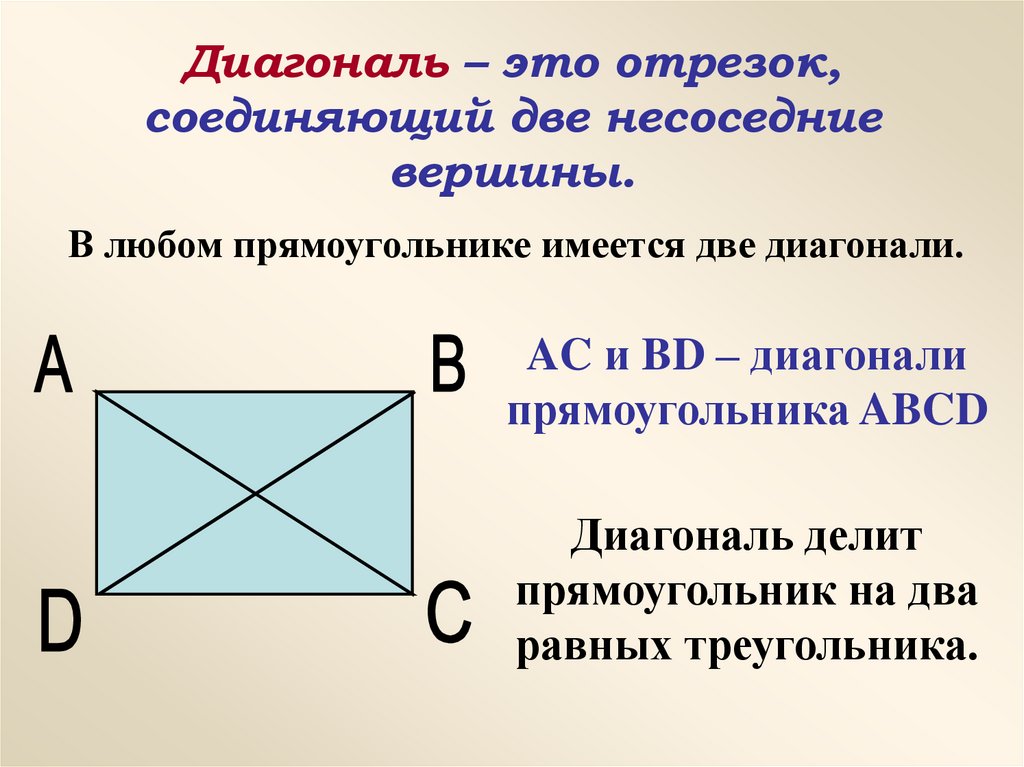
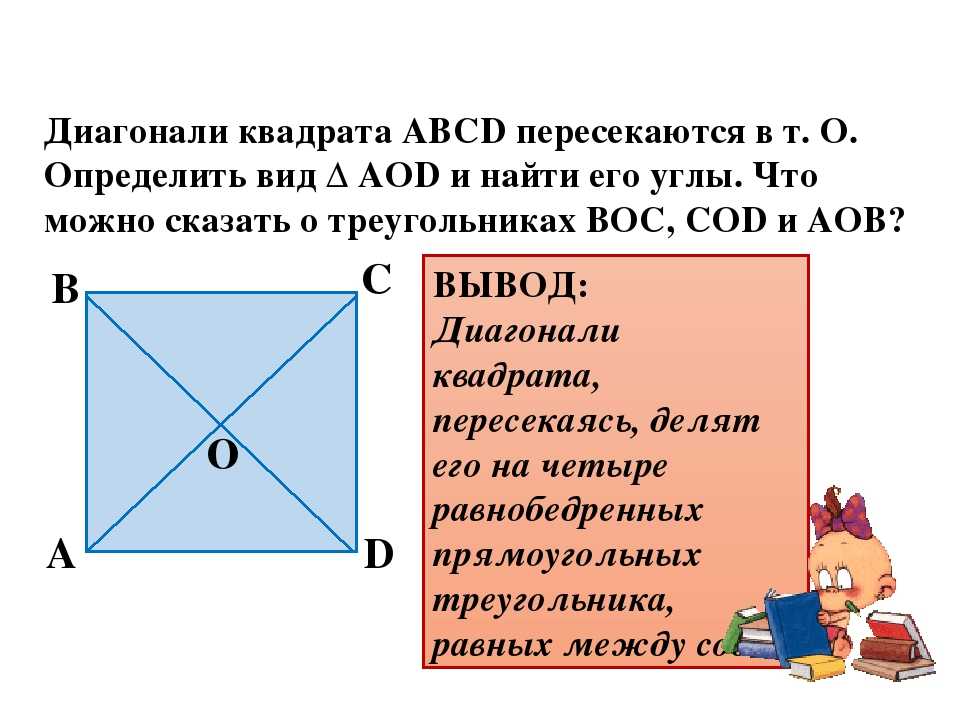
Диагонали квадрата пересекаются под прямым углом, что делает угол между ними равным 90 градусам.

КАК ВЫСТАВИТЬ ДИАГОНАЛЬ ФУНДАМЕНТА / КАК РАЗМЕТИТЬ ФУНДАМЕНТ своими руками
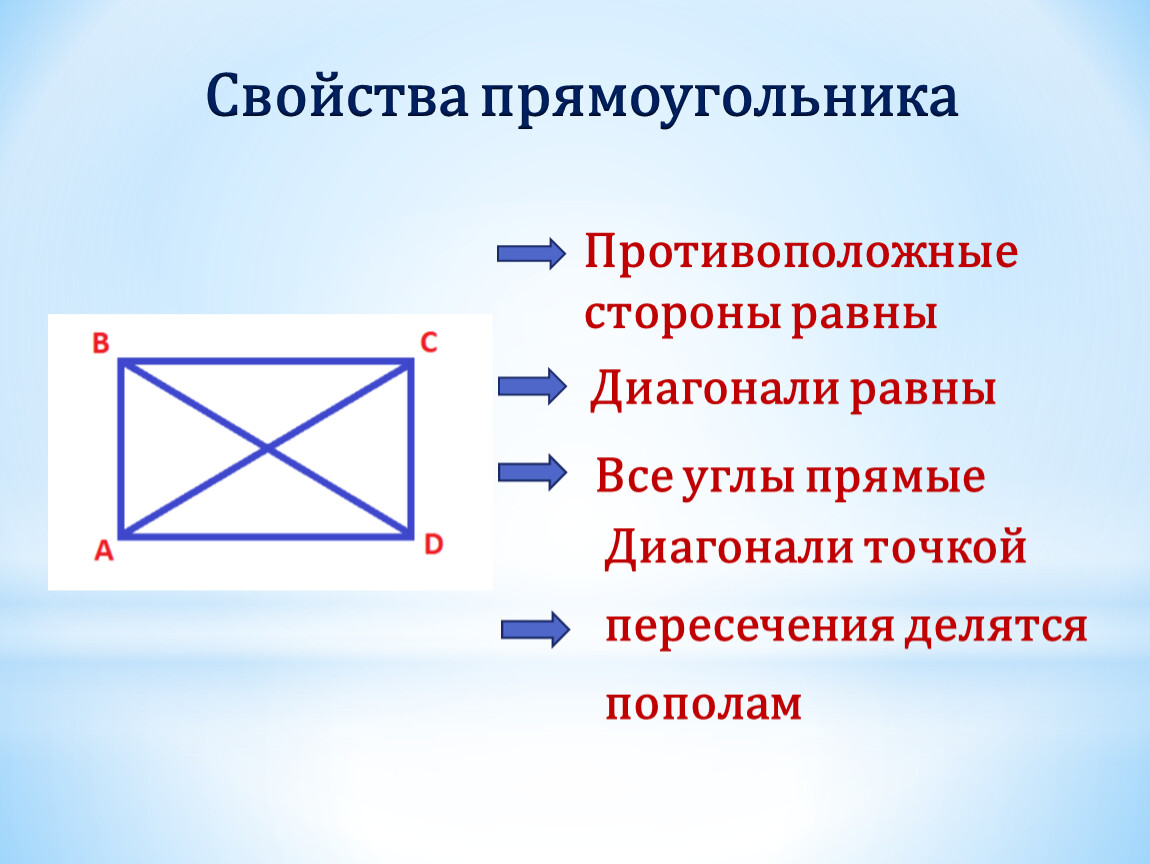
Каждая диагональ квадрата делит его на два равных прямоугольных треугольника, что позволяет использовать симметричные свойства фигуры для решения задач.

Проверяю контрольную работу по математике 4 класс

Диагонали квадрата одинаковы по длине, что подтверждает его симметрию и равенство сторон.

Свойства диагоналей
Если известно значение стороны квадрата, длину диагонали можно найти по формуле: d = √2 * a, где a — длина стороны квадрата.
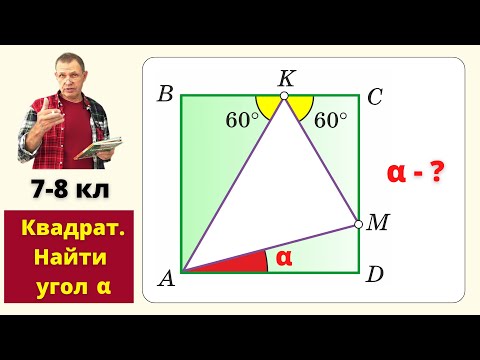
ЗАДАЧА ВЗОРВАЛА ИНТЕРНЕТ! НИКТО НЕ РЕШИЛ!

Для доказательства перпендикулярности диагоналей квадрата можно использовать свойство, что сумма углов в любом треугольнике равна 180 градусам.
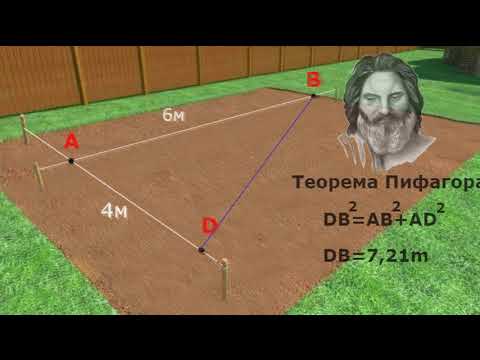
Разметка под фундамент
Диагонали квадрата равны по длине, что позволяет использовать их для нахождения площади фигуры через формулу: S = (d²)/2, где d — длина диагонали.

Теорема о четырех красках – простая задача с непростым решением // Vital Math
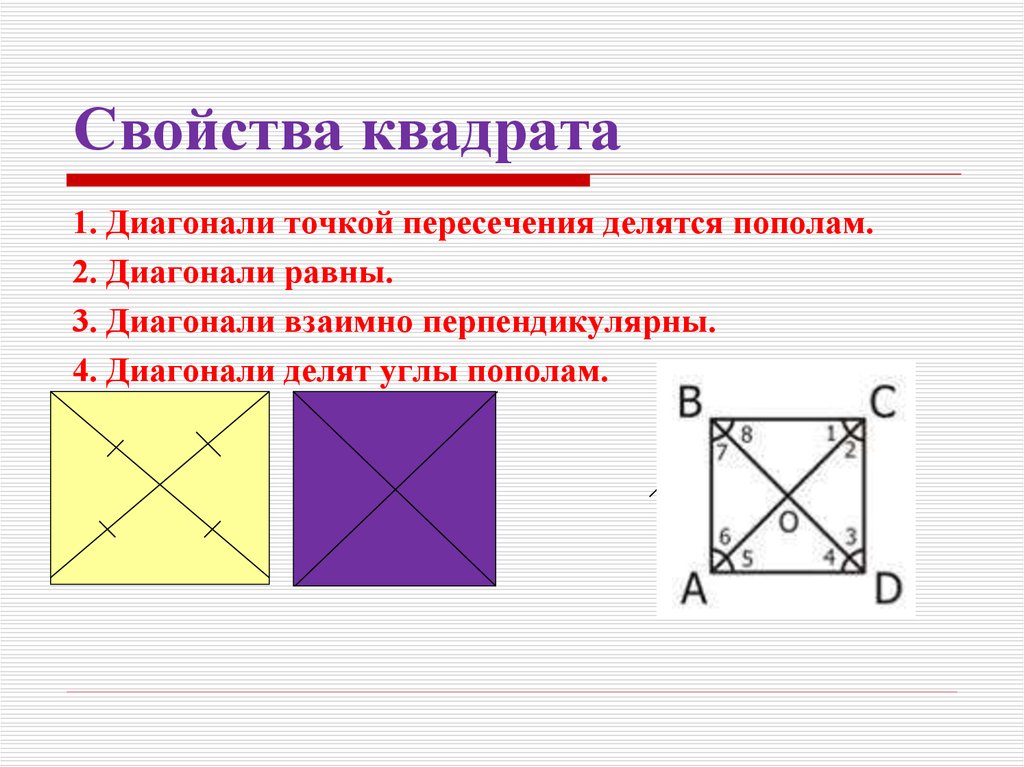
Зная длину диагонали квадрата, можно легко вычислить его периметр, так как он равен 4 * a, где a — длина стороны квадрата.

4-класс - Математика - Свойства диагоналей прямоугольника и квадрата

Диагонали квадрата делят его на 4 равных прямоугольных треугольника, что удобно для использования в геометрических доказательствах.


Применяя свойства диагоналей квадрата, можно решить задачи на нахождение углов, периметра и площади, используя только геометрические методы.