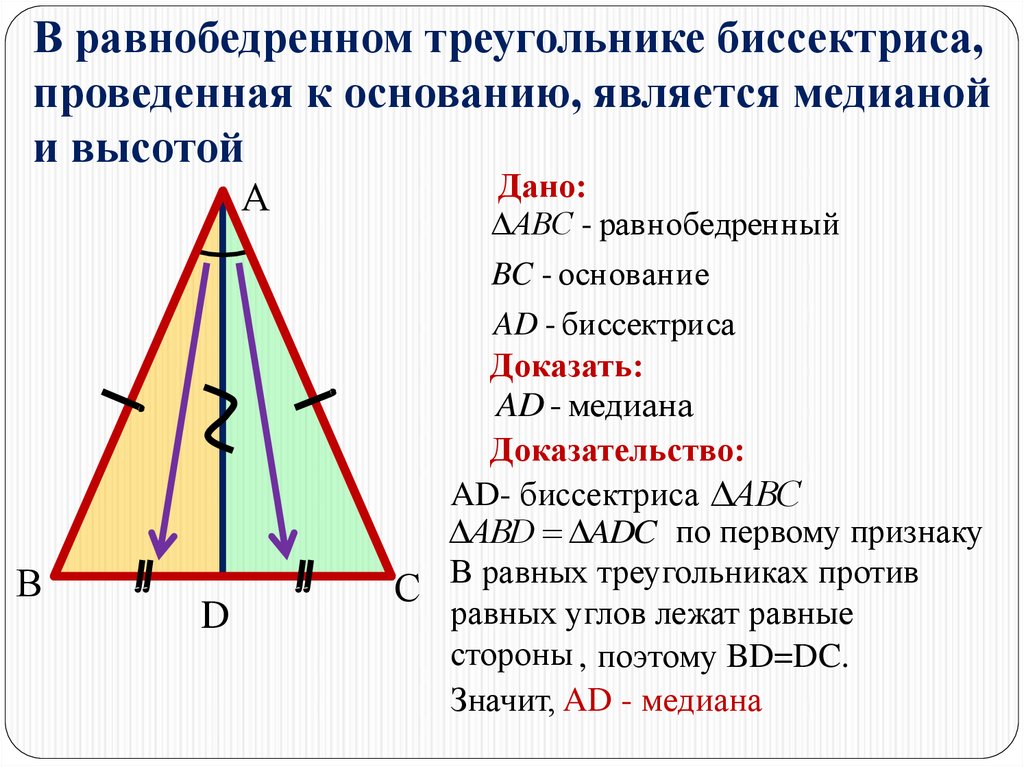
Секреты равнобедренного треугольника: формулы и советы
На этой странице вы найдете полезные советы и ключевые соотношения, которые помогут лучше понять свойства равнобедренного треугольника и эффективно использовать их в расчетах.
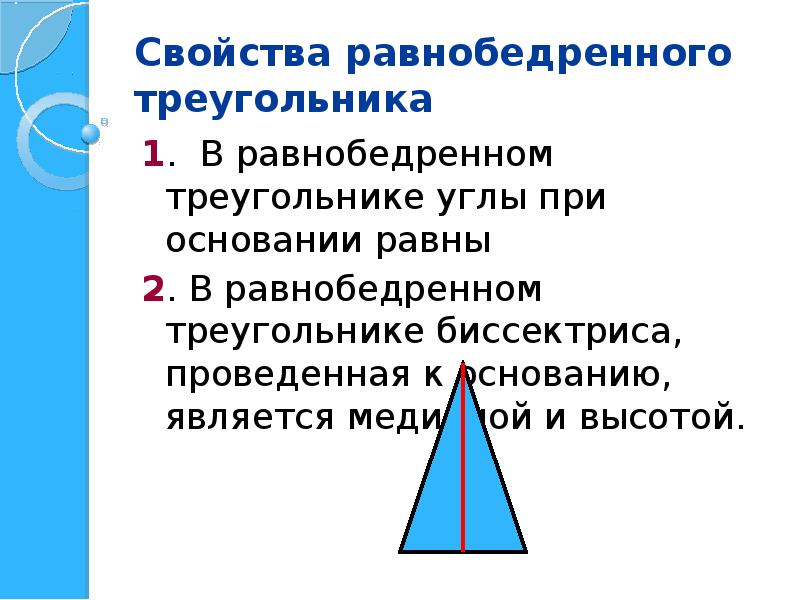
Помните, что углы при основании равнобедренного треугольника всегда равны.

Равнобедренный треугольник. 7 класс.
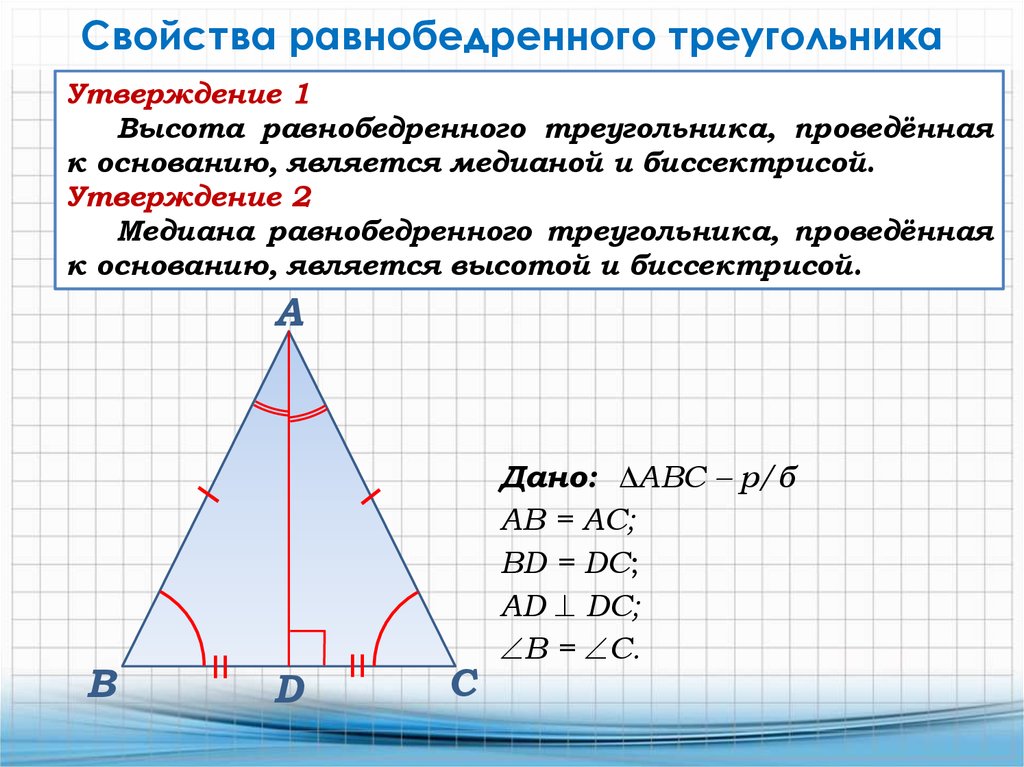

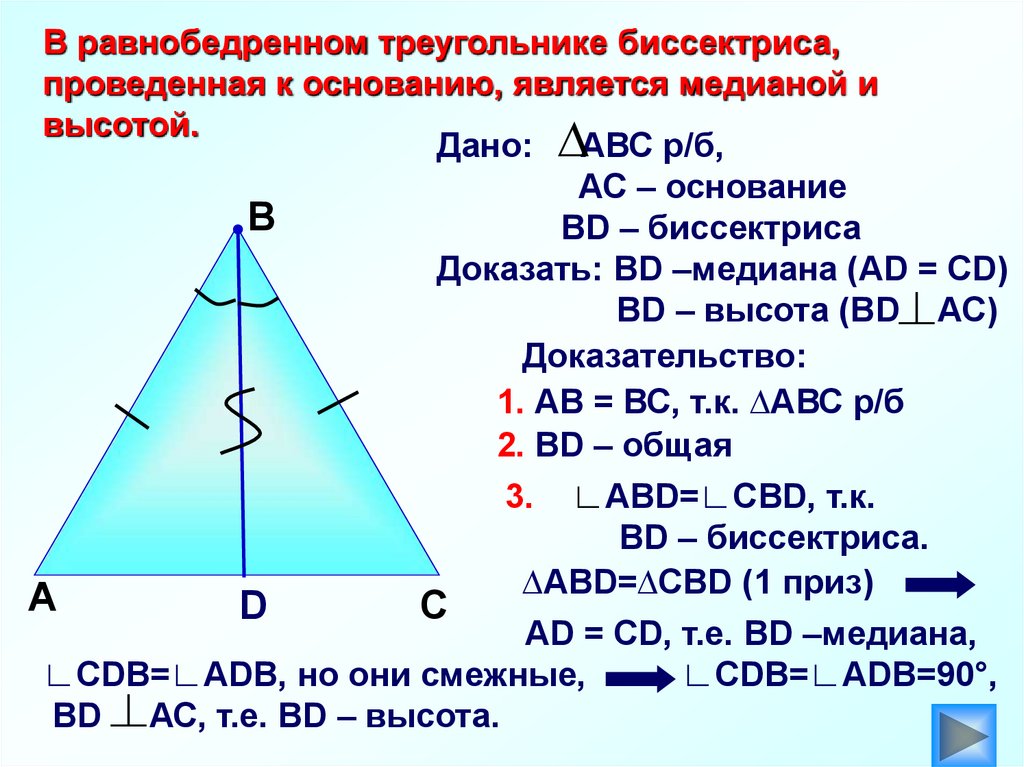
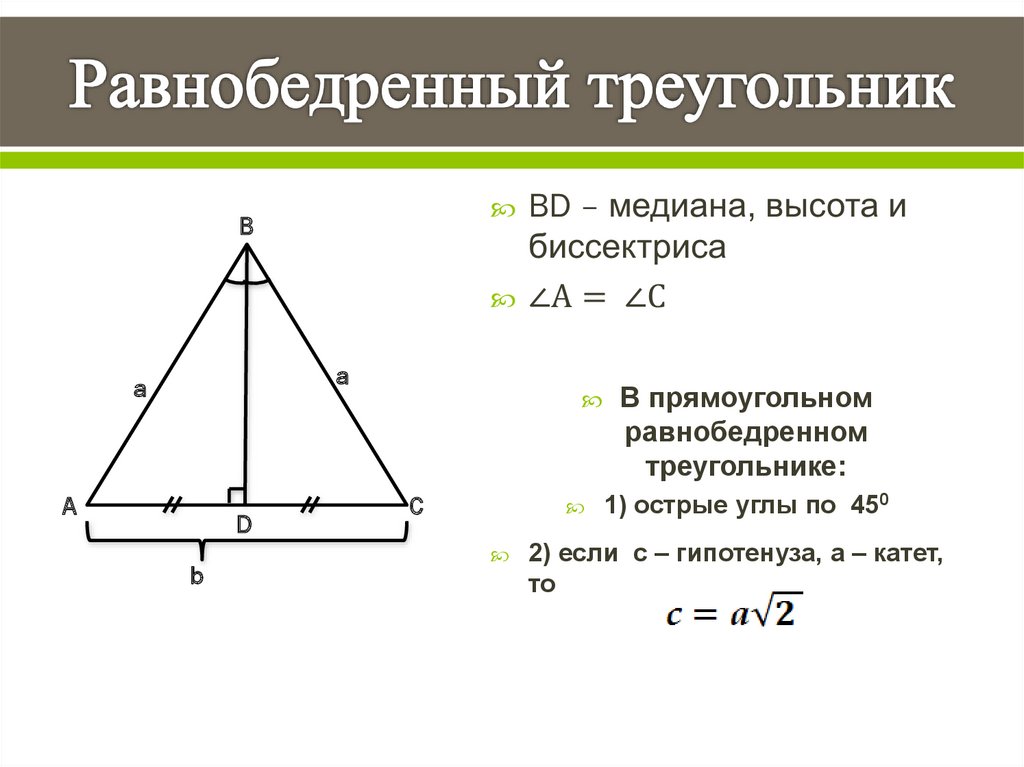
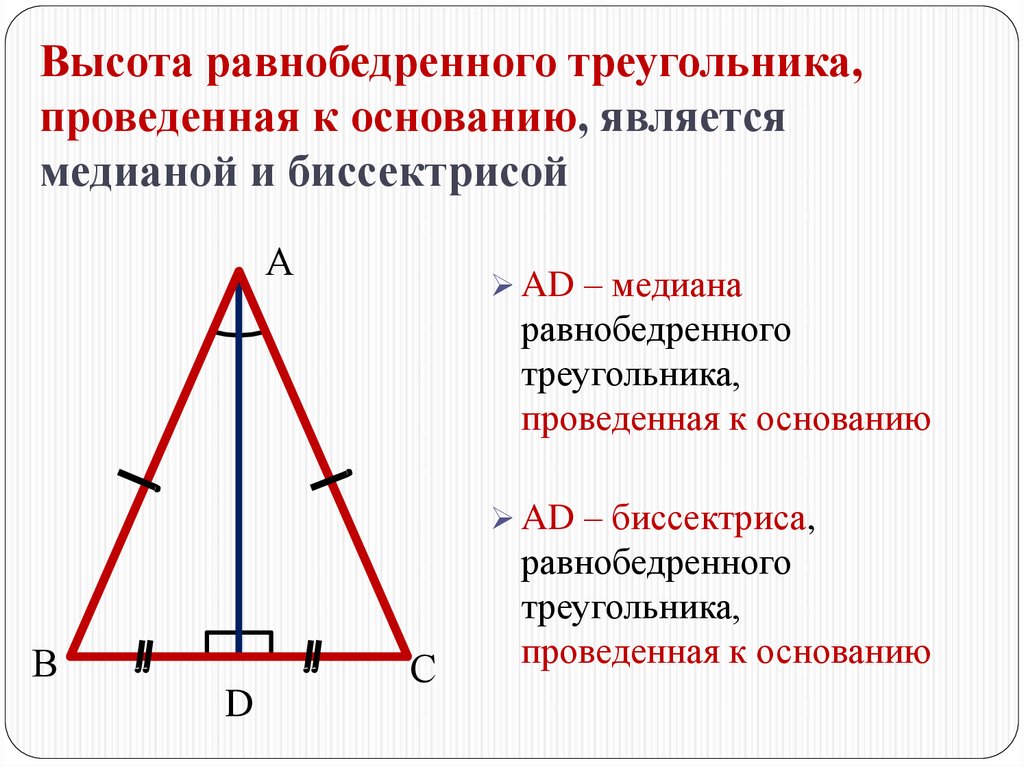
Высота, проведенная к основанию равнобедренного треугольника, также является медианой и биссектрисой.

7 класс, 18 урок, Свойства равнобедренного треугольника
Для нахождения площади используйте формулу: S = (основание × высота) / 2.
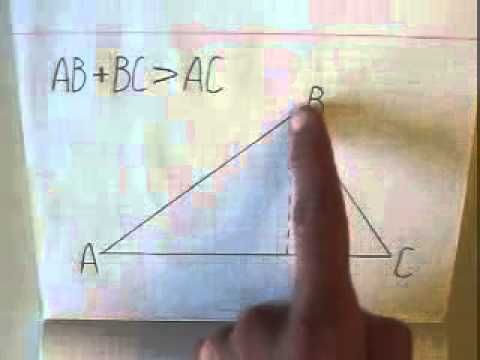
Теорема о соотношении между сторонами треугольника
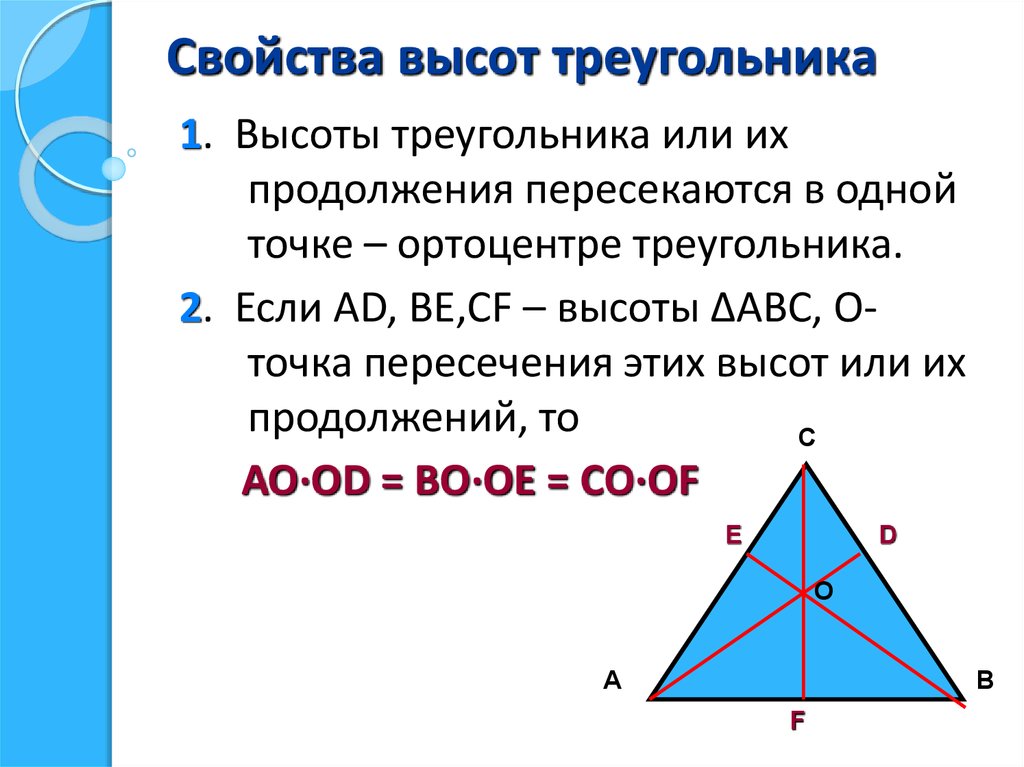
Соотношение сторон можно найти с помощью теоремы Пифагора, если известна высота и основание.

Соотношение между сторонами и углами треугольника
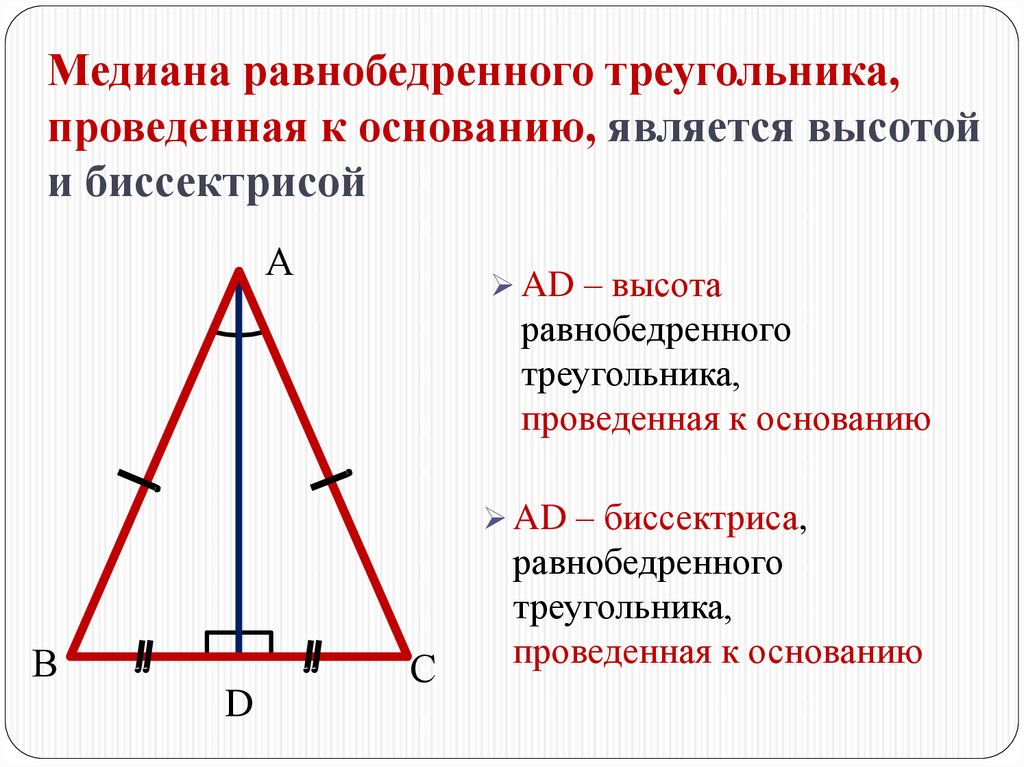
Периметр равнобедренного треугольника равен сумме двух боковых сторон и основания.
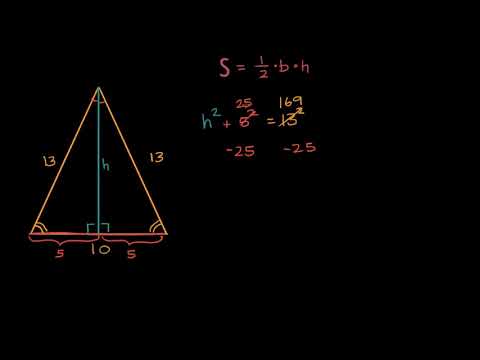
Нахождение площади равнобедренного треугольника при помощи теоремы Пифагора - Геометрия - Алгебра
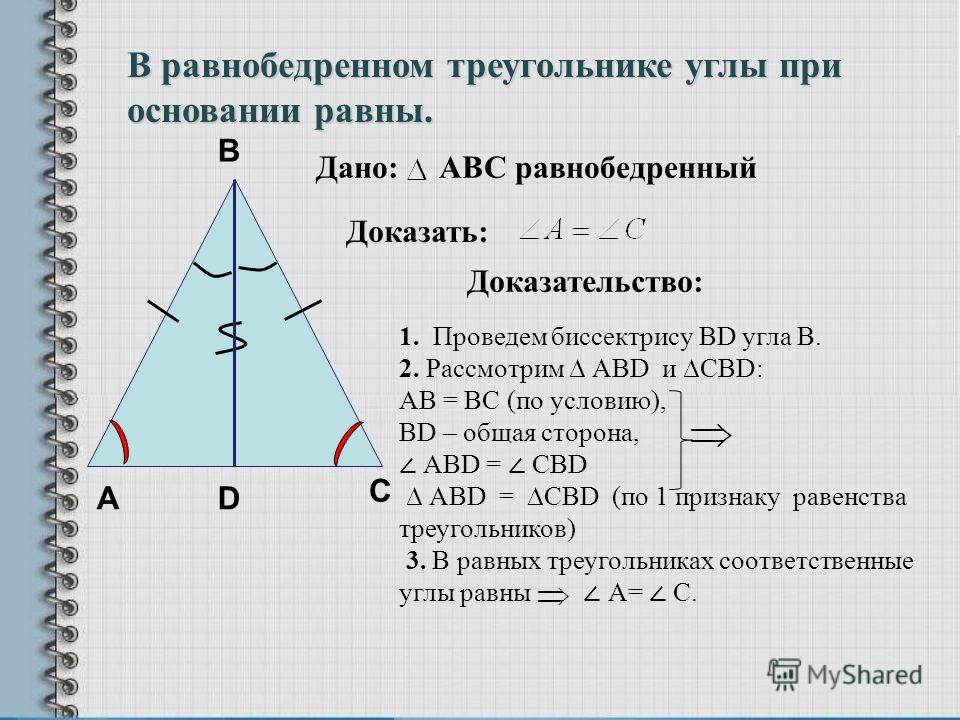
Убедитесь, что сумма длин двух сторон всегда больше длины третьей стороны.

Свойства равнобедренного треугольника #математика #геометрия #рабнобедренныйтреугольник
Если известны углы и одна из сторон, используйте тригонометрические функции для расчета остальных сторон.

Свойства равнобедренного треугольника. 7 класс.

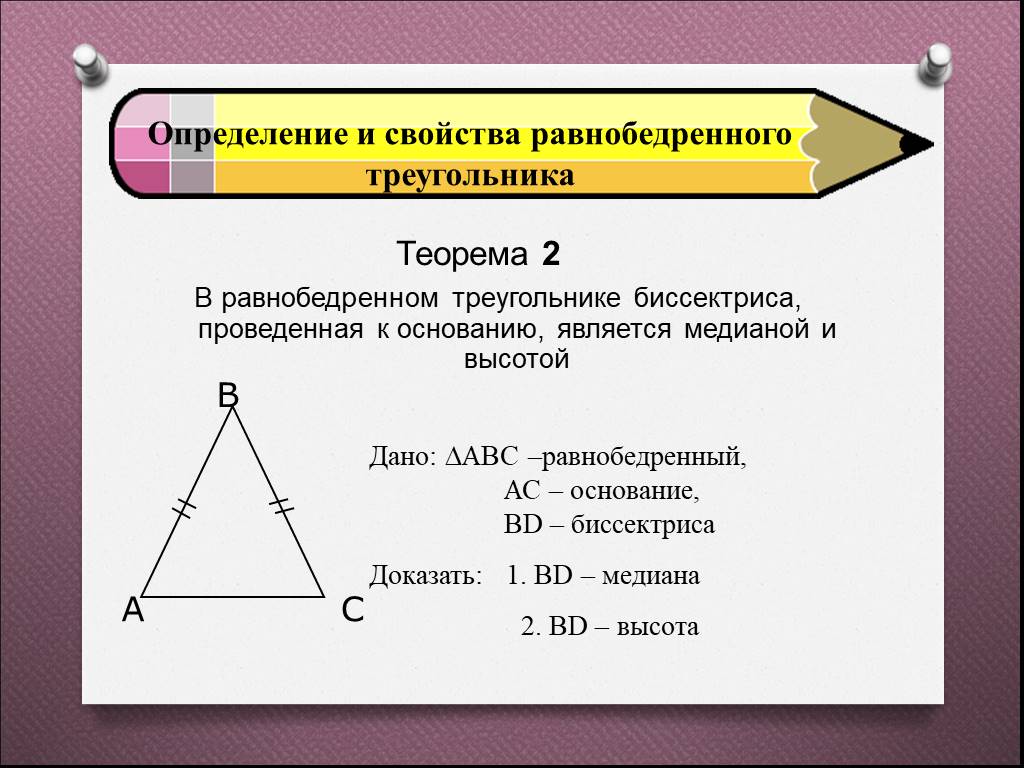
В равнобедренном треугольнике радиус вписанной окружности можно найти по формуле: r = S / p, где p — полупериметр.

Равнобедренный треугольник. Свойства равнобедренного треугольника - Математика - TutorOnline

Для равнобедренных треугольников с острыми углами высота делит основание пополам.

Используйте свойства симметрии равнобедренного треугольника для упрощения задач на построение.

Математика - Метрические соотношения в прямоугольном треугольнике