Равномерное распределение: свойства, примеры и полезные советы
Случайная величина с равномерным распределением — это одна из базовых концепций теории вероятностей, которая находит применение в статистике, моделировании и анализе данных. На странице вы найдете примеры, разъяснения и полезные советы по работе с этим видом распределения.


Всегда определяйте границы распределения (a и b) для более точного анализа.

Равномерное распределение


Равномерное распределение удобно использовать для моделирования событий с равной вероятностью.

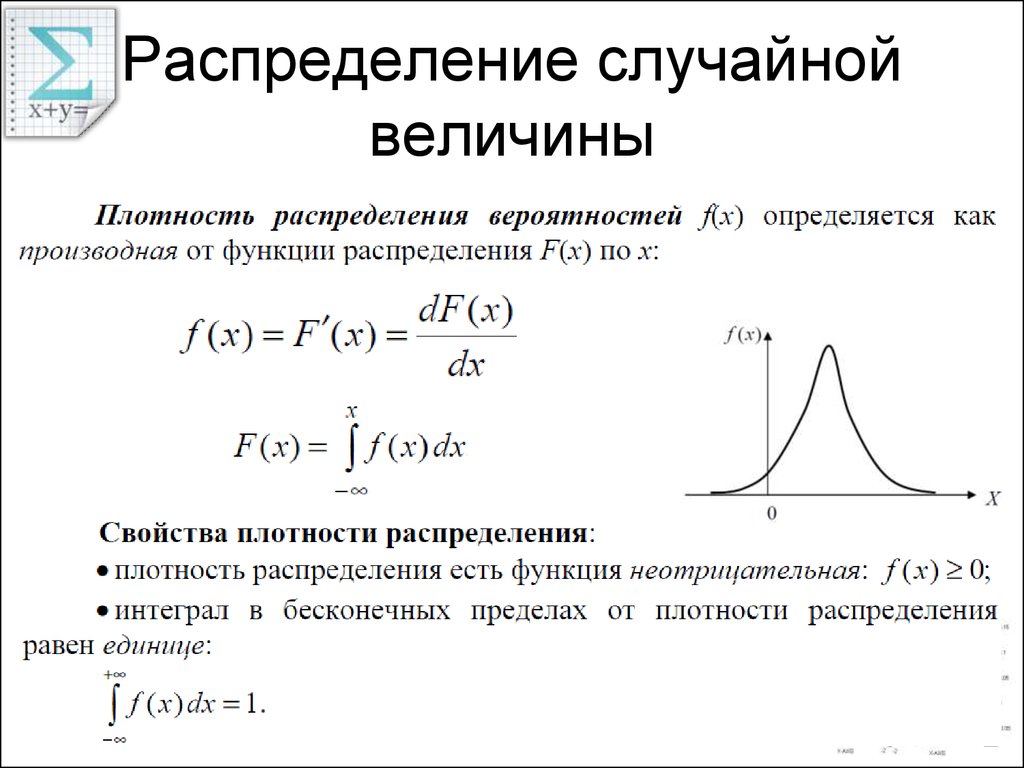
Равномерное распределение непрерывной случайной величины.
Для нахождения вероятности используйте формулу: P(x) = 1 / (b - a), где a ≤ x ≤ b.
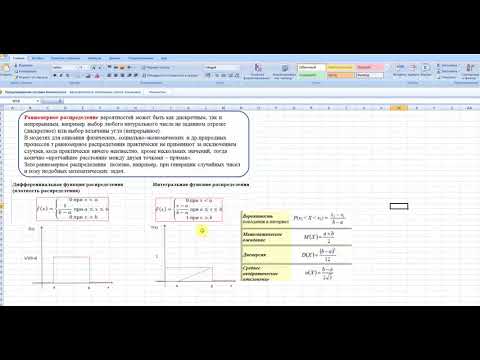
Равномерное распределение

Помните, что математическое ожидание равномерного распределения равно (a + b) / 2.

Нормальное Распределение за 6 Минут


Дисперсия равномерного распределения вычисляется по формуле (b - a)^2 / 12.

Теория вероятностей #12: случайная величина, плотность и функция распределения


Используйте равномерное распределение для генерации случайных чисел в программировании.
Равномерное распределение. Вопросы
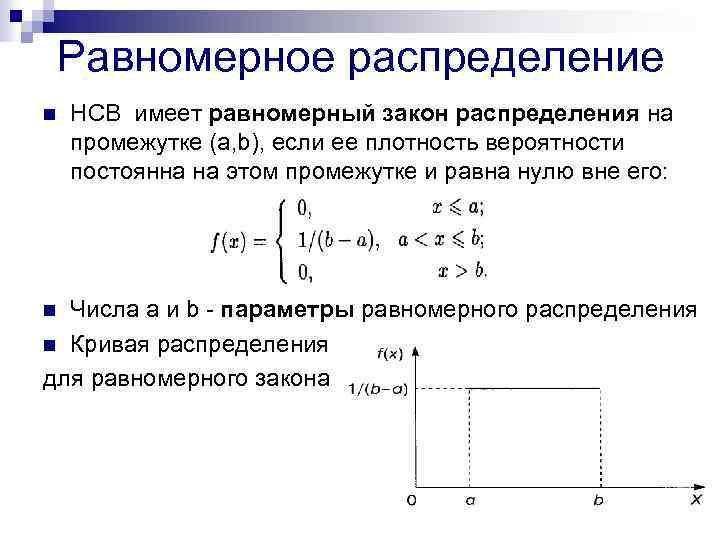
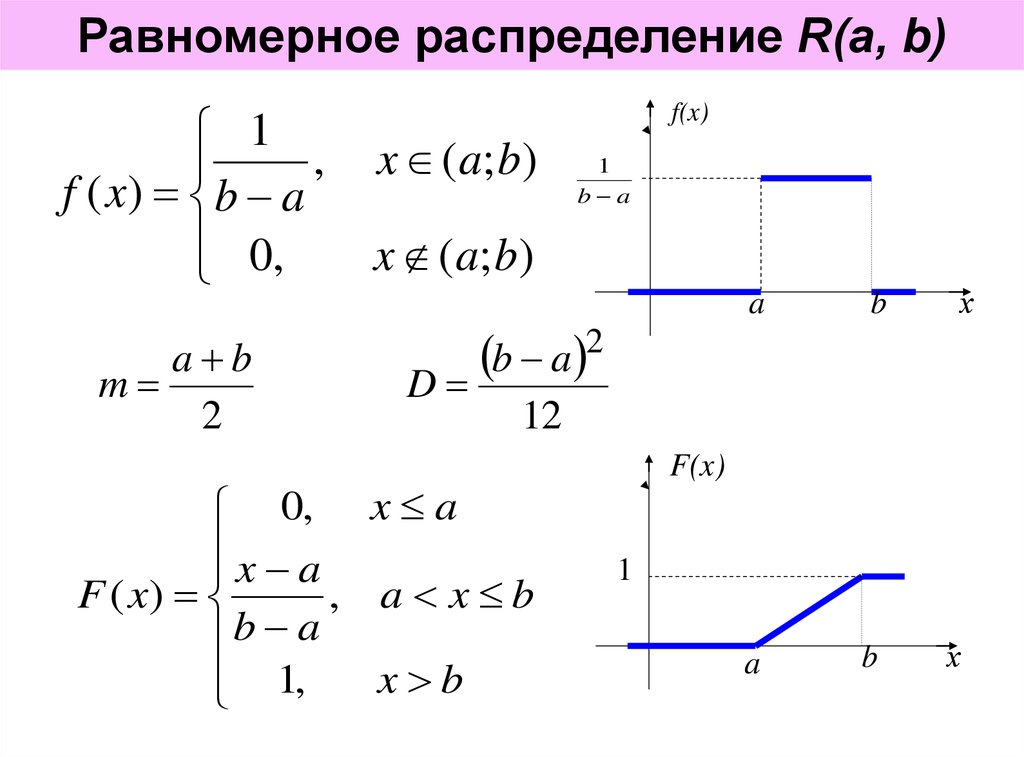
Визуализируйте равномерное распределение с помощью графиков, чтобы лучше понять его свойства.
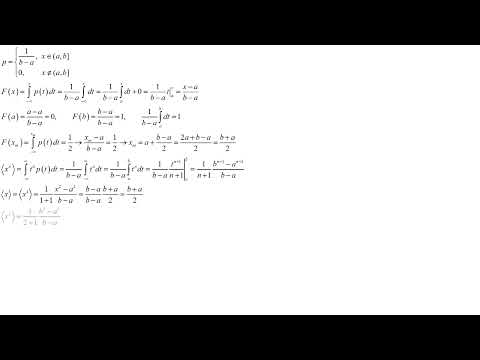
Непрерывное равномерное распределение плотности вероятности


Равномерное распределение применяется в задачах, где нет явных предпочтений одного исхода перед другим.
Равномерное распределение случайной величины
Для сложных расчетов используйте специализированные программные средства, такие как Python или R.

3.2 М.О. Примеры: Распределение Бернулли, равномерное распределение, симметричная случайная величин

Знание свойств равномерного распределения поможет в изучении более сложных видов распределений.
Равномерное распределение. Тема