Как использовать синус угла для решения задач на треугольники
Синус угла — важное понятие в геометрии и тригонометрии. В этой статье вы найдете подборку фотографий и полезных советов для лучшего понимания этой темы.
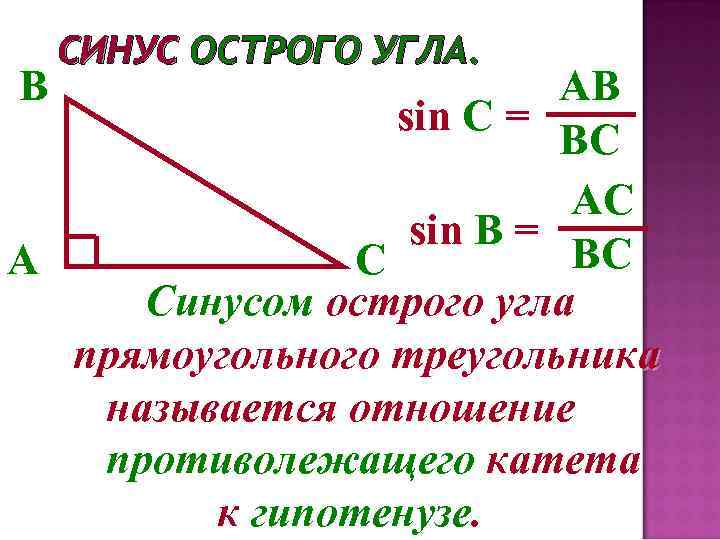
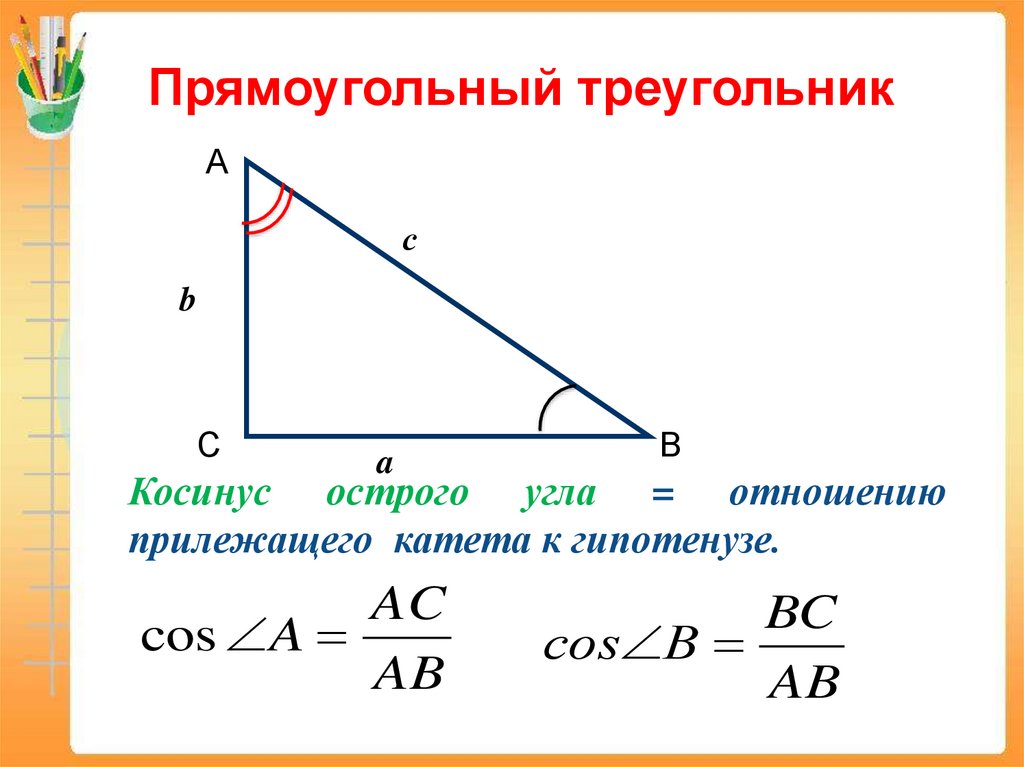
Синус угла определяется как отношение противолежащего катета к гипотенузе в прямоугольном треугольнике.

ТРИГОНОМЕТРИЯ - Синус, Косинус, Тангенс, Котангенс

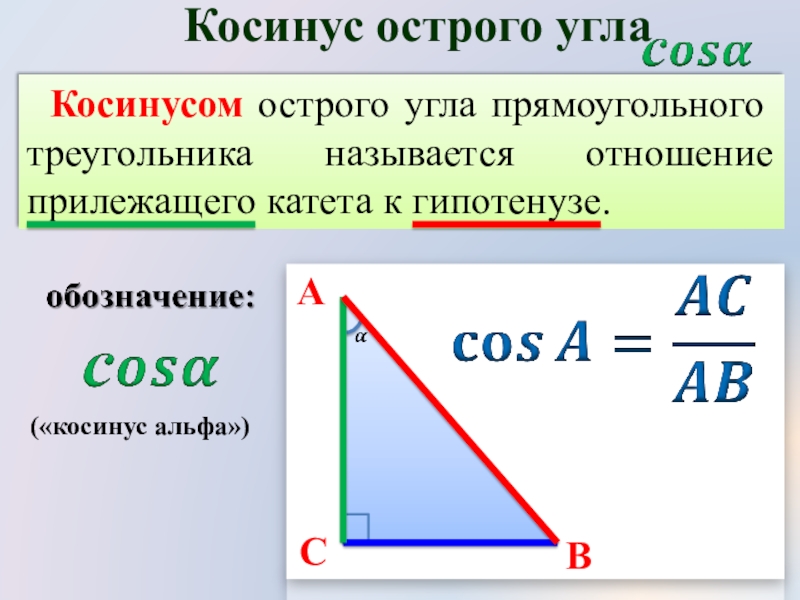
Для вычисления синуса используйте формулу sin(α) = a/c, где a — противолежащий катет, а c — гипотенуза.
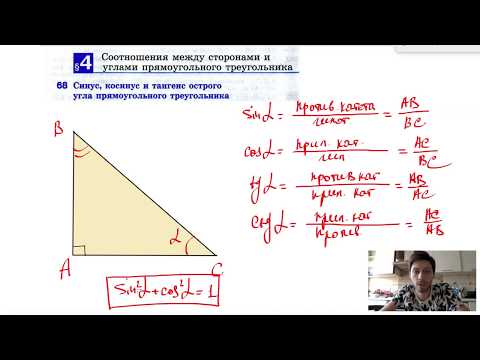
68. Синус, косинус и тангенс острого угла прямоугольного треугольника

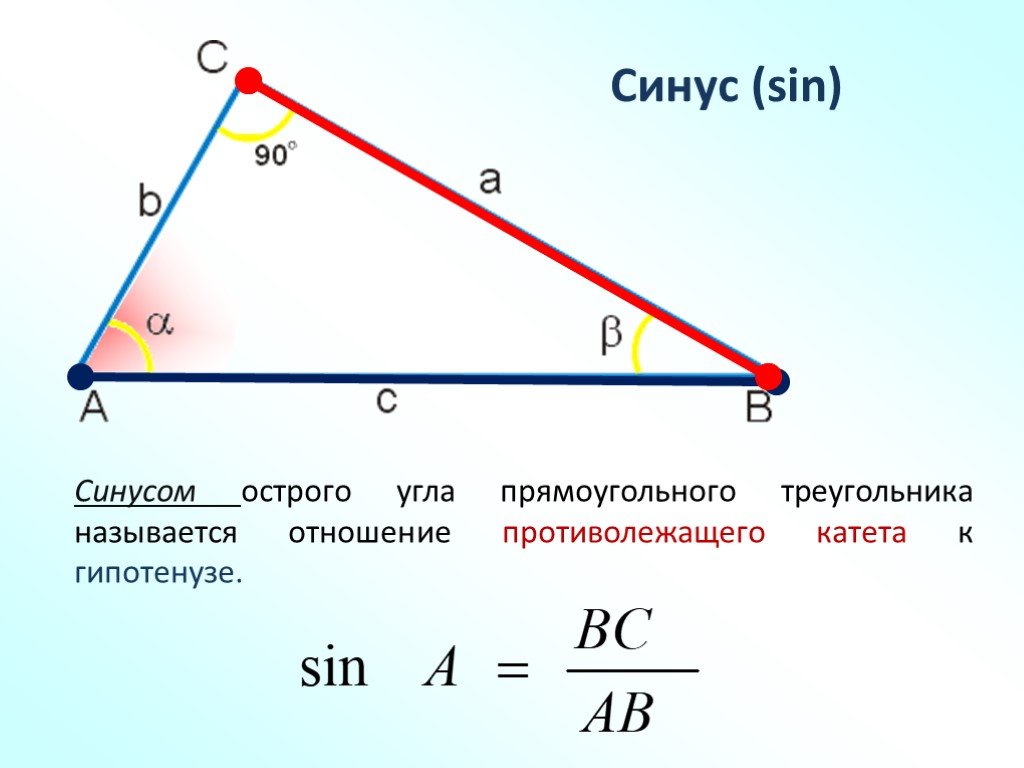
Если угол известен, значение синуса можно найти в таблице или с помощью калькулятора.

Синус, косинус, тангенс, котангенс за 5 МИНУТ


При решении задач обязательно проверяйте, правильно ли определены стороны треугольника.

Задание 9 Прямоугольный треугольник Синус Косинус
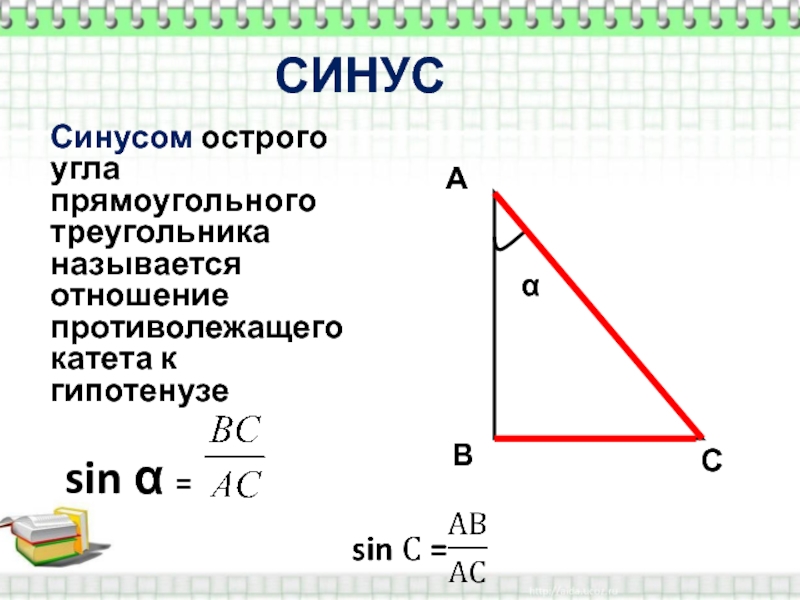

Помните, что синус угла всегда находится в диапазоне от 0 до 1 для острых углов в прямоугольном треугольнике.

Зачем нужны синусы и косинусы?

Используйте тригонометрические функции для нахождения неизвестных сторон или углов треугольника.
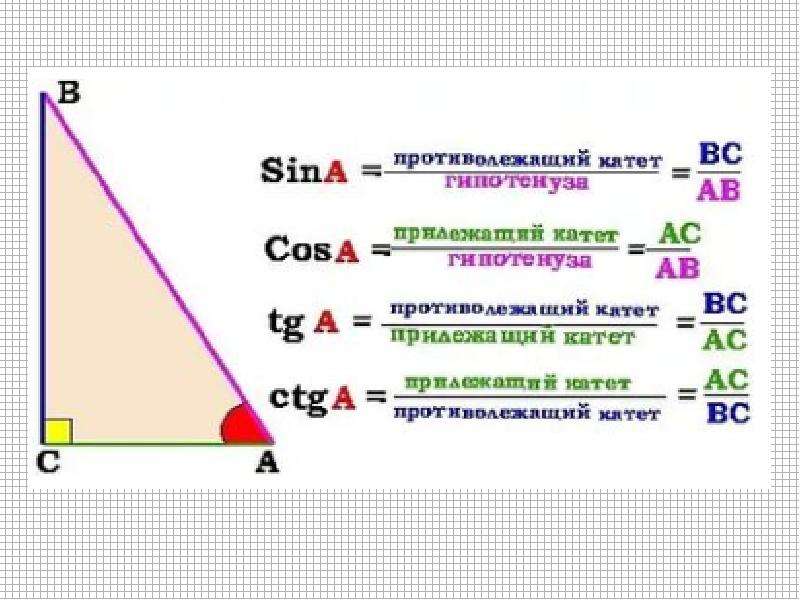
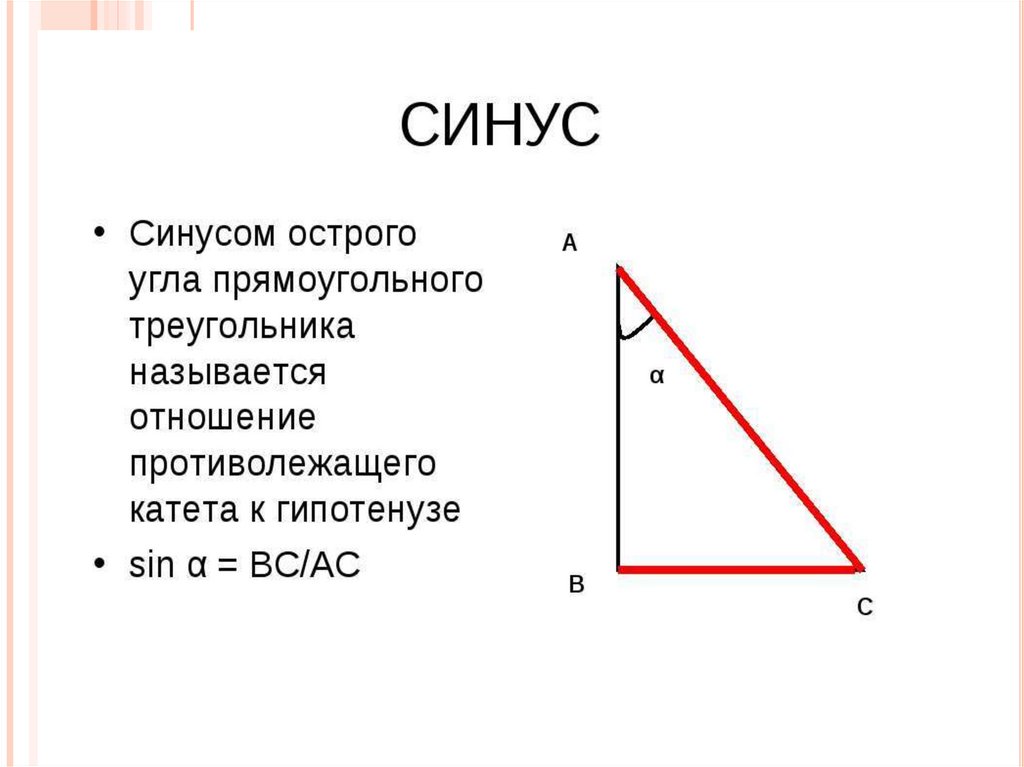
Для практики решайте задачи с использованием синуса на реальных примерах.
Визуализация треугольников и их сторон помогает лучше понять концепцию синуса.

Синус, косинус, тангенс и котангенс в прямоугольном треугольнике.
Запомните основные значения синуса для углов 30°, 45° и 60° для быстрого решения задач.

Геометрия 8. Урок 11- Синус, Косинус, Тангенс и Котангенс угла в прямоугольном треугольнике.

Используйте графики функций для изучения синуса угла и его зависимости от величины угла.
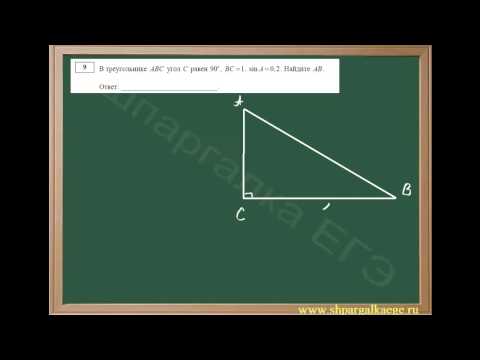
Нахождение стороны прямоугольного треугольника
