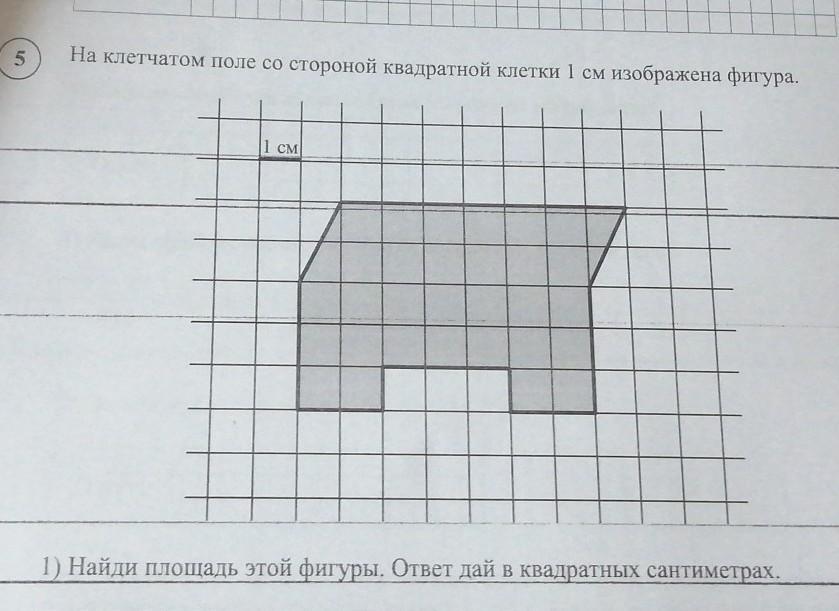
Площадь фигуры по клеточкам с размером стороны 1 см: как это сделать правильно
На этой странице собраны полезные советы и методы вычисления площади различных геометрических фигур, если они изображены на клетчатой бумаге с размером стороны клетки 1 см. Мы расскажем, как быстро и точно определить площадь фигуры, используя простые и доступные подходы.


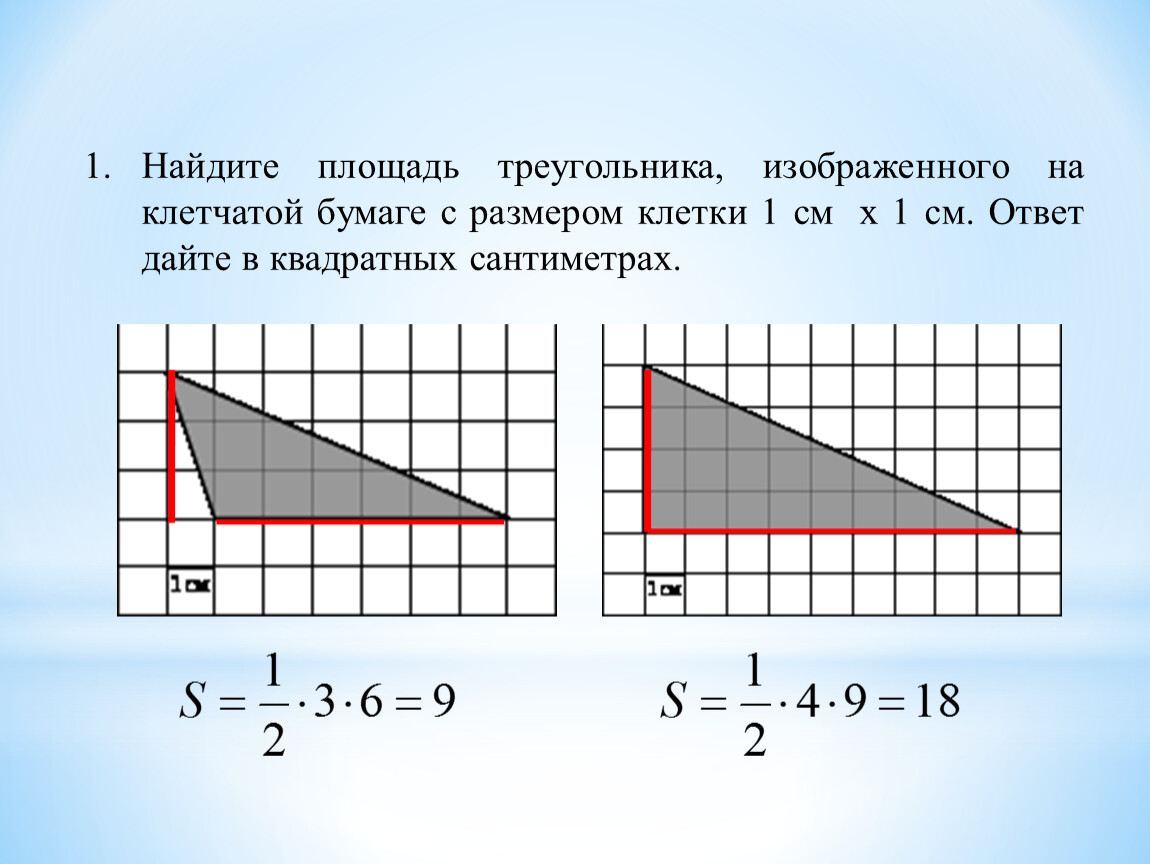
Для правильного подсчета площади фигуры, начните с того, чтобы посчитать количество целых клеточек внутри фигуры.
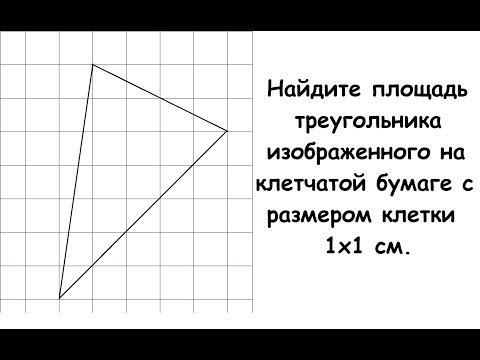
Найдите площадь треугольника изображенного на клетчатой бумаге с размером клетки 1х1 см.


Если фигура имеет сложную форму, разбейте её на более простые части (например, прямоугольники и треугольники), а затем вычислите площадь каждой части.

Самый простой способ нахождения площади
В случае, если часть фигуры попадает на границу клеточек, учитывайте её только в той мере, в какой она полностью охватывает клеточку.

Как найти периметр данной фигуры? Решение за одну минуту!

Если фигура частично покрывает клеточку, используйте подход с дробными частями, например, если клеточка занята на половину — учитывайте её как 0,5.
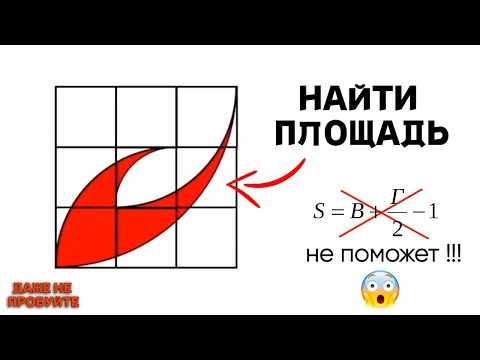
Найти площадь фигуры - Даже не пробуйте

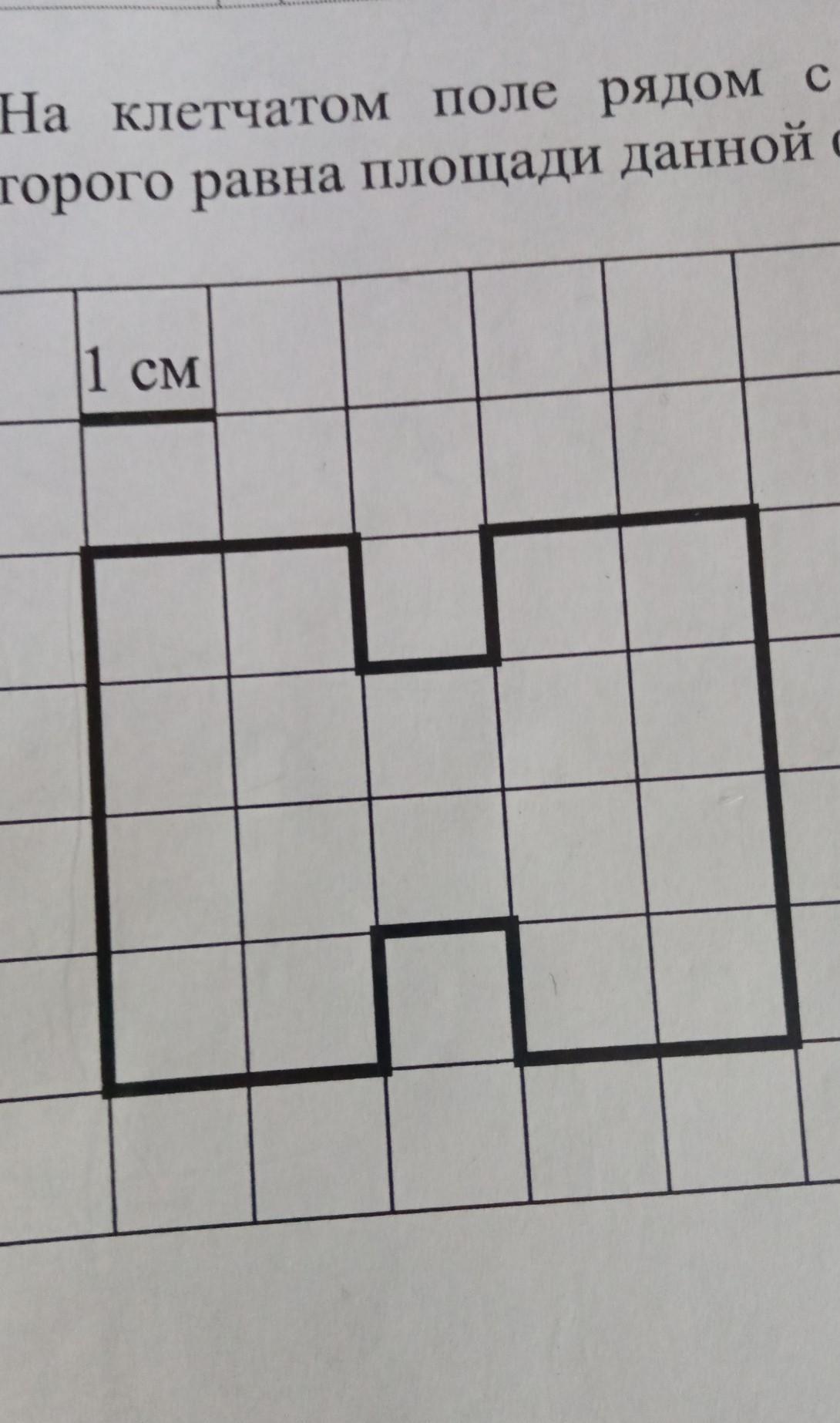
Для более точных вычислений можно использовать метод подсчета клеточек по периметру, чтобы определить площадь по краям фигуры.

Найдите площадь треугольника на рисунке ★ Два способа решения


Помните, что площадь фигуры, изображенной на клетчатой бумаге, измеряется в квадратных сантиметрах, если размер клетки 1 см.

Площадь фигуры
Для вычислений с использованием клеток используйте геометрические формулы для простых фигур и адаптируйте их под клетчатую сетку.
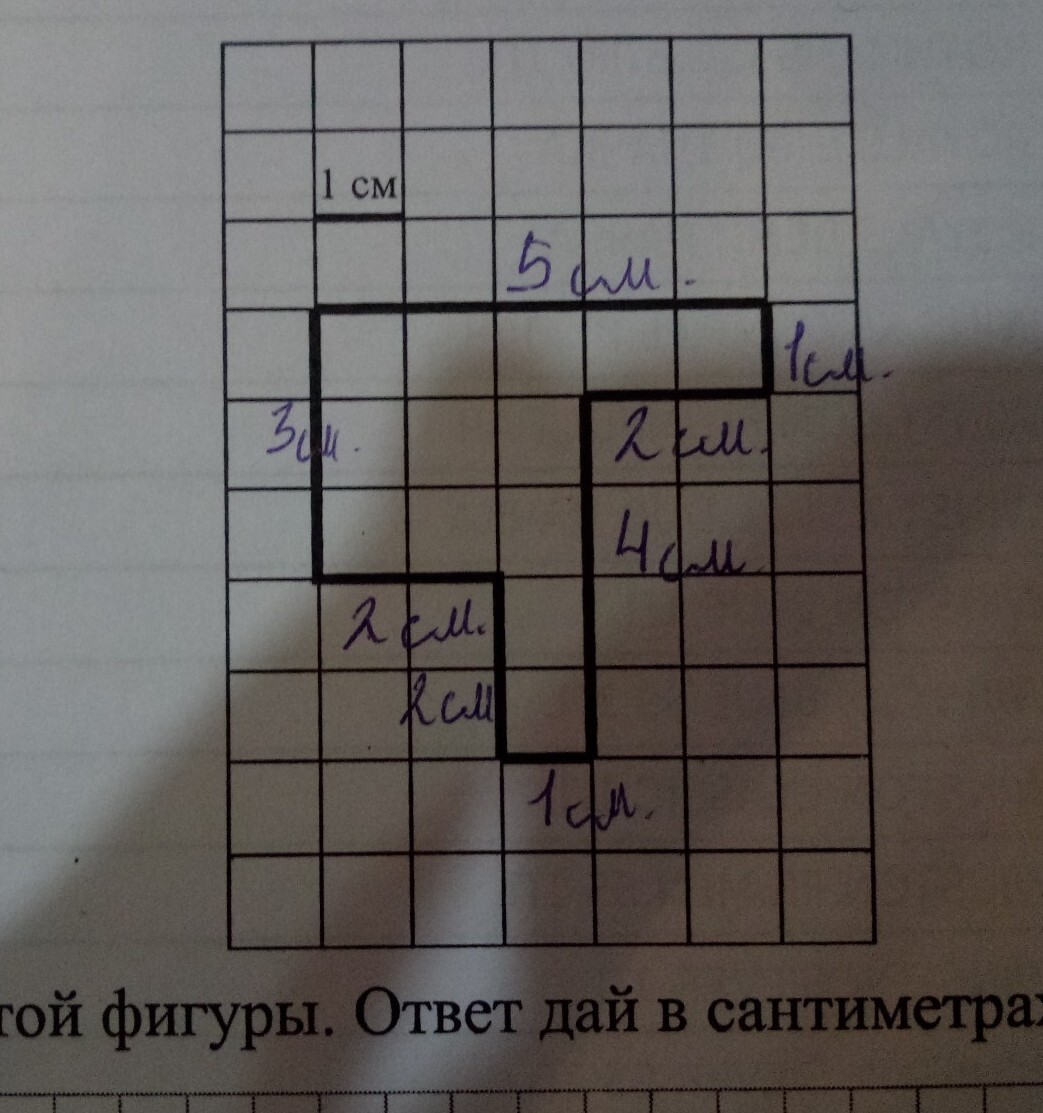
Старайтесь избегать ошибок при подсчете, особенно если фигура близка к границе клеточек. Это может привести к неточным результатам.
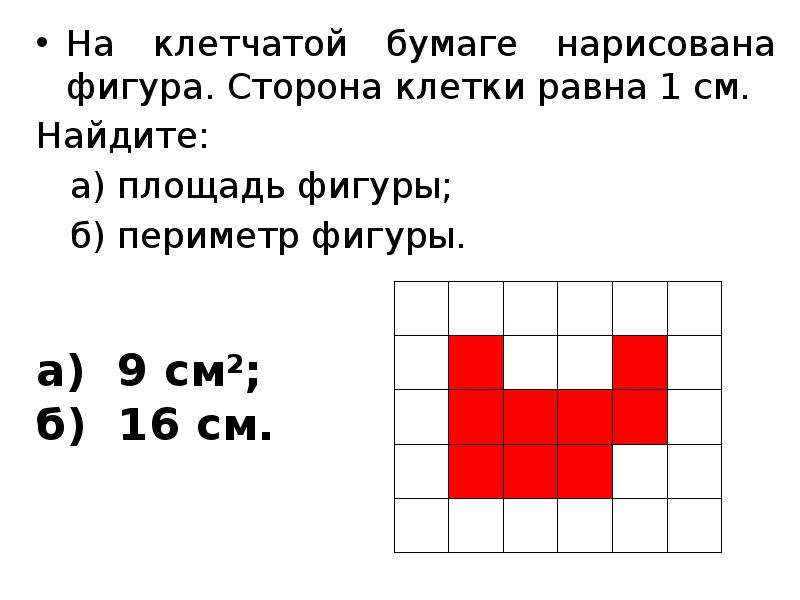
При сложных фигурах, если их невозможно точно разделить на прямоугольники и треугольники, используйте методы аппроксимации площади.
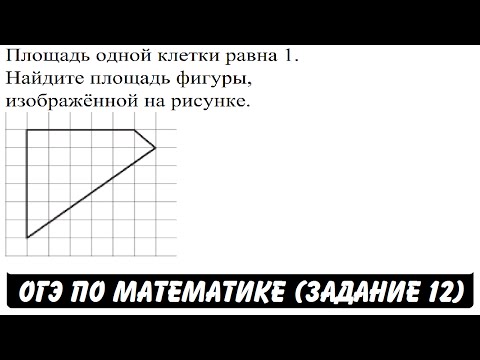
Площадь одной клетки равна 1. Найдите площадь фигуры ... - ОГЭ 2017 - ЗАДАНИЕ 12 - ШКОЛА ПИФАГОРА
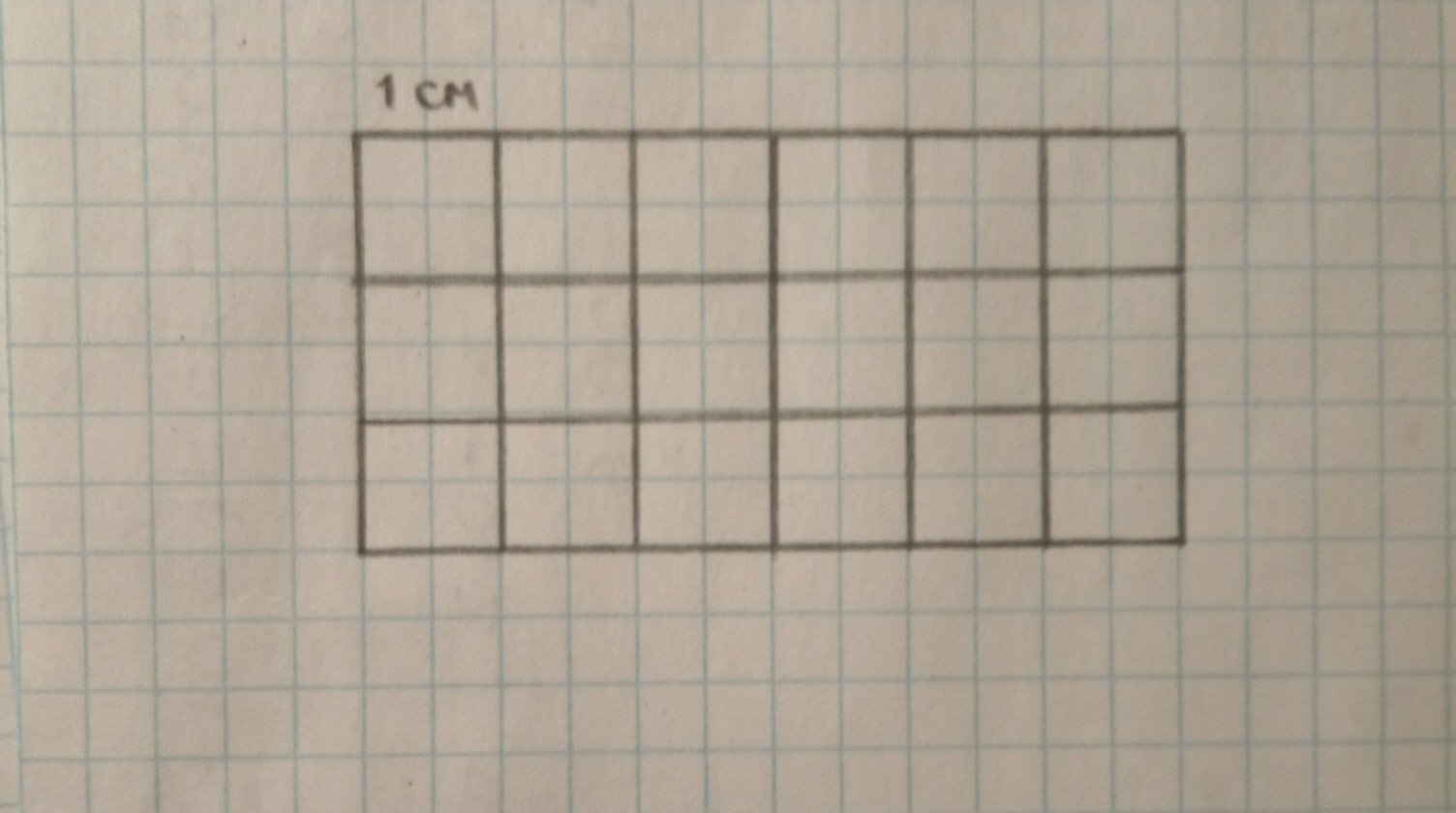
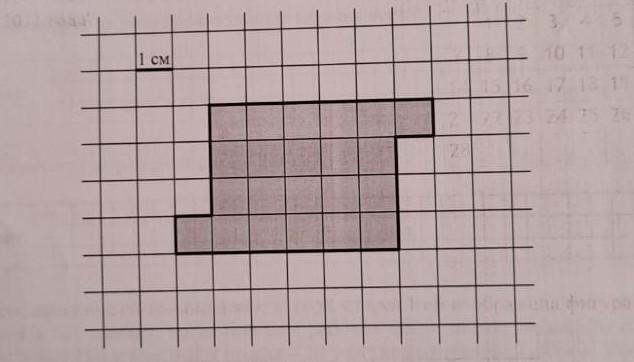
Не забывайте проверять результаты с помощью разных методов — это поможет избежать ошибок и подтвердить точность расчетов.